4.2.1. Представление ХТС в виде графов, матриц и таблиц.
Структуру ХТС обычно рассматривают в терминах теории графов, т.е. в виде ориентированного графа, вершины которого соответствуют аппаратам, а дуги – потокам (например, так как на Рис.4.2). На Рис.4.2 номера вершин обозначены большим курсивом (справа сверху от вершины), а номера потоков – малым прямым шрифтом (под линией соответствующего потока).
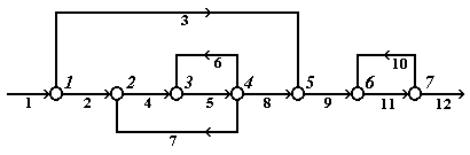
Рис.4.2. Представление ХТС в виде ориентированного графа
Последовательность сцепленных дуг, позволяющая пройти от одной вершины к другой, называется путем. Путь можно обозначить как через последовательность дуг, так и через последовательность вершин. Путь, начальная вершина которого совпадает с конечной, причем каждая вершина, за исключением начальной, проходится только один раз, называется контуром. Например, на Рис.4.2 имеются три контура (по вершинам): 2-3-4-2, 3-4-3 и 6-7-6.
Комплексом, называется часть графа, вершины которого обладают следующими свойствами:
- каждая из вершин и дуг комплекса входит в один из контуров графа;
- если вершина i входит в комплекс, то в этот комплекс входят также все вершины, входящие в контуры, которые содержат вершину i.
Например, на графе, представленном на Рис.4.2 имеются два комплекса (по вершинам): 2-3-4 и 6-7. В первый комплекс входят два контура (2-3-4-2 и 3-4-3), а во второй – один (6-7-6).
Представленная на Рис.4.2 схема движения материальных потоков (граф) является достаточно простой, и, поэтому позволяет проводить свой анализ без применения каких либо программных продуктов. В случае более сложной схемы, проводить анализ становится затруднительно, т.к. при поиске оптимального множества разрываемых потоков комплексов необходимо проводить анализ достаточно большого количества информации и быстродействия. При использовании для анализа структуры ХТС специальных алгоритмов возникает проблема ввода в компьютер структурной схемы, т.е. ее формализация в каком либо числовом виде. В зависимости от выбранного способа анализа, структуру ХТС обычно формализуют в виде матрицы смежности или в виде списка смежности.
Матрица смежности представляет собой двоичную таблицу, количество строк и столбцов которой равны количеству вершин графа. Для учета входных и выходных потоков матрицу смежности добавляют нулевой строкой и столбцом, учитывая как нулевую вершину – окружающую среду. В случае если между двумя вершинами есть связь, то элементу матрицы смежности, находящемся на пересечении столбца и строки с соответствующими номерами вершин, присваивается значение "1", а в случае отсутствия связи – "0". Например, для графа, представленного на Рис.4.2 можно составить следующую матрицу смежности:
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
4 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
7 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
Рис.4.3. Матрица смежности
Список смежности для графа, представленного на Рис.4.2 можно представить в виде:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0 | 1 | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 7 | 6 | 7 |
| 1 | 2 | 5 | 3 | 4 | 3 | 2 | 5 | 6 | 6 | 7 | 0 |
Рис.4.4. Список смежности
В данном списке, первая строка матрицы обозначает номер связи графа. Во второй строке указывается номер вершины, откуда указанная связь выходит, а в третьей – в какую вершину графа связь входит.
Кроме списка смежности, связи графа можно представить в таблицах связей. Например, для графа, представленного на Рис.4.2 таблицы связей будут выглядеть следующим образом:
| Таблица А | Таблица В | ||||||||
1 | 2 | 5 | 1 | 0 | |||||
2 | 3 | 2 | 1 | 4 | |||||
3 | 4 | 3 | 2 | 4 | |||||
4 | 2 | 3 | 5 | 4 | 3 | ||||
5 | 6 | 5 | 1 | 4 | |||||
6 | 7 | 6 | 5 | 7 | |||||
7 | 6 | 7 | 6 | ||||||
Рис.4.5. Таблицы связей
Таблица А называется таблицей входных связей, в таблицу В – таблицу выходных связей. В первом столбце таблицы А указываются все вершины графа, а в последующих – номера вершин графа, куда идут связи из соответствующих номеров вершин, указанных в первом столбце таблицы. В таблице В указываются номера вершин графа, откуда идут связи в соответствующие номера вершин, указанные в первом столбце таблицы В.
Модификацией А и В таблиц связи являются NA и NB таблицы связей, отличающихся от А и В таблиц тем, что в них указываются номера входящих и выходящих в заданную вершину связей:
| Таблица NА | Таблица NВ | ||||||||
1 | 2 | 3 | 1 | 1 | |||||
2 | 4 | 2 | 2 | 7 | |||||
3 | 5 | 3 | 4 | 6 | |||||
4 | 6 | 7 | 8 | 4 | 5 | ||||
5 | 9 | 5 | 3 | 8 | |||||
6 | 11 | 6 | 9 | 10 | |||||
7 | 10 | 12 | 7 | 11 | |||||
Рис.4.6. Модифицированные таблицы связей
Из указанных способов формализации ХТС сложно выбрать один, т.к. все способы одинаково хорошо выполняют свои функции и могут использоваться без каких либо ограничений для формализации и ввода в компьютер структуры ХТС любой сложности. Основным критерием выбора того или иного способа формализации ХТС является выбранный алгоритм поиска оптимального множества разрываемых связей с целью перевода ХТС из замкнутого в разомкнутый вид.


