2.4.6. Определение размера частиц в коллоидных системах оптическим методом
Оптический метод определения размера частиц в «белых» золях, т.е. коллоидных системах не поглощающих свет, основано на использовании уравнения Рэлея (2.2.103). Учитывая, что объемная доля частиц
j = n v1/ V = C /r, (2.2.112)
где n – число частиц в 1 см3 золя или латекса; 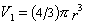 – объем одной сферической частицы; С – массовая концентрация, г/см3;r – плотность полимера, г/cм3; r – радиус частиц, см.
– объем одной сферической частицы; С – массовая концентрация, г/см3;r – плотность полимера, г/cм3; r – радиус частиц, см.
Из уравнения Рэлея можем получить
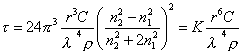 , (2.2.113)
, (2.2.113)
где t– мутность золя (латекса), которую можно измерить с помощью нефелометра, см-1; l – длина волны падающего света, см; n1, n2 – коэффициенты преломления соответственно дисперсионной среды и дисперсной фазы,
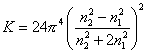 . (2.2.114)
. (2.2.114)
Уравнение (2.2.113) позволяет по измеренной мутности рассчитать радиус частиц, если система подчиняется закону Рэлея для рассеяния света, т.е. при r < l/20.
Часто вместо мутности измеряют оптическую плотность D дисперсной системы. Интенсивность света, проходящего через белый золь, зависит от его рассеяния и выражается уравнением
Iпр.= I0 exp(-t l ) , (2.2.115)
где l – длина рассеивающего слоя, см.
Из уравнения (2.2.115)
t = 2.3 lg( I0/Iпр) / l , (2.2.116)
так как
lg(I0/Iпр) = D, (2.2.117)
то
t = 2,3D/ l , (2.2.118)
для l = 1
t =2,3D. (2.2.119)
Поэтому
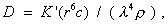 (2.2.120)
(2.2.120)
где
K' = K / 2,3. (2.2.121)
Измерение мутности разбавленного белого золя проводят на нефелометре, а оптической плотности - на фотоколориметре. Иногда шкала фотоколориметра бывает отградуирована как в единицах мутности, так и в единицах оптической плотности.
Если радиус частиц больше l /20, то светорассеяние в таком золе не подчиняется уравнению Рэлея. Это выражается в том, что показатель степени при длине волны падающего света будет отличаться от 4.
Тогда используют эмпирическое уравнение Геллера
D = const l-a , (2.2.122)
или в логарифмической форме
lgD=lg (const) – a lgl . (2.2.123)
В уравнении (2.2.123) величина а обычно изменяется от 4 (рэлеевское рассеяние света) до 2 при r »l. Часто для белых золей используют параметр
Z = 8pr/ lср , (2.2.124)
где lср – среднее значение длин волн света, использованных для определения оптической плотности латекса.
Этот параметр зависит от показателя степени при длине волны использованного света a и после экспериментального определения последнего по углу зависимости, описываемой уравнением (2.2.123) находят по таблице величину Z и рассчитывают радиус частиц. Z лежит в пределах от 2 до 8.
Если Z < 2, то можно использовать уравнение Рэлея, а при Z > 8 частицы уже видны в оптический микроскоп. Значения параметра Z и соответствующие ему показатели степени а при длине волны света приведены в табл. 2.1.
Таблица 2.1
а | Z | a | Z | a | Z |
3,812 | 2,0 | 3,121 | 4,5 | 2.533 | 6,5 |
3,868 | 2,5 | 3,060 | 5,0 | 2,457 | 7,0 |
3,573 | 3,0 | 2,807 | 5,5 | 2,379 | 7,5 |
3,436 | 3,5 | 2,659 | 6,0 | 2,329 | 8,0 |
3,284 | 4,0 |
|
Из табл. 2.1 видно, что постоянная а не может быть меньше 2,3 и больше 3,9.
В 1946 г. Геллер установил зависимость показателя степени в уравнении (2.2.123) для белых золей от размера частиц, экспериментально определяемого независимым методом. Калибровочная кривая Геллера, которая может быть использована для графического определения радиуса частиц, приведена на рис. 2.18. Для радиуса частиц от 50 до 100 нм калибровочная зависимость имеет линейный вид и может быть описана уравнением
a = 3,1 - 2,16×10-2(r -50). (2.2.125)
Это уравнение справедливо для а = 3,1¸2,0. Для других значений показателя степени а расчет надо проводить с использованием функции Z. Для подавляющего большинства латексов синтетических полимеров радиус частиц более 25 нм, поэтому уравнение Рэлея не может быть использовано. Размер частиц таких латексов можно определить с помощью метода Геллера по результатам определения показателя степени при длине волны в уравнении (2.2.122) с последующим использованием табл. 2.1, калибровочной кривой или уравнения (2.2.125).

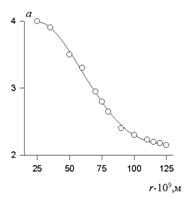 Рис. 2.18. Зависимость показателя степени при длине волны света в уравнении (2.2.122) от размера (радиуса) частиц в белых золях
Рис. 2.18. Зависимость показателя степени при длине волны света в уравнении (2.2.122) от размера (радиуса) частиц в белых золях
