2.3. МОДЕЛЬ САМОСОГЛАСОВАННОГО ПОЛЯ РЕАКЦИИ
В рамках макроскопической теории (шарик с фиксированным распределением зарядов погружен в среду с диэлектрической проницаемостью ε, заряды локализованы внутри шарика) энергия взаимодействия с растворителем задается электростатическим классическим потенциалом
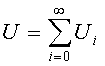, где U0=(q2/2α)(1– 1/ε); U1=(μ2/2α3)[2(ε
– 1)/(2ε + 1)]
и т.д. Здесь q, μ и α - заряд, дипольный момент и радиус шарика соответственно. Первый член этого ряда называют борновским, второй - онзагеровским. Следующие члены ряда зависят от квадрупольного и более высоких мультипольных моментов шарика. Для электрически нейтральных шариков Uo=0 и первым ненулевым членом ряда будет U1. В работах Тапиа с сотр. [88 - 92] предложено добавить аналог члена U1 к гамильтониану изолированной молекулы и учесть таким способом взаимодействие с растворителем. В результате ими было получено следующее выражение для вычисления гамильтониана молекулы, находящейся в растворителе:
Ĥ=Ĥ0 -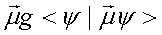
где g- тензор, который определяется восприимчивостью электростатического поля молекулы средой. В работах [88 - 92] он задавался в параметрической форме.
Этот метод учета взаимодействия с растворителем получил название модели самосогласованного поля реакции. Основные его недостатки очевидны. Они заключаются в необходимости учета зависимости тензора g от значения диэлектрической проницаемости растворителя и размеров молекулы. Это нельзя сделать без очень грубых дополнительных предложений. Обычно полагают, что диагональные элементы g равны 2(ε - 1)/[(2ε + 1)α3], а недиагональные - нулю. Однако перенесение макроскопической формулы на микроскопический уровень, вообще говоря, неверно, диэлектрическая проницаемость при этом теряет свой физический смысл, а выбор значения параметра α (радиуса молекулы) достаточно произволен. Поэтому модель самосогласованного поля реакции имеет ограниченную область применения. Практически ею можно пользоваться при рассмотрении реакций изомеризации и переноса протона. В остальных случаях ее использование нежелательно.