9.3. Стационарная теплопроводность через цилиндрическую стенку

1). Однородная цилиндрическая стенка.

Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d₁и внешним диаметром d₂ (Рис.9.4).



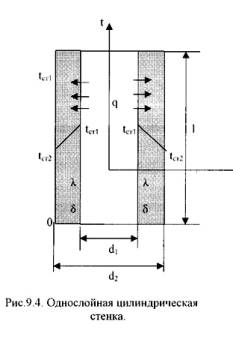
Температуры поверхностей стенки –t_ст1 и t_ст2.

Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = - λ∙2∙π∙r ·l· ∂t / ∂r (9.24)илиQ = 2·π·λ·l·Δt/ln(d₂/d₁), (9.25)где: Δt = t_ст1 – t_ст2 – температурный напор;

λ – κоэффициент теплопроводности стенки.

Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:q_l = Q/l =2·π·λ·Δt /ln(d₂/d₁), [Вт/м]. (9.26)Температура тела внутри стенки с координатойd_х:t_x = t_ст1 – (t_ст1 – t_ст2) ·ln(d_x/d₁) / ln(d₂/d₁). (9.27)2). Многослойная цилиндрическая стенка.

Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5).



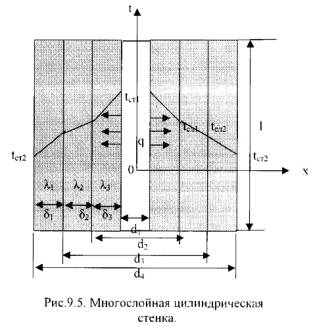
Температура внутренней поверхности стенки –t_ст1, температуранаружнойповерхности стенки –t_ст2, коэффициенты теплопроводности слоев -λ₁, λ₂, λ₃, диаметры слоев d₁, d₂, d₃, d₄.

Тепловые потоки для слоев будут:

1-й слойQ = 2·π· λ₁·l·(t_ст1 – t_сл1)/ ln(d₂/d₁), (9.28)

2-й слой

Q = 2·π·λ₂·l·(t_сл1 – t_сл2)/ ln(d₃/d₂), (9.29)

3-й слой

Q = 2·π·λ₃·l·(t_сл2 – t_ст2)/ ln(d₄/d₃), (9.30)Решая полученные уравнения, получаем для теплового потока через многослойную стенку:Q = 2·π·l·(t_ст1 – t_ст2) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (9.31)Для линейной плотности теплового потока имеем:q_l = Q/l = 2·π· (t₁ – t₂) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (9.32)Температуру между слоями находим из следующих уравнений:

t_сл1 = t_ст1 – q_l·ln(d₂/d₁) / 2·π·λ₁ . (9.33)

t_сл2 = t_сл1 – q_l·ln(d₃/d₂) / 2·π·λ₂ . (9.34)

Предыдущая страница | Следующая страница

СОДЕРЖАНИЕ