Концентрационная коагуляция

Рассмотрим изменение энергии взаимодействия частиц при добавлении электролитов, предполагая, что постоянная сил межмолекулярного притяжения (постоянная Гамакера) и потенциал на плоскости Штерна j_s остаются неизменными при добавлении электролитов к дисперсной системе. Для простоты ограничимся также рассмотрением случая, когда r>>k^-1, т.е. будем рассматривать потенциальную энергию взаимодействия плоских частиц.

С увеличением содержания электролита в системе высотамаксимума на кривой зависимости потенциальной энергии взаимодействия частиц от расстояния между ними будет снижаться. Дляустойчивой системы без добавок электролита характерным является потенциальная энергия взаимодействия, соответствующаялинии 1 на рис. 2.23. Если между частицами не будет даже малейших сил отталкивания, то таким системам присуща зависимость потенциальной энергии взаимодействия, описываемая кривой 3.

Условиями начала коагуляции будут

U_t = U_e+ U_m= 0 (2.3.122)

и

(dU_e/dh) + (dU_m/dh) = 0, (2.3.123)

или

(h d lnU_e/dh) = [d ln(-U_m) / d lnh]. (2.3.124)

Этому условию на рис. 2.23 соответствует кривая 2, у которой максимум соответствует U=0. Очевидно, что первое условие возможно при равенстве энергий притяжения и отталкивания на некотором расстоянии, соответствующем критической толщине прослойки между частицами (h_c).

Используя для описания энергии отталкивания уравнение (2.3.41), а для энергии притяжения уравнение (2.3.21), можем записать условие равновесия энергий отталкивания и притяжения плоских частиц через прослойку толщиной h_c раствора электролита с концентрацией С_с:

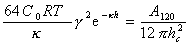(2.3.125)

и

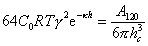, (2.3126)

где g описывается уравнением (2.3.42)

Из этих уравнений с учетом уравнения (2.3.124) следует, что

kh_c» 2. (2.3.127)

Очевидно, что снижение толщины диффузионной оболочки при введении электролитов, способное привести к соотношению (2.3.127), вызовет процесс коагуляции. С учетом уравнения (2.3.38) из уравнения (2.3.126) получаем выражение для порога коагуляции сильно заряженных частиц, когда zFj_s>>2RT,

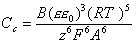, (2.3.128)

где В – постоянная, слабо зависящая от валентности побочного иона, но зависящая от формы частиц.

Уравнение (2.3.128), известное как «закон валентности» коагулирующих ионов, было получено Дерягиным и Ландау. Это уравнение можно записать в форме

С_с = сonst / z⁶. (2.3.129)

Уравнение (2.3.129) дает теоретическое обоснование известным правилам электролитной коагуляции Шульце – Гарди.

Для слабо заряженных частиц критерий коагуляции имеет вид

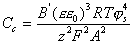, (2.3.130)

где постоянная В' » 0,42.

Из уравнения (2.3.130) видно, что для коагуляции слабо заряженных частиц получается закон «z²»:

С_с = сonst / z². (2.3.131)

Как показал И. Ф. Ефремов, если соблюдается это уравнение, то можно с уверенностью утверждать, что происходит процесс коагуляции с фиксированием частиц во втором потенциальном минимуме. Это, как правило, приводит к формированию пространственной коагуляционной структуры.

Критериальные уравнения (2.3.128) и (2.3.120) можно применять для процесса концентрационной коагуляции, когда в присутствии электролитов сжимается диффузионная обкладка двойного электрического слоя, но потенциал поверхности частиц остается неизменным.

Из приведенных выше уравнений следует, что коагуляция - процесс необратимого нарушения агрегативной устойчивости - происходит при введении электролитов вплоть до критической концентрации, называемой порогом коагуляции, когда вследствие сжатия диффузных оболочек двойного электрического слоя частиц до некоторой критической толщины энергия отталкивания частиц уравняется с энергией притяжения. После этого любое столкновение частиц приводит к их слипанию, а формирование больших агрегатов первичных частиц приводит к выпадению дисперсной фазы в осадок, т.е. нарушается и кинетическая устойчивость.