Гетерокоагуляция
Для вывода критериальных уравнений коагуляции сферических частиц одинакового или различного размера с различными потенциалами поверхности или для процесса нарушения устойчивости дисперсных систем вблизи бесконечной плоской поверхности поступают аналогичным описанному выше образом, т.е. приравнивают полную энергию взаимодействия нулю и находят производную полной энергии взаимодействия по расстоянию между частицами в точке Uh = 0.
В случае нарушения устойчивости в результате подавления энергии отталкивания сферических частиц различного размера с различным потенциалом поверхности при введении электролитов в дисперсные системы говорят о процессе гетерокоагуляции. Процесс осаждения частиц дисперсной фазы на бесконечной поверхности при нарушении агрегативной устойчивости дисперсий в результате введения электролитов называют гетероадагуляцией.
Если в смешанных дисперсных системах присутствуют частицы, по крайней мере, двух типов и энергия межмолекулярного взаимодействия вызывает их притяжение, то говорить об агрегативной устойчивости таких систем можно только в том случае, когда частицы имеют хотя бы и различный по величине, но одинаковый по знаку поверхностный потенциал. Если частицы несут на своей поверхности различный по знаку заряд, то электростатическое притяжение и межмолекулярное взаимодействие незамедлительно вслед за смешением двух дисперсных систем с различными частицами приведут к гетерокоагуляции. В этом разделе мы будем обсуждать процесс гетерокоагуляции только таких дисперсных систем, в которых у различных частиц знак заряда поверхности одинаковый.
Также как и в случае гомокоагуляции, электролитная гетерокоагуляция может быть двух типов: концентрационная и нейтрализационная. При рассмотрении концентрационной гетерокоагуляции существенную роль играет факт различия величины потенциалов поверхности частиц. Если потенциалы у обеих взаимодействующих частиц высокие, то отличие между ними не может существенно повлиять на условия быстрого слипания и необратимой коагуляции. Для таких систем остается справедливым критериальное уравнение (2.3.128).
В случае если потенциал одной из частиц высокий, а у другой частицы потенциал поверхности мал, критериальное уравнение имеет вид, характерный для частиц с малым потенциалом:
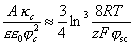. (2.3.134)
Из этого уравнения видно, что для систем с сильно различающимися потенциалами критерий устойчивости напоминает таковой для слабо заряженных частиц с той разницей, что правая часть уравнения (2.3.134) не равна единице. Из этого следует, что критическое значение потенциала поверхности, при котором будет происходить слипание несимметричных частиц, будет меньше, чем у симметричных (при прочих равных условиях).
Если слипание частиц происходит в результате одновременного снижения потенциалов обеих частиц (случай низких потенциалов), то критериальное уравнение имеет вид
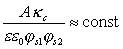, (2.3.135)
где постоянная в правой части уравнения зависит от соотношенияjs1/js2.
Так расчет показывает, что при js1/js2 = 1 из уравнения (2.3.135) следует (kh)c = 2, что характерно для одинаковых частиц. При js1/js2= 5 следует (kh)c = 2,6 , а при js1/js2.= 10 получается (kh)c = 3. Из чего можно заключить, что критическое значение (kh)c слабо зависит от соотношения потенциалов поверхностей слабо заряженных частиц.
Для практических расчетов, проводимых с целью определения критерия устойчивости при гетерокоагуляции и гетероадагуляции, целесообразно осуществлять численный расчет на ЭВМ полной энергии взаимодействия частиц различного размера и с различным потенциалом поверхностей.