4.4. Реологические кривые жидко- и твердообразных структурированных дисперсных систем
При рассмотрении результатов исследования реологических свойств структурированных систем можно выделить два характерных типа полных реологических кривых для систем
- с жидкообразной структурой, у которых течение начинается вслед за приложением напряжения (рис. 2.40);
– с твердообразной структурой, течение которых начинается только после некоторого предельного напряжения (рис. 2.41).
Полные реологические кривые характерны для течения относительно разбавленных растворов полимеров, поверхностных слоев ПАВ, некоторых тиксотропных дисперсий. В таких системах образуются жидкообразные структуры. При постоянном напряжении сдвига, время действия которого больше периода релаксации, устанавливается стационарное течение. При небольшом напряжении сдвига система течет без разрушения структуры с высокой вязкостью h0 (участок 0 – Рs на рис. 2.40). Отмеченное на оси значение Рs, называемое статическим напряжением сдвига, является критическим напряжением, которое необходимо для разрушения структуры, образовавшейся в системе в статических условиях. При этом первом критическом напряжении сдвига начинается частичное обратимое разрушение структуры.
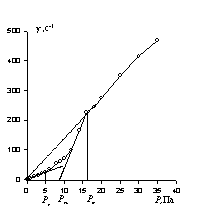
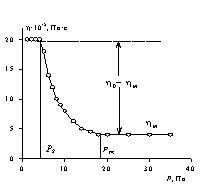
Рис. 2.40. Полные реологические кривые течения жидкообразной структурированной системы
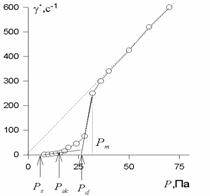
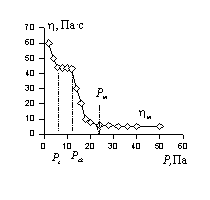
Рис. 2.41. Полные реологические кривые твердообразной структурированной системы |
При напряжении Рsk разрушение структуры завершается. Следовательно, Рsk – то критическое напряжение сдвига, которое необходимо для полного разрушения структуры, образовавшейся в стационарных условиях. Если бы в системе не восстанавливалась обратимо тиксотропная структура, то при Р >Рsk система обладала бы свойствами истинной ньютоновской жидкости.
Однако для течения жидкой структурированной системы часть работы будет расходоваться на разрушение этой тиксотропно восстанавливающейся структуры, а Рm – напряжение, после которого жидкость приобретает свойства ньютоновской жидкости, т.е. то критическое максимальное напряжение, необходимое для полного разрушения структуры, образовавшейся в статических условиях и восстанавливающейся в динамических. Все критические значения напряжения сдвига можно выявить только на полной реологической кривой в координатах «g– Р». При выражении полной реологической кривой в координатах «hef– Р» можно достаточно четко выделить Рs и Рm , т.е. критические значения напряжения начала и завершения разрушения структуры. Можно отметить два значения вязкости: в области напряжений (0 – Рs) – вязкость, эффективная для жидкости с неразрушенной структурой, и в области Р > Рm – вязкость ньютоновской жидкости с полностью разрушенной структурой. В промежуточной области напряжений (Рs - Рm) вязкость монотонно уменьшается от величины h0 до hm.
При достижении критического статического напряжения сдвига Рs, необходимого для разрушения твердообразной структуры, образовавшейся в статических условиях, система начинает необратимо деформироваться, и наблюдается пластическое течение с переменной вязкостью вплоть до напряжений Рd,после чего пластическое течение происходит с постоянным динамическим (тиксотропным) восстановлением структуры. Этот участок кривой описывают уравнением Бингама и говорят о бингамовской вязкости дисперсной системы hmin.
На участке Рsk – Рd эффективная (кажущаяся) вязкость изменяется в очень широких пределах, иногда различие составляет два и более порядка. Участок реологической кривой с постоянной вязкостью hmax характерен для, так называемой, шведовской жидкости, которая характеризуется пластично-вязким течением. Уравнение Шведова для описания этого участка имеет вид
P = Ps + h*max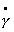 , (2.4.59)
, (2.4.59)
где h*max – пластическая эффективная (шведовская) вязкость. Участок напряжений Рd – Рm характеризуется уравнением Бингама в форме
P = Ps + h*min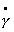 , (2.4.60)
, (2.4.60)
где h*min – пластическая эффективная (бингамовская) вязкость.
Построение полных реологических кривых течения позволяет определить ряд постоянных для описания структурно-механических свойств дисперсных систем.
В области от Рs до Рm эффективная вязкость зависит от доли обратимо (тиксотропно) восстанавливающихся связей между частицами и эта зависимость для жидкообразных структур имеет вид
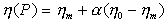 . (2.4.61)
. (2.4.61)
Уравнение (2.4.61) предложил П.А. Ребиндер.
Для твердообразных структур это уравнение будет иметь вид
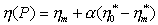 . (2.4.62)
. (2.4.62)
Как показал М. Кросс для жидкообразных структур степень восстановления структуры
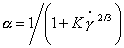 , (2.4.63)
, (2.4.63)
где K = ki / k0 – постоянная относительной скорости разрушения структуры; ki, k0– постоянные скорости разрушения при градиенте скорости, соответственно 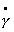 и
и 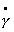 = 0.
= 0.
Уравнение (2.4.61) с учетом уравнения (2.4.63) можно привести к линейной форме, если использовать величину, обратную вязкости, т.е. 1/h, называемую текучестью:
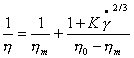 . (2.4.64)
. (2.4.64)
Если hm << h0, то
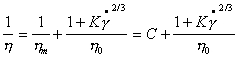 . (2.4.65)
. (2.4.65)
Постоянная С зависит от концентрации растворов, температуры, химической природы и молекулярной массы полимеров.