Релаксация

РЕЛАКСАЦИЯ (от лат. relaxatio-ослабление), процесс установления в системе термодинамического равновесия. Состояние макроскопич. системы определяется мн. параметрами, и процессы достижения равновесия по разным параметрам могут протекать с разл. скоростями. Выделяют период линейной релаксации, когда нек-рый параметр состояния x_i лишь незначительно отличается от своего равновесного значения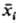. В этот период скорость изменения параметра dx_i/dt пропорциональна величине отклонения х_i от:

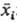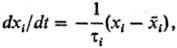
где т_i-время релаксации. Отсюда следует, что в момент времени t отклонение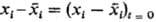ехр (—t/т_i). За время т_i малое отклонение параметра х_i от равновесного значения уменьшается в е раз. Величины v_i = 1/т_i, обратные временам релаксации, наз. частотами релаксации.

Времена релаксации определяются св-вами системы и типом рассматриваемого процесса. В реальных системах они могут варьировать от ничтожно малых величин до значений порядка возраста Вселенной. Система может достигнуть равновесия по одним параметрам и остаться неравновесной по другим (частичное равновесие). Все процессы релаксации являются неравновесными и необратимыми и сопровождаются диссипацией энергии, т.е. в системе производится энтропия (см. Термодинамика необратимых процессов).

В газах релаксация обусловлена обменом энергией и кол-вом движения при столкновениях частиц, а время релаксации определяется временем своб. пробега (среднее время между двумя последоват. столкновениями молекул) и эффективностью обмена энергией между всеми степенями свободы сталкивающихся частиц. В одноатомных газах выделяют этап быстрой релаксации, когда за короткий период времени порядка времени столкновения молекул начальное (сильно неравновесное) состояние хаотизируется настолько, что для его описания достаточно знать, как изменяется во времени распределение по координатам и импульсам всего одной частицы (т. наз. одночастичная ф-ция распределения). На втором этапе релаксации за время порядка времени своб. пробега в результате всего неск. столкновений в макроскопически малых объемах, движущихся со средней скоростью переноса массы (массовая скорость), устанавливается локальное термодинамич. равновесие. Оно характеризуется параметрами состояния (т-рой, хим. потенциалом и др.), к-рые зависят от пространств. координат и времени и медленно стремятся к равновесным значениям в результате большого числа столкновений (процессы теплопроводности, диффузии, вязкости и т.п.). Время релаксации зависит от размера системы и велико в сравнении со средним временем своб. пробега.

В многоатомных газах (с внутр. степенями свободы) м. б. затруднен обмен энергией между поступат. и внутр. степенями свободы (вращат., колебат.) и возникает релаксация, связанная с этим явлением. Быстрее всего устанавливается равновесие по поступат. степеням свободы, к-рое характеризуется соответствующей т-рой. Равновесие между поступат. и вращат. степенями свободы устанавливается значительно медленнее. Возбуждение колебат. степеней свободы возможно лишь при высоких т-рах. Поэтому в многоатомных газах возможны многоступенчатые процессы релаксации (см. Неравновесная химическая кинетика). Если газ состоит из компонентов с сильно различающимися по массам молекулами, замедляется обмен энергий между компонентами, вследствие чего возможны состояния с разл. т-рами компонент. Напр., в плазме различаются ионные и электронные т-ры и происходят медленные процессы их релаксации (см. Плазмохимия).

В жидкостях релаксацию описывают с помощью пространственно-временных корреляц. ф-ций, характеризующих затухание во времени и пространстве взаимного влияния молекул (корреляций). Эти корреляции являются причиной необратимых процессов-теплопроводности и вязкости (см. Жидкость). Время релаксации к полному термодинамич. равновесию можно оценить с помощью кинетич. коэффициентов. Напр., в бинарном р-ре время релаксации концентрации т ! L²/D, где L-размер системы, D-коэф. диффузии; время релаксации т-ры т ! L²/x, где х-коэф. температуропроводности, и т.д. (подробнее см. Макрокинетика).

В твердых телах релаксацию описывают как релаксацию в газе нек-рых квазичастиц. Напр., в кристаллич. решетке при низких т-рах упругие колебания трактуют как газ фононов (акустическая релаксация). В системе спиновых магн. моментов ферромагнетика квазичастицами являются магноны (магнитная релаксация).

При фазовых переходах релаксация может иметь сложный характер. Если переход из неравновесного состояния в равновесное является переходом 1-го рода, система может перейти сначала в метастабильное состояние и затем релаксировать чрезвычайно медленно (см. Стеклообразное состояние). Особенно сложны релаксац. переходы в полимерах, где существует набор (спектр) релаксац. явлений, каждое из к-рых обусловлено своим механизмом. В окрестности точки фазового перехода 2-го рода степень упорядоченности фаз характеризуется параметром порядка, к-рый стремится к нулю, а его время релаксации сильно увеличивается. Еще сложнее характер релаксации из состояний, очень далеких от термодинамич. равновесия. В открытых системах при этом возможны явления самоорганизации.

Измерения времен релаксации используют в хим. кинетике дли изучения процессов, в к-рых быстро устанавливается равновесие (см. Релаксационные методы). Механическая релаксация проявляется в уменьшении во времени напряжения, создавшего в теле деформацию. Механическая релаксация связана с вязкоупру-гостью, она приводит к ползучести, гистерезисным явлениям при деформировании (см. Реология). Применительно к биол. системам термин "релаксация" иногда используют для характеристики времени жизни системы, к-рая к моменту физиологической смерти приходит в состояние частичного равновесия (квазиравновесия) с окружающей средой. В прир. системах времена релаксации разделены, сильными неравенствами; расположение их в порядке возрастания или убывания позволяет рассматривать систему как последовательность иерархич. уровней с разл. степенью упорядоченности структуры (см. Термодинамика иерархических систем).

Лит.: Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Лифшиц Е. М., Питаевский Л. П., Физическая кинетика, в кн.: Теоретическая физика, т. 10, М., 1979; Гладышев Г. П., Термодинамика и макрокинетика природных иерархических процессов, М., 1988; Денисов Е. Т., Кинетика гомогенных химических реакций, 2 изд., М., 1988.