Деформация

ДЕФОРМАЦИЯ механическая (от лат. deformatio-искажение), изменение относит. расстояния между двумя произвольно выбранными точками в теле. В твердых телах деформация приводит к изменению формы или размеров тела целиком или его части, в жидкостях и газах - к течению. Осн. виды деформации - растяжение, сдвиг, кручение, изгиб, сжатие (одноосное или всестороннее). Термин "деформация" относят как к процессу, протекающему во времени, так и к его результату, выражаемому величиной, к-рая характеризует относит. изменение размеров или формы любого мысленно выделенного элемента тела. Различают у п р у г у ю деформацию, полностью исчезающую после удаления вызвавшей ее нагрузки, п л а с т и ч е с к у ю, или деформацию вязкого течения, к-рая остается после снятия вызвавшего ее внеш. воздействия; в я з к о у п р у г у ю, или запаздывающую, к-рая медленно и частично уменьшается после снятия нагрузки под действием протекающих в теле релаксац. процессов. Все реальные твердые тела, в к-рых доминируют упругие деформации, обладают и пластич. св-вами. Однако обычно твердые тела можно считать упругими, пока нагрузка не превысит нек-рого предела; тогда тело либо разрушается, либо становится заметной пластич. деформация. Для жидкостей определяющую роль играют пластич. деформация, хотя всегда можно установить в них существование упругих деформаций. Для газов объемная деформация является упругой, а сдвиговая - необратимой. Деформации измеряют в относит. единицах. Для твердых тел, в к-рых доминируют упругие деформации, в области достаточно малых деформаций (порядка 0,1) выполняется Гука закон. Для эластомеров характерны большие упругие деформации, наз. высокоэластическими (см. Высокоэластическое состояние); они достигают 8-12 единиц; пластич. деформации могут быть неограниченно велики. Теория деформации основана на предположении о сплошности как тела в целом, так и его любых элементарных объемов. Пусть при деформации смещение нек-рой точки А с радиус-вектором r(х, у, z)в точку с радиус-вектором r' (х', у', z') определяется вектором смещения u, так что r' = r + и.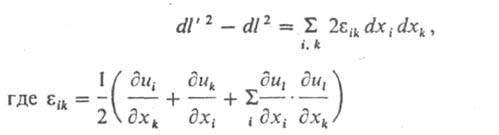

Деформация бесконечно малой окрестности к.-л. точки А определена, если известны изменения бесчисл. множества расстояний от этой точки до всех соседних точек. (Эти изменения расстояний определяют к тому же и изменения при деформации углов между направлениями от точки А к любым двум соседним точкам.) Пусть радиус-вектор к.-л. соседней точки В есть r+dr, к-рый после деформации переходит в радиус-вектор r' + dr', так что dr' = dr+du. Расстояние от исходной точки А до соседней точки В перед деформацией было: dl = (dr, dr)^1/2, после деформации - dl' = (dr', dr')^1/2, так что dl'² = dl² + 2(du, dr) + (du, du); скобки обозначают скалярное произведение векторов. При учете того, что du = S(дu/дx_k)dx_k, (x₁ = х, х₂ = y, х₃ = z) из этого соотношения следует:

Величины e_ii позволяют судить об относит. удлинениях (растяжениях или сжатиях) вдоль направлений по соответствующим координатным осям, a e_ik (i № k) - о сдвигах, т. е. малых деформациях без изменения объема. Для малых деформаций последним членом в скобках можно, как правило, пренебречь. Шесть величин e₁₁, e₂₂, e₃₃, e₁₂ = e₂₁, e₁₃ = e₃₁ и e₂₃ = e₃₂ образуют тензор малой деформации, к-рый полностью определяет деформированное состояние тела. Конечная (большая) деформация тела определяется более сложными выражениями для компонент тензора. Механизм деформации во всех случаях связан с изменением взаимного расположения составляющих тело частиц в-ва. Деформация эластомеров происходит в осн. в результате изменений конформации макромолекул и связана преим. с изменением энтропии системы. Пластич. деформация кристаллич. тел происходит по механизму движения дефектов, гл. обр. скольжения дислокаций, а в случае поликристаллов - путем скольжения по границам зерен. Течение жидкостей обусловлено относит. перемещением молекул. Лит. Ландау Л. Д, Лифшиц Е. М., Теоретическая физика, т. 7 Теория упругости, 4 изд., М., 1987 А. Я Малкин.

Ещё по теме

Структурообразование в дисперсных системах и растворах полимеров

Реология

Твёрдое тело — строение, свойства и классификация

Прочность материалов — термофлуктуационные представления и кинетика разрушения

Реакции в твёрдых телах — механизмы и особенности

Поверхностные явления в физике и химии

Реология — основные понятия и применение

Трение — виды и характеристики

Сжимаемость веществ — основные понятия и применение

Аморфное состояние вещества — свойства и примеры

Механизмы и процессы кристаллизации — от теории к практике