Прочность

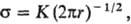
где r-расстояние от конца трещины, К- т. наз. коэф. интенсивности напряжений, к-рый зависит от формы и пластич. св-в материала. При нек-ром критич. значении К_кр трещина распространяется без дополнит. увеличения приложенного напряжения. Разрушающее напряжение s_р для плоского напряженного состояния определяется ф-лой Гриффит-са:

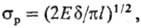
где E-модуль Юнга, d-эффективная поверхностная энергия, l-критич. размер трещины. Для разрушения упруговяз-ких (вязкоупругих) тел, в т. ч. полимерных, прочность определяется условиями образования "шейки" на растягиваемом образце, т.е. условиями нарушения пластич. устойчивости (см. Реология).

Совр. подход к изучению проблем прочности учитывает атом-но-мол. строение твердых тел. Данные об энергии межатомных связей и межмолекулярных взаимод. позволили рассчитать теоретическую прочность твердых тел на разрыв, к-рая оказалась во много раз большей, чем измеряемая на опыте для реальных тел. Расхождение теоретической и практической II. объясняется наличием в телах особых участков - концентраторов напряжений (трещин), в к-рых возникают локальные перенапряжения при приложении к телу нагрузки. Бездефектные материалы обладают прочностью, приближающейся к теоретической; таковы, напр., нитевидные кристаллы.

Кинетика разрушения. Физ. теории рассматривают деформирование и разрушение твердых тел как процессы, при к-рых в исходной структуре развиваются изменения под действием приложенной к телу нагрузки, а также происходят физ.-хим. превращения в поле мех. напряжений, вплоть до катастрофич. разрушения тела, в т.ч. возникновение, перемещение и взаимод. точечных, линейных и объемных дефектов. Эти процессы сильно зависят от т-ры. Описание кинетики процесса требует прямой регистрации возникновения и скорости роста множества трещин или скорости прорастания отдельной магистральной трещины через сечение образца, а на атомномол. уровне-регистрации скорости накопления элементарных актов разрушения, т.е. необратимых разрывов межатомных связей.

Интегральной характеристикой кинетики разрушения служит величина т, наз. долговечностью образца под данной нагрузкой, т.е. промежуток времени от момента приложения нагрузки до разрыва образца, испытываемого на растяжение. Долговечность т-характеристика, обратная средней скорости разрушения. Феноменологич. исследования кинетики разрушения сводятся к изучению зависимости долговечности от т-ры Т и напряжения а, или иначе-температурно-временной зависимости прочности разл. материалов. В определенном диапазоне т-р и растягивающих напряжений для всех материалов справедлива общая закономерность:

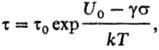
где k-постоянная Больцмана, U₀, g и т₀-эмпирич. коэффициенты. Вид этой ф-лы дает основание считать, что разрушение твердых тел-процесс термофлуктуационный, при к-ром вследствие хаотич. движения составляющих систему частиц энергия теплового движения превышает нек-рый потенц. барьер разрушения U(s), напр. энергию, необходимую для разрыва межатомных связей в твердом теле. Высота барьера линейно уменьшается с увеличением приложенного напряжения. Предэкспоненц. множитель т₀ не зависит от структуры тела и природы межатомных связей и имеет значения порядка 10^-13 с, близкие к периоду собств. колебаний атомов относительно положения равновесия. Это отличает разрушение от др. кинетич. процессов, при к-рых изменения во взаимном расположении частиц (стерич. фактор) меняет Предэкспоненц. множитель на много порядков. Эксперим. значения U₀, близкие к энергии межатомных связей, позволяют считать, что элементарные процессы разрушения представляют собой акты типа разрывов межатомных связей. Величина U₀, как и т₀, не чувствительна к структуре тела. Вся структурная чувствительность прочности сосредоточена в коэф. у. Количественно у, имеющий размерность объема, в десятки и сотни раз больше атомного объема; его значение сильно меняется при легировании и предварит. деформировании металлов, пластифицировании и ориентировании полимеров, др. структурных воздействиях. Величина у имеет смысл произведения нек-рого активац. объема на коэф. перенапряжения в месте развития разрушения.

Термофлуктуац. представления были подтверждены прямым наблюдением за развитием разрушения в аморф-но-кристаллич. ориентированных полимерах на всех уровнях структурной организации. Так, с помощью спектральных методов (ИК, ЭПР, масс-спектрометрия и др.), малоуглового рентгеновского рассеяния и др. было установлено, что в полимерных образцах под нагрузкой распределение напряжений на межатомных связях неоднородно, появляются и накапливаются разорванные связи, концентрируются точечные (молекулярные) дефекты, накапливаются субмикротрещины размером порядка 10³ нм. Сравнение скоростей накопления мол. дефектов и образования субмик-ротрещин привело к выводу о том, что первичные разрывы молекул служат как бы "спусковым крючком" для передачи цепи радикальной р-ции на соседние молекулы, т. е. можно говорить о "взрывном" механизме субмикроразрушения образца. Микрокиносъемка процессов образования и роста микро- и макротрещин подтверждает, что указанные микропроцессы лежат в основе макроскопич. разрушения полимера и определяют его закономерности.

Кинетика разрушения металлич. материалов, стекол и т. п. качественно м. б. рассчитана на основе термофлуктуац. подхода, однако из-за большой чувствительности к структуре тела эмпирич. значения коэф. т₀, U₀ и g в ф-ле для долговечности т могут сильно отличаться от расчетных; в этих случаях интерпретация их физ. смысла затруднительна. Это же относится и к нек-рым полимерам, в частности неориентированным. При анализе кинетики разрушения наряду с термофлуктуац. представлениями учитывают и хим. процессы, сопровождающие деформирование и разрушение (см. Механохимия).

Лит.: Регель В. Р., Слуцкер А. И., Томашевский Э. Е., Кинетическая природа прочности твердых тел, М., 1974; Бартенев Г. М., Прочность и механизм разрушения полимеров, М., 1984; Степанов В. А., Песчан-ская Н. Н., Шпейзман В. В., Прочность и релаксационные явления в твердых телах, Л., 1984; Берштейн В. А., Механогидролитические процессы и прочность твердых тел, Л., 1987; Эмануэль Н. М., Бучаченко А. Л., Химическая физика молекулярного разрушения и стабилизации полимеров, М., 1988. В. Р. Регель.