Диффузия

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я

ДИФФУЗИЯ (от лат. diflusio - распространение, растекание, рассеивание), перенос частиц разной природы, обусловленный хаотич. тепловым движением молекул (атомов) в одно-или многокомпонентных газовых либо конденсир. средах. Такой перенос осуществляется при наличии градиента концентрации частиц или при его отсутствии; в последнем случае процесс наз. самодиффузией (см. ниже). Различают диффузию коллоидных частиц (т. наз. броуновская диффузия), в твердых телах, молекулярную, нейтронов, носителей заряда в полупроводниках и др.; о переносе частиц в движущейся с определенной скоростью среде (конвективная диффузия) см. Массообмен. Переноса процессы, о диффузии частиц в турбулентных потоках см. Турбулентная диффузия. Все указанные виды диффузии описываются одними и теми же феноменологич. соотношениями.
Основные понятия. Главной характеристикой диффузии служит плотность диффузионного потока J - кол-во в-ва, переносимого в единицу времени через единицу площади пов-сти, перпендикулярной направлению переноса. Если в среде, где отсутствуют градиенты т-ры, давления, электрич. потенциала и др., имеется градиент концентрации с (х, t), характеризующий ее изменение на единицу длины в направлении х (одномерный случай) в момент времени t, то в изотропной покоящейся среде

J = -D(дс/дх), (1)

где D - коэффициент диффузии (м²/с); знак "минус" указывает на направление потока от больших концентраций к меньшим. Пространственно-временное распределение концентрации:

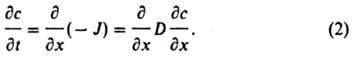
Ур-ния (1) и (2) наз. первым и вторым законами Фика. Трехмерная диффузия [с (х, у, z; t)] описывается ур-ниями:

J = -D grad c (3)

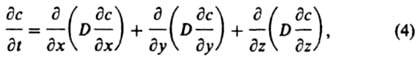
где J - вектор плотности диффузионного потока, grad - градиент поля концентрации. Перенос частиц в среде осуществляется как последовательность их случайных перемещений, причем абс. величина и направление каждого из них не зависят от предыдущих. Диффузионное движение в среде каждой частицы обычно характеризуют среднеквадратичным смещением L² от исходного положения за время t. Для трехмерного пространства справедливо первое соотношение Эйнштейна: L² = GDt. Т. обр., параметр D характеризует эффективность воздействия среды на частицы. В случае диффузии в многокомпонентных смесях в отсутствие градиентов давления и т-ры (изобарно-изотермич. диффузия) для упрощения описания взаимного проникновения компонентов при наличии градиентов их концентраций вводят т. наз. коэффициенты взаимной диффузии. Напр., при одномерной диффузии в двухкомпонентной системе выражение для диффузионного потока одного из компонентов принимает вид:

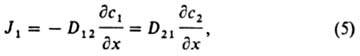
где c₁ + с₂ = const, D₁₂ = D₂₁ - коэф. взаимной диффузии обоих компонентов. В результате неравномерного нагревания среды под влиянием градиента т-ры происходит перенос компонентов газовых или жидких смесей - термодиффузия (в р-рах - эффект Соре).

Если между отдельными частями системы поддерживается постоянная разность т-р, то вследствие термодиффузии в объеме смеси появляются градиенты концентрации компонентов, что инициирует обычную диффузию. Последняя в стационарном состоянии (при отсутствии потока в-ва) уравновешивает термодиффузию, и в системе возникает разность концентраций компонентов. Это влияние лежит в основе одного из методов разделения изотопов, а также термодиффузионного разделения нефтяных фракций. При внеш. воздействии на систему градиента давления или гравитац. поля возникает бародиффузия. Примеры: диффузионное осаждение мелких взвешенных частиц при столкновении их с молекулами газа (см. Пылеулавливание); баромембранные процессы - обратный осмос, микро- и ультрафильтрация (см. Мембранные процессы разделения, Осмос). Действие на систему внеш. электрич. поля вызывает направленный перенос заряженных частиц - электродиффузию. Примеры: электромембранные процессы, напр., электродиализ - разделение под действием электрич. тока ионизированных соед. вследствие избират. переноса ионов через ионообменные мембраны; диффузия носителей заряда - перемещение электронов проводимости и дырок, обусловленное неоднородностями их концентрации в полупроводниках. Математически законы Фика аналогичны ур-ниям теплопроводности Фурье. В основе такой аналогии лежат общие закономерности необратимых процессов перераспределения интенсивных параметров состояния (концентрации, т-ры, давления и др.) между разл. частями к.-л. системы при стремлении ее к термодинамич. равновесию. При малых отклонениях системы от него эти закономерности описываются линейными соотношениями между потоками физ. величин и термодинамич. силами, т. е. градиентами параметров, вызывающими указанные отклонения. В частности, диффузионный поток частиц данного типа, помимо градиентов концентраций частиц каждого типа, может при соответствующих условиях в большей степени определяться градиентами др. интенсивных параметров и внеш. силами. В общем виде связь между потоками и силами описывается феноменологич. ур-ниями термодинамики необратимых процессов. Напр., в случае электронейтральной бинарной газовой системы при наличии градиента т-ры дТ/дх, градиента давления др/дх и градиента электрич. потенциала дj/дx выражение для диффузионного потока частиц с зарядом q_i в одномерном случае принимает вид:

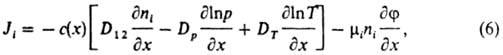
где с - общее число частиц смеси в единице объема; n_i = c_i/c -относит. доля частиц i-гo компонента (i = 1, 2); D_p, D_T - коэф. баро- и термодиффузии; m_i = q_iD/kТ (соотношение Нернста - Эйнштейна) - подвижность частиц 1-го компонента в электрич. поле; k - постоянная Больцмана; T - абс. т-ра. Напр., в бинарной газовой смеси при постоянном давлении и отсутствии внеш. сил полный диффузионный поток

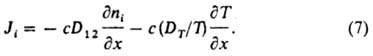
При отсутствии потока (J = 0) распределение концентраций находят по ф-ле:

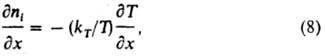
где k_T = D_T/D₁₂. Коэф. D_T в значит. степени зависит от межмолекулярного взаимод., поэтому его изучение позволяет исследовать межмолекулярные силы в разл. средах. Одновременно с диффузионным переносом частиц посторонних в-в (примесей), неравномерно распределенных в к.-л. среде, происходит самодиффузия - случайное перемещение частиц самой среды, хим. состав к-рой при этом не изменяется. Данный процесс, наблюдаемый даже в отсутствие в системе термодинамич. сил, описывается ур-ниями Фика, в к-рых D заменен параметром D_c, называемым коэф. самодиффузии. Эффекты самодиффузии могут приводить к сращиванию двух пришлифованных образцов одного и того же в-ва, спеканию порошков при пропускании через них электрич. тока, к растягиванию тел под действием подвешенного к ним груза (диффузионная ползучесть материалов) и т. д. При взаимной диффузии в твердых телах поток атомов одного сорта может превосходить идущий в обратном направлении поток атомов др. сорта, если для нескомпенсир. вакансий (а возможно, и для нескомпенсир. атомов) имеются стоки. При этом в кристалле появляются поры, приводящие к нарушению устойчивости кристаллич. решетки как мех. системы и, вследствие этого, к смещению кристаллич. плоскостей как целого (эффект Киркиндаля). В частности, при взаимной диффузии в бинарных металлич. системах наблюдается перемещение "инертных" меток, напр., тонких тугоплавких проволочек из Мо или W диаметром неск. мкм, внесенных в зону диффузии. Скорость диффузионного массопереноса в разл. в-вах или материалах иногда удобно характеризовать константой их проницаемости П = Dg, где g - константа Генри, определяющая равновесную р-римость переносимого компонента. В частности, выражение для стационарного потока молекул газа, диффундирующих через разделит. перегородку (мембрану) толщиной d, имеет вид: J = ПgDр/d, где Dр - разность парциальных давлений разделяемых компонентов газовой смеси по обе стороны перегородки. Коэф. диффузии существенно различаются для диффузионных процессов в газовых и конденсированных (жидких и твердых) средах: наиб. быстро перенос частиц происходит в газах (D порядка 10^-4 м²/с при нормальных т-ре и давлении), медленнее - в жидкостях (порядка 10^-9), еще медленнее - в твердых телах (порядка 10^-12). Проиллюстрируем указанные выводы на примерах молекулярной диффузии.
Диффузия в газовых средах. Для оценки D в качестве характерного (среднего) смещения частиц принимают длину своб. пробега молекул l = ut, где и и t - средние скорость движения частиц и время между их столкновениями. В соответствии с первым соотношением Эйнштейна D ~ l²t^-1; более точно D = 1/3 lu. Коэф. диффузии обратно пропорционален давлению р газа, поскольку l ~ 1/р; с повышением т-ры Т (при постоянном объеме) D возрастает пропорционально T^1/2, т. к. 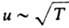; с увеличением мол. массы газа D снижается. Согласно кинетич. теории газов, коэф. взаимной диффузии газов А и В в бинарной смеси (табл. 1)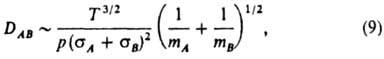

где р - полное давление в системе, т_A и т_B - массы газов, s_A и s_B - параметры потенциала Леннард-Джонса (см., напр., Абсорбция).

Большой практич. интерес представляет перенос газов через сквозные поры в твердых телах. При относительно малых давлениях газа или размерах пор (r₀), когда частота столкновений молекул газа со стенками пор превышает частоту взаимных столкновений молекул, т. е. средняя длина их своб. пробега l >> r₀ (для нормального давления при r₀ < 10^-7 м), наблюдается т. наз. кнудсеновская диффузия. При этом газовый поток через пористую перегородку пропорционален средней скорости молекул и константа газопроницаемости определяется из ур-ния:

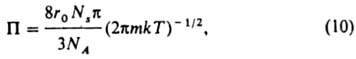
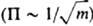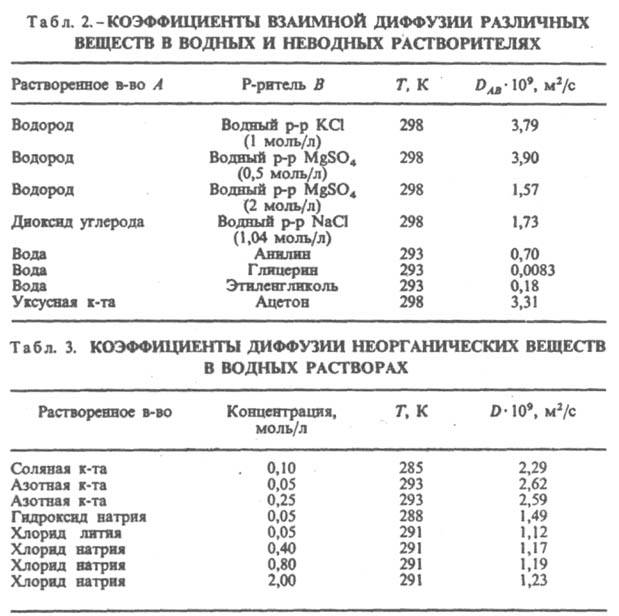
где N_s - поверхностная плотность пор в перегородке. Поскольку средняя скорость молекул обратно пропорциональна квадратному корню из их масс , компоненты разделяемой газовой смеси проникают через поры мембраны с разл. скоростями; в результате прошедшая через перегородку смесь обогащается более легкими компонентами. С увеличением давления газа в таких пористых системах возрастает поверхностная концентрация молекул, адсорбированных на стенках пор. Образовавшийся адсорбц. слой может оказаться подвижным и перемещаться вдоль пов-сти поры, вследствие чего параллельно с объемным диффузионным переносом в ней возможна поверхностная диффузия газа. Последняя оказывает иногда существ. влияние на кинетику хим. превращений, обусловливая неравновесное распределение в системе взаимод. реагентов.
Диффузия в конденсированных средах. В жидкостях и твердых телах диффузия осуществляется перескоками частиц из одного устойчивого положения в другое, расстояние между ними имеет порядок межмолекулярного. Для таких перескоков необходимы локальная перестройка ближнего окружения каждой частицы (вероятность перестройки характеризуется энтропией активации DS) и случайное накопление в этой области нек-рого кол-ва тепловой энергии E_D (энергия активации диффузии). После перескока каждая частица оказывается в новом энергетически выгодном положении, а выделяющаяся энергия рассеивается в среде. При этом D = D₀exp(-E_D/RT), где D₀ = nexp (DS/R) - энтропийный фактор, зависящий от частоты "тепловых ударов" молекул среды (n ~ 10¹² с^-1), R - газовая постоянная. Диффузионное движение частиц в жидкости определяется ее вязкостными св-вами, размерами частиц и характеризуется их т. наз. подвижностью ( ~ D/kT откуда D ~ (kT (второе соотношение Эйнштейна). Параметр ( - коэф. пропорциональности между скоростью частицы и и движущей силой F при стационарном движении с трением (и = (F). Напр., в случае сферически симметричных частиц радиусом г. для к-рых ( = 1/6prh(T), справедливо ур-ние Стокса-Эйнштейна: D = kT/6prh(T), где h(T) - коэф. динамич. вязкости среды в функции от т-ры. Повышение D с увеличением т-ры в жидкостях объясняется уменьшением плотности упаковки их молекул ("разрыхлением структуры") при нагр. и, как следствие, возрастанием числа перескоков частиц в единицу времени. Коэф. диффузии разных в-в в жидкостях приведены в табл. 2 и 3; характерные значения E_D ~ 20-40 кДж/моль.


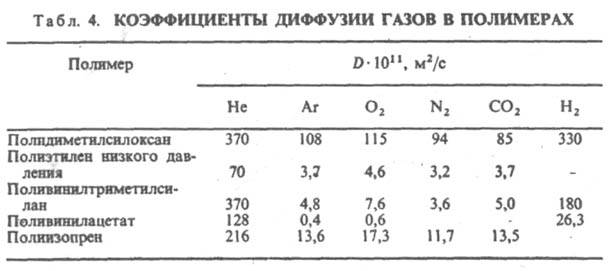
Коэф. диффузии в твердых орг. телах имеют значит. разброс, достигая в ряде случаев значений, сравнимых с соответствующими параметрами в жидкостях. Наиб. интерес представляет диффузия газов в полимерах. Коэф. диффузии в них (табл. 4) зависят от размеров диффундирующих молекул, особенностей взаимод. их с фрагментами макромолекул, подвижности полимерных цепей, своб. объема полимера (разность между реальным объемом и суммарным объемом плотно упакованных молекул) и неоднородностью его структуры.

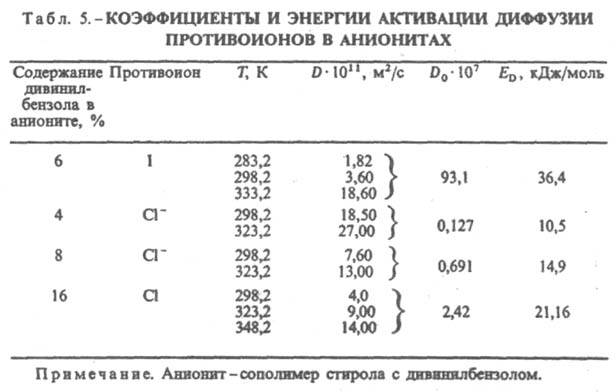
Высокие значения D при т-рах выше т-ры стеклования полимеров обусловлены большой подвижностью в данных условиях фрагментов макромолекул, что приводит к перераспределению своб. объема и соотв. к возрастанию DS и уменьшению E_D. При т-рах ниже т-ры стеклования коэф. диффузии имеют, как правило, меньшие значения. При диффузии в полимерах жидкостей значения D могут зависеть от концентрации растворенных компонентов вследствие их пластифицирующего действия. Коэф. диффузии ионов в ионообменных смолах в значит. степени определяются их влагосодержанием (среднее число п молекул воды, приходящееся на одну ионогенную группу). При высоком влагосодержании (п > 15) коэф. диффузии сопоставимы с соответствующими D для ионов в электролитах (см. табл. 5 и 3). При п < 10 коэф. диффузии экспоненциально снижаются с уменьшением п.

В твердых неорг. телах, где доля своб. объема и амплитуды колебаний атомов кристаллич. решетки незначительны, диффузия обусловлена наличием нарушений в их структуре (см. Дефекты в кристаллах), возникающих при изготовлении, нагревании, деформациях и др. воздействиях. При этом м. б. реализованы неск. механизмов диффузии: обмен местами атомов и обмен местами двух соседних атомов, одновременное циклич. перемещение неск. атомов, передвижение их по междоузлиям и др. Первый механизм преобладает, напр., при образовании твердых р-ров замещения, последний - твердых р-ров внедрения. Диффузионные процессы происходят с заметной скоростью только при высоких т-рах. Напр., как следует из табл. 6, коэф. диффузии О₂ в СаО и Сr₂О₃ при повышении т-ры с 20 до 300 °С возрастают соотв. в 2.10¹⁰ и 3.10³⁹ раз. При массoпереносе в области линейных дислокаций и по поверхностным (границы зерен) дефектам в поликристаллич. телах D увеличиваются на 4-5 порядков.

Для определения коэф. диффузии расчетные данные (концентрац. профили и потоки диффундирующих частиц, сорбиционно-десорбц. закономерности) сравнивают с экспериментальными. Последние находят с помощью разл. физ.-хим. методов: изотопных индикаторов, рентгеновского микроанализа, гравиметрии, масс-спектрометрии, оптических (рефрактометрия, ИК спектроскопия) и др.
Значение диффузионных процессов. Диффузия играет важную роль в разл. областях науки и техники, в процессах, происходящих в живой и неживой природе. Диффузия оказывает влияние на протекание или определяет механизм и кинетику хим. р-ций (см., напр., Диффузионных пламен метод, Макрокинетика), а также мн. физ.-хим. процессов и явлений: мембранных, испарения, конденсации, кристаллизации, растворения, набухания, горения, каталитических, хроматографических, люминесцентных, электрич. и оптич. в полупроводниках, замедления нейтронов в ядерных реакторах и т. д. Большое значение имеет диффузия при образовании на границах фаз двойного электрич. слоя, диффузиофорезе (см. Электроповерхностные явления) и элекрофорезе (см. Электрокинетические явления), в электрохим. методах анализа и процессах (см., напр., Диффузионный потенциал, Диффузионный ток), в фотографич. процессах для быстрого получения позитивного изображения и др. Диффузия служит основой мн. распространенных техн. операций: спекания порошков, химико-термич. обработки металлов (напр., азотирования и цементации сталей), гомогенизации сплавов, металлизации и сварки материалов, дубления кожи и меха, крашения волокон; перемещения газов с помощью т. наз. диффузионных насосов. Диффузия - одна из стадий многочисл. химико-технол. процессов (напр., массообменных); представления о диффузионном переносе в-ва используют при моделировании структуры потоков в хим. реакторах и др. Роль диффузии существенно возросла в связи с необходимостью создания материалов с заранее заданными св-вами для развивающихся областей техники (ядерной энергетики, космонавтики, радиационных и плазмохим. процессов и т. п.). Знание законов, управляющих диффузией, позволяет предупреждать нежелательные изменения в изделиях, происходящие под влиянием высоких нагрузок и т-р, облучения и т. д. Закономерностям диффузии подчиняются процессы физ.-хим. эмиграции элементов в земных недрах и во Вселенной, а также процессы жизнедеятельности клеток и тканей растений (напр., поглощение корневыми клетками N, Р, К - осн. элементов минер. питания) и живых организмов.
===
Исп. литература для статьи «ДИФФУЗИЯ»: Франк-Каменецкий Д. А., Диффузия и теплопередача в химической кинетике, 2 изд., М., 1967; Хаазе Р., Термодинамика необратимых процессов, пер. с нем., М., 1967; Процессы взаимной диффузии в сплавах, под ред. К. П. Гурова, М., 1973; Берд Р., Стьюарт В., Лайтфут Е., Явления переноса, пер. с англ., М., 1974; Кофстад П., Отклонение от стехиометрии, диффузия и электропроводность в простых окислах металлов, пер. с англ., М., 1975; Николаев Н. И., Диффузия в мембранах, М., 1980; Шервуд Т., Пигфорд Р., Уилки Ч., Массопередача, пер. с англ., М., 1982; Физический энциклопедический словарь, М., 1983, с. 174-75, 652, 754; Овчинников А. А., Тимашев С. Ф., Белый А. А., Кинетика диффузионно-контролируемых химических процессов, М., 1986; Чалых А. Е., Диффузия в полимерных системах, М., 1987. С. Ф. Тимашев.

Страница «ДИФФУЗИЯ» подготовлена по материалам химической энциклопедии.

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я