1.4. Образование коллоидных систем при диспергировании
Получение коллоидных систем при диспергировании не связано с изменением агрегатного состояния, поэтому энергия Гиббса образования частиц связана исключительно лишь с той работой по преодолению сил межмолекулярного притяжения, которую необходимо совершить для образования новой поверхности. Эта работа описывается уравнением (2.1.11):
.
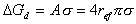В связи c тем, что при диспергировании форма частиц может быть произвольной, в этом уравнении вводится некоторый эффективный радиус ref, который имела бы сферическая частица одинакового с реальной частицей объема.
Возможен также другой вид уравнения для энергии Гиббса образования частиц, если форму частиц можно определить, а характерный линейный размер (диаметр, длина ребра куба, длина цилиндра и т.д.) может быть измерен:
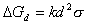, (2.1.42)
где k – коэффициент формы частиц.
Уравнения (2.1.11) и (2.1.42) справедливы в том случае, если можно пренебречь работой, направленной на преодоление упругой и пластической деформации тела при диспергировании. Это возможно на второй стадии, когда размер частиц невелик. На первой стадии диспергирования следует учитывать работу деформирования:
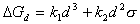, (2.1.43)
где k1– коэффициент, равный работе деформирования единицы объема.
Диспергирование обычно используют для измельчения пигментов, применяемых для нанесения печатных рисунков на текстильные материалы.
При диспергировании свободная энергия системы растет, получаемые дисперсные системы оказываются неустойчивыми, если не использовать специальные стабилизаторы, снижающие избыточную удельную свободную энергию. Принципы стабилизации мы рассмотрим далее.