Электрическая составляющая расклинивающего давления. Энергия отталкивания
Природа сил отталкивания, проявляющихся при сближении частиц и перекрытии двойных электрических слов (ДЭС) сложнее, чем кулоновское электростатическое взаимодействие. Хотя мы и будем употреблять термин «электрическая» составляющая расклинивающего давления, понимать следует тот вклад ионов диффузной обкладки ДЭС двух частиц, в результате которого происходит нарушение термодинамического равновесия и возникает осмотический поток растворителя в зазор между частицами, препятствующий их дальнейшему сближению.
Рассмотрим случай сближения двух частиц в растворе электролита с концентрацией C0 (кмоль/м3), причем будем полагать, что радиус кривизны поверхности частиц несоизмерим с толщиной диффузной обкладки ДЭС, т.е. r >> k-1, где k - параметр Дебая. При перекрытии диффузных обкладок потенциал в объеме двойного слоя ни одной из частиц не достигает нулевого значения. Схема изменения потенциала при перекрытии ДЭС двух частиц приведена на рис. 2.21. Минимальное значение потенциала jmin= jh будет на расстоянии h, т.е. ровно посередине зазора между частицами. Обозначим потенциал на поверхности твердого тела j0. Потенциал в остальных точках ДЭС будет зависеть только от расстояния до твердой поверхности jx =f(x). Очевидно, что при x=hdj /dx =0.
Потенциал в зазоре на расстоянии х до поверхности частицы будет усредненным по плоскости, параллельной поверхности и плотность заряда будет иметь величину rx.
|
При выводе уравнения для энергии отталкивания теории Дерягина-Ландау-Фервея-Овербека (ДЛФО) в качестве рабочей модели ДЭС примем модель и теорию Гуи-Чепмена. Наличие в зазоре между частицами повышенной по сравнению с раствором концентрации ионов Ch > C0 приведет к разности осмотических давлений в зазоре между частицами (Рh) и в растворе (Р0):
P = Ph - P0 . (2.3.28)
Чем больше концентрация ионов в зазоре Ch , тем выше Рh и, следовательно, должен быть интенсивнее поток жидкости, устремляющийся из раствора в зазор и стремящийся выровнять осмотическое давление. Наряду с этим действуют силы электростатического взаимодействия, определяемые потенциалом поверхности j0 и плотностью заряда. Задача состоит в том, чтобы выразить избыточное осмотическое давление в зазоре через экспериментально определяемую характеристику ДЭС. Такой характеристикой является поверхностный потенциал.
Если сближение частиц происходит квазиравновесно, как предположили Фервей и Овербек, то изменения осмотического давления уравновешиваются изменением потенциала, т.е.
dP + r dj = 0, (2.3.29)
откуда
dP = - r dj. (2.3.30)
Интегрирование этого уравнения проводят в пределах от 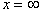 до x = h и, соответственно, от P0 до Ph и от j = 0 доj h :
до x = h и, соответственно, от P0 до Ph и от j = 0 доj h :
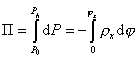 . (2.3.31)
. (2.3.31)
Из теории строения ДЭС Гуи-Чепмена следует, что
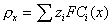 , (2.3.32)
, (2.3.32)
где zi – заряд ионов i-того сорта, F – число Фарадея, Ci(x) – концентрация ионов в точке х диффузионной обкладки двойного электрического слоя.
Для симметричного бинарного электролита, т.е. при z+ = z- = =z, предполагая, что распределение концентрации ионов в ДЭС подчиняется закону распределения Больцмана, из уравнения (2.3.32) получаем
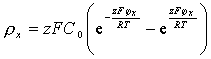 , (2.3.33)
, (2.3.33)
где С0 – концентрация электролита в растворе (межмицеллярной жидкости).
При малых потенциалах поверхности частиц, т.е. если zFjx << RT, что реализуется приj0 < 50 мВ, разложение в ряд экспоненциальной функции в скобках уравнения (2.3.33) можно ограничить первым членом, тогда
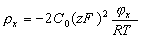 . (2.3.34)
. (2.3.34)
Подставляя уравнение (2.3.34) в уравнение (2.3.31), получаем
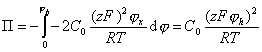 ,
,  (2.3.35)
(2.3.35)
но из теории Гуи–Чепмена
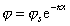 , (2.3.36)
, (2.3.36)
где js– потенциал в плоскости Штерна, поэтому из уравнения (2.3.35) получаем
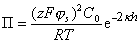 , (2.3.37)
, (2.3.37)
где k – параметр Дебая.
Для симметричного электролита, т.е. такого электролита, у которого анион и катион имеют одинаковую величину заряда,
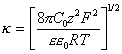 , (2.3.38)
, (2.3.38)
где e0 - диэлектрическая постоянная (e0=8,85×10-12 Ф/м).
Энергию отталкивания (электрическую составляющую расклинивающего давления) можно определить решив уравнение
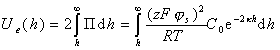 . (2.3.39)
. (2.3.39)
Этот интеграл представляет собой ту работу, которую необходимо будет затратить для сближения двух частиц с бесконечно большого расстояния до расстояния h (в расчете на единицу площади поверхности частиц).
Обозначая (zFjs)/(RT) = u0 (безразмерный потенциал) и интегрируя уравнение (2.3.39) для энергии отталкивания, получаем
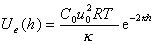 . (2.3.40)
. (2.3.40)
Это уравнение показывает, что уменьшение расстояния между частицами после перекрытия диффузионных оболочек ДЭС экспоненциально увеличивает энергию отталкивания.
Отметим еще раз, что уравнение (2.3.40) справедливо лишь для плоских частиц, имеющих малый потенциал поверхности (j0<50мВ) в растворе симметричных электролитов (z+= z-). Для случаев высокого потенциала поверхности частиц сферической формы при соизмеримых радиусе кривизны и толщине диффузной обкладки ДИС (r »k-1) уравнения получаются значительно сложнее.
Для плоских частиц при любых, но одинаковых, значениях потенциалов поверхности Дерягин получил уравнение
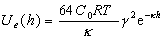 ,
, (2.3.41)
(2.3.41)
где
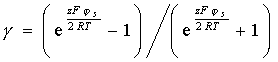 . (2.3.42)
. (2.3.42)
Уравнение (2.3.41) при малых значениях потенциалов поверхностей частиц переходит в удобную для расчетов форму
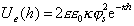 . (2.3.43)
. (2.3.43)
В этих уравнениях Ue(h) – энергия отталкивания частиц на расстоянии h; ee0 – диэлектрическая проницаемость среды; z – заряд ионов в растворе с концентрацией С0; F – число Фарадея; Т – температура, К; k – параметр Дебая; h – наименьшее расстояние между частицами; js– потенциал поверхности в плоскости Штерна.
Для малых значений потенциала поверхности (js) энергия отталкивания сильно зависит от его величины и пропорциональна квадрату потенциала. При высоких значениях js его влияние не столь резко, хотя в неявном виде оно проявится через постояннуюg. Это связано с тем, что увеличение потенциала поверхности приводит к усилению притяжения противоионов к поверхности и их подвижность, а следовательно, и избыточное осмотическое давление будут снижаться.
Для одинаковых сферических частиц с любым потенциалом поверхности в растворах симметричных электролитов Дерягин предложил уравнение
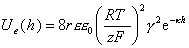 . (2.3.44)
. (2.3.44)
При условии, что h » r >> 1/k уравнение (2.3.44) переходит в
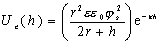 . (2.3.45)
. (2.3.45)
Для приближенных расчетов электрической составляющей энергии расклинивающего давления Маккартни и Левин получили уравнение для одинаковых сферических частиц с малыми потенциалами
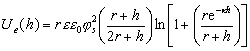 , (2.3.46)
, (2.3.46)
которое при h << r переходит в
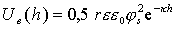 . (2.3.47)
. (2.3.47)
К такой же форме приводится и уравнение Дерягина (2.3.44) при малом перекрытии диффузионных слоев (kh = 2¸3) и малом потенциале поверхности.
Труднее рассчитать энергию парного отталкивания частиц, имеющих на своей поверхности различные потенциалы. Так для сферических частиц, имеющих произвольные потенциалы j1 иj2, Фюрстенау предложил следующее уравнение для расчета энергии электрической составляющей расклинивающего давления в растворе симметричного электролита при r1 и r2 , существенно большими толщины диффузионной части двойного ионного слоя:
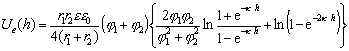 ,(2.3.49)
,(2.3.49)
где r1, r2 – радиусы взаимодействующих частиц сорта 1 и 2; j1 , j2 – их потенциалы.
Для расчета энергии отталкивания на больших расстояниях уравнение можно упростить. При условии 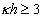 уравнение (2.3.49) принимает вид
уравнение (2.3.49) принимает вид
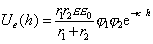 . (2.3.50)
. (2.3.50)
Расчет электрической компоненты энергии отталкивания двух различных по природе частиц с различными потенциалами в растворах симметричных электролитов можно проводить по наиболее строгому уравнению Дерягина:
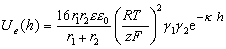 , (2.3.51)
, (2.3.51)
где g1 и g2 рассчитывают по уравнению (2.3.42).
Для расчета электрической компоненты энергии отталкивания сферической частицы с плоскостью (например, взаимодействия частиц полимера латекса с волокном) Ямамура получил уравнение
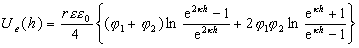 , (2.3.52)
, (2.3.52)
где j1,j2- потенциал частиц и плоской поверхности.
Энергия отталкивания сферических частиц, как видно из приведенных уравнений, пропорциональна их радиусу. Если радиус мал, то энергия отталкивания оказывается величиной одного порядка с энергией теплового движения. Поэтому тонкодисперсные системы обычно менее агрегативно устойчивы. Энергия притяжения таких частиц в соответствии с уравнения (2.3.24) снижается также пропорционально уменьшению размера частиц.
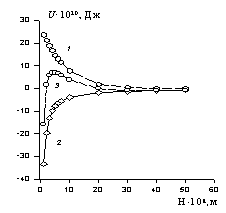
Рис. 2.22. Зависимость потенциальной энергии взаимодействия сферических частиц полимера в латексе от расстояния между ними. Энергия взаимодействия: 1- отталкивания, 2- притяжения, 3- суммарная |
Приведенные выше уравнения для расчета энергии отталкивания при парном взаимодействии частиц не учитывают собственный объем ионов, их сольватацию, специфический адсорбционный потенциал, который проявляется при коагуляции дисперсий электролитами, когда коагулирующая способность ионов одинаковой валентности четко соответствует рядам Гофмейстера. Теоретический учет всех этих поправок невозможен.
Суммарная энергия взаимодействия частиц выражается в виде кривой потенциальной энергии. Так, для плоских частиц и сферических частиц при r >> k-1, в частности для слабо заряженных одинаковых поверхностей, в расчете на единицу площади поверхности, учитывая уравнения (2.3.22) и (2.3.40), получаем
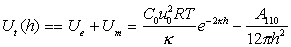 . (2.3.53)
. (2.3.53)
Для других систем поступают аналогично. Расчет потенциальной энергии взаимодействия частиц в устойчивых системах приводит к зависимости, пример которой показан на рис. 2.22.
Расчет был сделан для латекса синтетического полимера, у которого размер частиц составляет 100×10-9 м, электрокинетический потенциал равен 25×10-3 В, постоянная Гамакера А* = 2,5×10-21 Дж.
Кривые, лежащие в области отрицательной энергии, соответствуют энергии притяжения, а лежащие в положительной области – отталкивания. Потенциальный барьер, равный примерно 10 kT, свидетельствует об устойчивости данной системы.

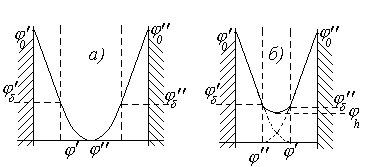 Рис. 2.21. Схема изменения потенциала в зазоре между частицами: a– до перекрытия, б – после перекрытия
Рис. 2.21. Схема изменения потенциала в зазоре между частицами: a– до перекрытия, б – после перекрытия