Коагуляция дисперсных систем, стабилизированных неионогенными ПАВ
Можно найти ряд сходных моментов в нарушении устойчивости дисперсных систем, стабилизированных неионогенными ПАВ, с коагуляцией стерически стабилизированных дисперсий. В частности повышение температуры выше температуры помутнения водных растворов неионогенных ПАВ способно вызвать необратимый процесс коагуляции, например латекса, стабилизированного таким ПАВ. Этот процесс температурной коагуляции, связанный с дегидратацией оксиэтиленовых цепочек неионогенных ПАВ, подобен температурной коагуляции стерически стабилизированных систем.
Коагуляция под действием электролитов возможна не только в результате дегидратации, но и при изменении осмотического равновесия между дисперсионной средой и адсорбционно-сольватными оболочками частиц дисперсной фазы.
При теоретическом рассмотрении процесса коагуляции дисперсных систем, стабилизированных неионогенными ПАВ, можно использовать тот же принцип нарушения устойчивости, который мы использовали при обсуждении электролитной коагуляции, - равенство при коагуляции потенциальных энергий притяжения и отталкивания.
Очевидно, что условия Ut = 0 при Us =Um и dUt/dh = 0 будут соответствовать пороговым (критическим) значениям температуры и (или) концентрации коагулирующего вещества. При таких значениях температуры или концентраций ( или одновременного действия обоих параметров) будет происходить быстрая коагуляция систем с адсорбционно-сольватным фактором стабилизации.
В связи с тем, что количественной теории гидратации не существует и нельзя теоретически предсказать (а тем более количественно оценить) гидратацию при различных заданных значениях температуры и концентрации коагуляторов, приходится проводить экспериментальное исследование и выявлять зависимость чисел гидратации и толщины адсорбционно-сольватных оболочек частиц от природы стабилизатора, температуры, концентрации различных веществ электролитной и неэлектролитной природы.
Дисперсные системы с химически локализованным стабилизатором обычно более устойчивы, чем системы с адсорбционно-сольватными слоями. Коагуляция таких систем происходит при более высокой температуре и существенно более высоких концентрациях электролита. Эффективность локализованного стабилизатора оказывается выше, чем у адсорбированного неионогенного ПАВ с эквивалентным количеством оксиэтиленовых групп.
Связано это с тем, что локализованный стабилизатор не может смещаться по поверхности частиц и удаляться при их слипании, поэтому устойчивость таких систем определяется прочностью сольватных оболочек, а коагуляция может произойти при ослаблении и частичной или полной деструкции сольватного слоя под действием внешних факторов – нагревания, добавок электролитов и неэлектролитов.
Расчет энергии отталкивания сферических частиц по уравнению (2.3.118) для латексов, стабилизированных адсорбционно-сольватными слоями неионогенных ПАВ, и полной энергии взаимодействия полимерных частиц в латексах с учетом энергии притяжения приводит к зависимостям, пример которых показан на рис. 2.24. Из приведенных данных видно, что потенциальная энергия отталкивания адсорбционно-сольватных слоев частиц при 25oC на 2-3 порядка превышает потенциальную энергию притяжения. Даже при степени гидрофилизации поверхности a = 0,6 такие системы оказываются устойчивыми. Однако на расстояниях, больших двойной толщины гидратных оболочек, где проявляется лишь энергия притяжения частиц, возможна их фиксация во втором потенциальном минимуме, глубина которого составляет 2-4 kT.
|
Повышение температуры или введение сравнительно небольших количеств электролита несколько снижает потенциальную энергию отталкивания гидратных оболочек, однако она еще превышает энергию притяжения на 1-2 порядка. Поэтому нарушение устойчивости таких дисперсных систем происходит лишь при одновременном действии нагревания и введения достаточно больших количеств электролитов.
Критерий коагуляции дисперсных систем, стабилизированных неионогенными ПАВ получают из предпосылки, что энергия отталкивания Us = 0. Тогда из уравнения (2.3.118) следует
Сс = 3,5×103 iWе/(WhMе), (2.3.136)
где Сс – критическая концентрация коагуляции (для электролитов выражается в г-экв/л).
Экспериментальная проверка показала, что уравнение (2.3.136) может с достаточной степенью достоверности предсказать критическую концентрацию коагулятора дисперсий (латексов), стабилизированных неионогенными ПАВ и даже стабилизированных гибкими линейными полимерными молекулами. В последнем случае при расчетах по уравнению (2.3.136) берут молекулярную массу не всей макромолекулы, а её статистического сегмента.

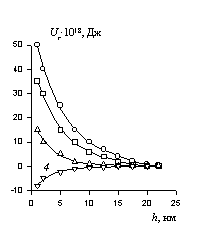 Рис. 2.24. Потенциальные кривые энергии взаимодействия частиц в дисперсии ПВА, стабилизированной неионогенным ПАВ-ОП-10. Концентрация электролита NH4H2PO4: 1-0; 2-0,05; 3-0,15; 4-0,2 кмоль/м3
Рис. 2.24. Потенциальные кривые энергии взаимодействия частиц в дисперсии ПВА, стабилизированной неионогенным ПАВ-ОП-10. Концентрация электролита NH4H2PO4: 1-0; 2-0,05; 3-0,15; 4-0,2 кмоль/м3
