7.2.8. Определение размера капель и характеристика распределения их по размерам. Микроскопия

Микроскопическое определение гранулометрического состава капель эмульсии представляет собой один из наиболее традиционных методов анализа. Метод с использованием оптического микроскопа ограничен размером частиц 5·10^-7м в связи с тем, что меньшие частицы уже не отражают свет. Электронный микроскоп применяют для частиц размером 10^-9-10^-5 м. Размер более крупных капель измеряют с помощью оптического микроскопа. Обычно для проведения микроанализа берут пробу разбавленной исследуемой эмульсии с добавками ПАВ. Пробу-порошок помещают на предметное стекло и измеряют размеры капель с помощью окулярной сетки или шкалы. Обычно измеряют все капли, находящиеся в поле зрения. Число измеренных капель определяется заданной точностью анализа. Очевидно, что чем больше охарактеризовано капель, тем точнее результат.

Точность микроскопического анализа зависит от двух факторов: один из них - субъективные ошибки, другой обусловлен статистическим характером измерений. Достаточная точность измерений достигается при подсчете размера около 1000 капель каждой фракции. Поэтому точность определения размера крупных капель, которых обычно мало в поле микроскопа, как правило, невелика. В то же время, если капли имеют размер на границе разрешающей способности микроскопа или даже за нею, то определить их размер, а тем более содержание, практически невозможно. В этой связи для анализа эмульсий с каплями таких размеров применяют электронный микроскоп.

Обычно размер капель характеризуют их диаметром. Для капель разбавленной эмульсии, которые имеют правильную сферическую форму, диаметр точно характеризует все остальные параметры: объем, поверхность, удельную поверхность. В связи с тем, что капли в эмульсиях имеют, как правило, достаточно широкое распределение по размерам, говорят о некотором среднем диаметре.

Точность измерения повышается при использовании проецирующих микроскопов или приборов с телевизионной приставкой. Высокая точность подсчета характерна для микроскопов с автоматическим измерением числа частиц и их размера. Такие приборы в настоящее время не являются дефицитными.

Результаты измерения числа капель и их размера выражают в виде некоторой средней величины, в качестве которой наиболее часто используют

-средний арифметический диаметр ,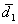

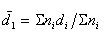, (2.7.6)

где d_i– средний диаметр капель в интервале числа капель n_i ; Sn – общее число подсчитанных капель;

-средний квадратичный (средний по поверхности) размер капель ,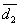

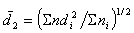, (2.7.7)

- средний кубичный (средний по объему или массе) размер капель ,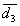

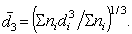
(2.7.8)

Для наиболее полной характеристики эмульсий используют распределение капель по размерам в дифференциальной или интегральной форме. Для этого переходят от числа капель к их массе. Для массы всех капель фракции d_i (от d₁ до d₂, где d₁- наименьший диаметр внутри фракции, d₂- наибольший), можем записать

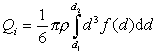, (2.7.9)

где r – плотность вещества капель; f(d) = dN / dx – функция распределения числа капель по размерам.

Полагая, что в узком интервале размеров капель распределение равномерное, т.е.

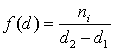, (2.7.10)

где n – число частиц в интервале размеров d₁< d_i < d₂, можем рассчитать массу всех капель в этом узком интервале:

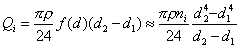. (2.7.11)

Общая масса всех капель в исследуемой эмульсии в интервале размеров от d_minдо d_maxсоставит

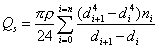. (2.7.12)

После расчета масс каждой фракции результаты выражают в виде таблиц или графиков

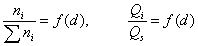. (2.7.13)

С целью повышения вязкости дисперсионной среды, что необходимо для предотвращения броуновского движения мелких капель в момент микроскопирования и исключения коалесценции капель эмульсии используют раствор полимера. Обычно из образцов эмульсии отбирают 1-2 капли, тщательно смешивают на часовом стекле с 5-8 каплями подогретого раствора полимера, затем 1 каплю переносят на предметное стекло и осторожно накрывают покровным стеклом. Препарат готов для микроскопирования.

При микроскопировании в одном поле зрения не должно находиться более 30 капель. Подсчет ведут в 8-10 полях зрения.

При подсчете числа и измерении размера капель нужно следить за тем, чтобы они полностью находились в поле зрения. Капли, находящиеся за пределами сетки, не считают.

Средний радиус капель в каждой фракции рассчитывают по формуле

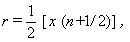(2.7.14)

где x – цена деления шкалы при выбранном увеличении; n – число делений шкалы, в котором укладывается капля.

Расчет численного содержания частиц каждой фракции проводят по формуле

N_i= (100 n_i/Sn_i)% . (2.7.15)

Массовое содержание капель каждой фракции Q_i(%) определяют по формуле (2.7.11), а общую массу капель Q_sнаходят по формуле (2.7.12).

Построение интегральной кривой проводят откладывая на графике значения Q_iдля всех фракций, начиная с наименьшего размера капель, а на оси абсцисс - их размер r_i, рис. 2.66, а. Дифференциальную кривую строят после аналитического или графического дифференцирования интегральной кривой распределения. На рис. 2.66,б показан пример графического дифференцирования. Для такой обработки интегральной кривой распределения можно выбрать произвольный интервал изменения размера капель, но так, чтобы было выделено не менее 10 отрезков на оси абсцисс. Затем проводят линии, параллельные осям ординат, и находят численные значения отрезков Dr_i и DN_i с учетом выбранного масштабного коэффициента, рассчитывают значения DN_i/Dr_i и строят дифференциальную кривую распределения, пример которой показан на рис. 2.66, б. На оси абсцисс строят прямоугольники со стороной от r_i до r_i+1, а высотой, равной DN_i/Dr_i. Середины прямоугольников соединяют между собой, в результате чего получается дифференциальная кривая распределения с максимумом, соответствующим 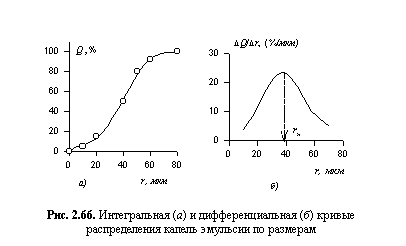наиболее вероятному размеру капель.

Распределение капель в эмульсиях выражают также зависимостью удельной поверхности и объема капель от их размера. Удельную поверхность и объем всех капель рассчитывают после нахождения среднеобъемного и среднеповерхностного радиусов. После расчета среднего объема капель по формуле

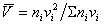(2.7.16)

находят среднеобъемный радиус

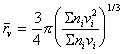. (2.7.17)

Среднеповерхностный радиус определяют по формуле

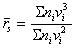. (2.7.18)

Удельную поверхность капель рассчитывают по формуле

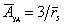. (2.7.19)

Кривые распределения по поверхности и объему строятся аналогично кривым распределения по массе или числу капель.

Расчет данных для построения кривых поверхностного и объемного распределения проводят по следующим уравнениям:

объем капель фракции i

V_i = (4/3)pr³_i , (2.7.20)

поверхность капель фракции i

А_i = pr²_i , (2.7.21)

поверхностная доля капель фракции i

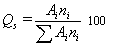, (2.7.22)

объемная доля капель фракции i

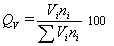, (2.7.23)

Обычно наиболее вероятный радиус, определяемый из абсциссы максимума дифференциальных кривых распределения числа частиц по размерам, поверхности и объему не совпадают.