2.3.2. Броуновское движение
В 1826 г. ботаник Р. Броун, наблюдая под микроскопом взвесь в виде растительной пыльцы (ликоподия), обнаружил, что частицы находятся в непрерывном движении, получившем название «броуновского». Он установил, что частицы не только перемещаются поступательно, но и поворачиваются вокруг своих осей, совершая вращательное движение. Броун проверил свои наблюдения на большом числе объектов и высказал ряд предположений относительно этого явления (так как в то время еще не существовало молекулярной теории строения вещества). Многие исследователи считали, что причиной броуновского движения являются внешние силы, а не внутренние – молекулярное движение жидкости.
Молекулярно-кинетические расчеты показывают, что коллоидные частицы способны проделывать элементарный путь l длиной 4·10-10 м за время 3·10-10 с.
В 1903 г. Р. Зигмонди и Зидентопф сконструировали ультрамикроскоп и с его помощью установили, что мелкие частицы находятся в еще более, чем крупные, интенсивном движении. Эти частицы не только колеблются около одного центра, но и совершают зигзагообразное движение. Движение крупных частиц более сложно, чем мелких, так как масса такой частицы намного превосходит массу молекул и, следовательно, каждое столкновение с движущимися молекулами отклоняет частицу на ничтожно малое расстояние.
Даже при наблюдении в ультрамикроскоп можно увидеть только суммарные пути за определенный промежуток времени. Наименьшее наблюдаемое человеком время 0,1 с, поэтому путь, составляющий длину пробега частицы, равен 107l, т.е. 10 млн. элементарных движений, следовательно, возможность наблюдения элементарного пути исключается. Поэтому рассматривают средний сдвиг частицы 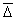
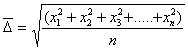 , (2.2.87)
, (2.2.87)
где xi– элементарное смещение частицы по оси x.
В 1905-1908 гг. А. Эйнштейн и М. Смолуховский независимо друг от друга разработали теорию броуновского движения. В основе теории заложены следующие предпосылки:
– кинетическая энергия частицы, взвешенной в жидкости или газе, соответствует средней кинетической энергии молекул;
– экспериментатор может не считаться с фактически пройденным частицей путем или с фактической скоростью частицы, он может ограничиться средним смещением частицы за определенное время.
Вывод уравнения Эйнштейна - Смолуховского проводят следующим образом.
|
Представим мысленно плоскость М, проходящую через золь (рис. 2.14). Предположим, что концентрация С1 в левой части больше концентрации С2 в правой части. Коллоидные частицы в обеих частях системы совершают броуновское движение. Причина этого движения заключается в разности импульсов, полученных частицей с противоположных сторон. Естественно, чем меньше частица, тем менее вероятность компенсации импульсов и, следовательно, тем интенсивнее броуновское движение. Для частиц одинакового размера при определенной температуре среднее перемещение 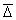 по направлению оси x влево или вправо за время t будет одинаковым. Следовательно, число частиц, которые пройдут расстояние от плоскости 1 до плоскости М, будет равно
по направлению оси x влево или вправо за время t будет одинаковым. Следовательно, число частиц, которые пройдут расстояние от плоскости 1 до плоскости М, будет равно 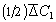 . Число частиц, проходящих от плоскости 2 до плоскости М, будет равно
. Число частиц, проходящих от плоскости 2 до плоскости М, будет равно 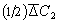 , в результате через плоскость за время t будет перенесено
, в результате через плоскость за время t будет перенесено 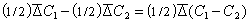 вещества. Если
вещества. Если 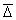 достаточно мало (или, что то же самое – мало время t), то
достаточно мало (или, что то же самое – мало время t), то
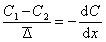 или
или 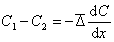 (2.2.88)
(2.2.88)
(знак минус ставится по тем же причинам, что и в уравнении Фика).
Следовательно, очевидно, что количество вещества, перенесенного за 1 с, составит
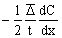 . (2.2.89)
. (2.2.89)
Если площадь плоскости М равна 1, то уравнение (2.2.89) перейдет в уравнение для диффузионного потока
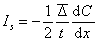 . (2.2.90)
. (2.2.90)
Сравнивая его с уравнением закона Фика, видим

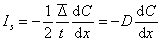 . (2.2.91)
. (2.2.91)
Поэтому 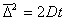 , но
, но
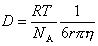 . (2.2.92)
. (2.2.92)
Cледовательно,
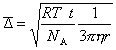 . (2.2.93)
. (2.2.93)
Из уравнения (2.2.93) видно, что 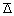 пропорционален t1/2.
пропорционален t1/2.
Справедливость этого уравнения подтвердил Сведберг, фотографируя коллоидные частицы через ультрамикроскоп. Он исследовал монодисперсный золь золота и получил очень хорошие результаты, рассчитывая число Авогадро по измеренным экспериментально 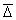 для частиц с известным r.
для частиц с известным r.
Другой метод проверки уравнения основан на использовании частиц одного и того же вещества, но в разных дисперсионных средах с различной вязкостью. Тогда
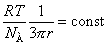 , (2.2.94)
, (2.2.94)
поэтому
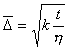 или
или 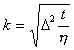 . (2.2.95)
. (2.2.95)
Сведберг изучал движение частиц платины в ацетоне, этилацетате, амилацетате, воде, нормальном пропиловом спирте, т.е. в жидкостях с различными значениями вязкости h. Таким образом, Сведберг экспериментально подтвердил справедливость уравнения Эйнштейна-Смолуховского, полученного теоретически.
Перрен воспользовался суспензией частиц гуммигута (сгущенного млечного сока каучуконосных деревьев) и провел ряд наблюдений броуновского движения частиц через микроскоп со специальным приспособлением. Через равные промежутки времени отмечалось положение частиц. На основании полученных данных проводилось вычисление числа Авогадро. Найденное значение составило NА = 6,5×1023. Эти опыты стали окончательным доказательством молекулярно-кинетической теории строения материи.
Вместо того, чтобы измерять смещение отдельных частиц, можно определять число частиц в определенном малом объеме, который сообщается с большим объемом. Оказывается, что число частиц в таком микроскопическом объеме непрерывно меняется, хотя, согласно второму закону термодинамики, должно было быть равным и постоянным в любой момент времени.
Если рассматривать малый объем, то число частиц будет небольшим и его можно подсчитать. Если производить подсчет числа частиц через некоторое время, то окажется, что это число не постоянно. Такое изменение числа частиц в малом объеме носит название флуктуации. Теория этого явления была разработана Смолуховским и проверена им на результатах исследования золей Сведбергом. Теория флуктуации также определяет границы применимости второго начала термодинамики.

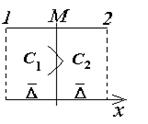 Рис. 2.14. Схема, поясняющая вывод уравнения Эйнштейна - Смолуховского
Рис. 2.14. Схема, поясняющая вывод уравнения Эйнштейна - Смолуховского
