Теория Фишера

Рассмотренные выше теории стерической стабилизации основаны на произвольных допущениях. В частности предполагалось, что экспериментальные значения среднеквадратичного расстояния между концами макромолекул в адсорбированном состоянии соответствуют этой характеристике для свободных макромолекул в растворах. Кроме того, не учитывалась действительная толщина адсорбционно-сольватных оболочек.

В этой связи практическое применение рассмотренных выше теорий до настоящего времени остается ограниченным.

Чаще всего для расчетов стабилизирующего действия полимеров используют уравнение Фишера, предложенное им в 1959 г. В этом уравнении теоретический расчет функции распределения звеньев (хвостов или петель) макромолекул в зазоре между частицами заменен эмпирической величиной параметра взаимодействия, определяемого из осмотического давления растворов полимеров.

Фишер рассматривал изменение энергии Гиббса в объеме перекрытия адсорбционно-сольватных слоев в соответствии с изменением концентрации растворителя как

d (D^(s)G^(a)) = (D^(s) G^(a) / n₁) dn₁ , (2.3.85)

где n₁-число молекул растворителя.

Частная производная в скобках уравнения (2.3.85) характеризует изменение химического потенциала (Dm₁ = m₁ – m₁⁰ ) молекул растворителя при переносе n_i их из объема раствора в адсорбционно-сольватную оболочку и определяется избыточным осмотическим давлением

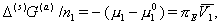(2.3.86)

где p_E – избыточное осмотическое давление; 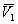– парциальный молярный объем растворителя; n_i – число молекул растворителя, перенесенных из объема раствора в область перекрытия оболочек частиц.

Знак «минус» в уравнении (2.3.86) обозначает концентрирование раствора при перекрытии адсорбционно-сольватных оболочек частиц.

Можно отметить, что уравнение Фишера базируется на идее Ленгмюра об осмотической природе сил отталкивания, возникающих при перекрытии стабилизирующих слоев.

Подставляя выражение (2.3.86) в уравнение (2.3.85) и учитывая, что 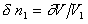, получаем

d (D^(s)G^(a)) = p_EdV. (2.3.87)

Интегрируя это уравнение в пределах от dV = 0 до V и учитывая перекрытие двух слоев введением множителя «2», получаем

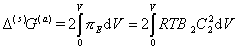, (2.3.88)

где B₂ – второй вириальный коэффициент; C₂ – концентрация полимера в адсорбционном слое.

Фишер полагал, что избыточное осмотическое давление при перекрытии адсорбционно-сольватных оболочек определяется исключительно изменением межмолекулярного взаимодействия, поэтому после разложения в ряд зависимости осмотического давления от концентрации он ограничивался учетом только второго члена разложения. Такое ограничение предполагает, что для макромолекул вклад первого члена разложения пренебрежимо мал, так как он связан с подвижностью макромолекул как единого целого. Кроме того, Фишер принял равномерное распределение макромолекул по всему объему адсорбционно-сольватных оболочек.

С учетом этих ограничений Фишер получил уравнение

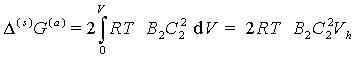, (2.3.89)

где V_h– объем перекрытия адсорбционно-сольватных слоев при сближении частиц на расстояние h.

Для сферических частиц этот объем можно рассчитать по уравнению

V_h = (2/3)p(D – h/2)² (3r + 2D + h/2), (2.3.90)

где D– толщина адсорбционно-сольватной оболочки, h – наименьшее расстояние между поверхностями частиц радиуса r.

Второй вириальный коэффициент необходимо определять экспериментально для растворов полимеров, имеющих концентрацию, соизмеримую с их концентрацией в адсорбционном слое. Его можно также рассчитать по уравнению теории растворов полимеров Флори - Хаггинса

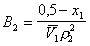, (2.3.91)

где 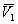– парциальный молярный объем растворителя; r₂ – плотность полимера в растворе, которую определяют по величине парциального удельного объема полимера.

Уравнение Фишера не учитывает упругой энергии отталкивания, которая начинает проявляться на расстояниях, меньших толщины адсорбционно-сольватных слоев.

Для расчета энергии отталкивания кроме знания второго вириального коэффициента необходимо экспериментальное определение толщины адсорбционно-сольватных оболочек и концентрации полимера в них, что возможно при изучении адсорбции полимера на частицах и вискозиметрическом исследовании сольватации.

Более точные расчеты возможны, если кроме средней концентрации полимерных молекул в адсорбционно-сольватных оболочках удается определить вид их распределения. Чаще всего его экспериментальное определение оказывается невозможным, поэтому расчет проводят при использовании предпосылки равномерного распределения (1), радиальной функции распределения Гаусса (2) или экспоненциальной функции распределения. Расчет показывает, что некоторое различие энергии отталкивания, рассчитанной с привлечением модели экспоненциального распределения, наблюдается на расстояниях, меньших длины вытянутой цепи макромолекул. Модели гауссова распределения и модели равномерного распределения предсказывают близкий характер зависимости энергии отталкивания от объема перекрытия адсорбционционно-сольватных оболочек. В этой связи удобнее пользоваться теорией Фишера для дисперсий, стабилизированных неионогенными полимерами.

Для расчета по уравнению (2.3.89) энергии отталкивания кроме знания второго вириального коэффициента необходимо экспериментальное определение толщины адсорбционно-сольватных оболочек и концентрации полимера в них, что возможно при изучении адсорбции полимера на частицах и вискозиметрическом исследовании их сольватации.