3.3.4. Стабилизация неионогенными поверхностно-активными веществами

Неионогенные поверхностно-активные вещества являются великолепными стабилизаторами гидрофобных дисперсных систем и поэтому находят широкое применение в синтезе латексов и при стабилизации дисперсий пигментов в водной среде. После формирования на поверхности частиц лиофильного слоя стабилизатора такие дисперсии становятся лиофилизированными и устойчивыми в присутствии больших количеств электролитов, вплоть до их концентрации в несколько кмоль/м³.

Проведенные Зонтагом расчеты значений постоянной Гамакера для частиц, на поверхности которых сформирован адсорбционный слой, показали, что энергия притяжения частиц изменяется незначительно при формировании адсорбционно-сольватных слоев этих стабилизаторов. В то же время электрокинетический потенциал после адсорбции неионогенных ПАВ снижается в результате смещения плоскости скольжения от поверхности дисперсной фазы в глубь раствора. Равновесная толщина адсорбционных слоев достигает величины от 10 до 20 нм в зависимости от степени оксиэтилирования стабилизатора и его концентрации в адсорбционно-сольватных слоях.

Применение уравнения Фишера для таких систем целесообразно только для случая полимерных стабилизаторов, для которых можно пренебречь первым вириальным членом разложения зависимости осмотического давления от концентрации адсорбированного вещества. Для низкомолекулярных неионогенных ПАВ уравнение Фишера дает большую погрешность в расчетах стерической энергии отталкивания частиц при их сближении.

Этомуесть две причины:

1) идеальное приближение, лежащее в основе вывода формулы Фишера, исключает из рассмотрения разность осмотических давлений, возникающих вследствие различия концентраций растворенного вещества в объеме дисперсионной среды и в адсорбционно-сольватном слое;

2) определение второго вириального коэффициента методом светорассеяния и осмотического давления в мицеллярных растворах неионогенных ПАВ характеризует в большей степени не параметр взаимодействия между растворителем (водой) и растворенным веществом, а форму мицелл.

Поэтому такой метод иногда дает отрицательное значение второго вириального коэффициента даже для растворов ПАВ с интенсивной гидратацией молекул и увеличение второго вириального коэффициента при снижении гидратации с ростом температуры. Естественно, что привлечение таких данных к расчету устойчивости дисперсных систем может привести только к искажению действительной картины и к получению заведомо неверных результатов. Поэтому для характеристики устойчивости необходимо определять взаимодействие между ПАВ (стабилизатором) и дисперсионной средой непосредственно в адсорбционных слоях, что позволяет исключить эффект отклонения формы частиц от сферической.

Систематическое исследование гидратации неионогенных ПАВ в мицеллярных системах, адсорбционных слоях и непосредственно частиц с адсорбционными или локализованными химическим путем слоями стабилизатора позволило выявить важную роль гидратных оболочек в стабилизации дисперсных систем. Обширный экспериментальный материал позволил провести также количественную оценку стабилизирующего действия сольватных оболочек при различных условиях существования дисперсных систем – нагревании, введении электролитов. Для расчета молекулярной составляющей расклинивающего давления можно использовать уравнение, полученное в работах В.А. Волкова на основании представлений Ленгмюра об осмотической природе стабилизирующего действия тонких адсорбционно-сольватных слоев.

Если рассматривать системы из гидрофобных частиц в водной среде, стабилизированные неионогенными стабилизаторами без специфического взаимодействия гидрофильных групп стабилизатора с поверхностью частиц, то можно ограничиться случаем ориентации адсорбционного слоя гидрофобными радикалами к поверхности частиц, а гидрофильными группами – в сторону водной дисперсионной среды.

При введении n молей поверхностно-активного вещества в водную фазу дисперсной системы произойдет распределение его между объемной фазой и поверхностью частиц таким образом, что 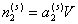молей ПАВ будет оставаться в растворе, а 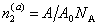– на поверхности раздела фаз. Здесь 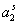- активность ПАВ в водной фазе; V – объем дисперсионной среды, А – общая площадь поверхности частиц с избыточной удельной свободной энергией s ; A₀ – площадь молекулы в адсорбционном слое; N_А – число Авогадро.

Очевидно, что концентрирование ПАВ на поверхности (адсорбция) будет протекать до тех пор, пока вся поверхность частиц не будет изолирована от водной среды. Процесс будет происходить до выравнивания химических потенциалов ПАВ и растворителя в различных частях системы.

При равновесии

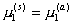, (2.3.92)

но

m= m⁰ + RT ln a, (2.3.93)

поэтому

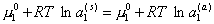. (2.3.94)

Принимая за стандартное состояние «чистую» воду, т.е. при (a₁ = 1), записываем

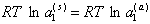(2.3.95)

или

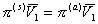, (2.3.96)

так как

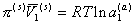(2.3.97)

и

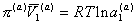, (2.3.98)

где индексы (s) и (a) соответственно относятся к объемной и поверхностной фазам.

Для разбавленных растворов, т.е. для дисперсионной среды ограничимся только первым членом разложения в ряд

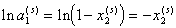. (2.3.99)

Поэтому

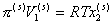, (2.3.100)

или

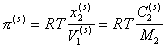, (2.3.101)

где 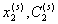- концентрация растворенного ПАВ, выраженная соответственно в молярных долях и в (г/см³); V₁– парциальный молярный объем воды; M₂– молекулярная масса растворенного вещества.

Для концентрированных растворов (адсорбционно-соль­ватных оболочек) с учетом взаимодействия между молекулами необходимо учитывать два члена разложения, поэтому

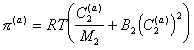. (2.3.102)

При осмотическом равновесии p^(s) = p^(a), а так как 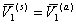, то

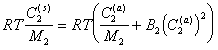(2.3.103)

или

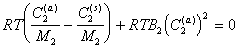. (2.3.104)

Осмотическое равновесие может быть смещено при изменении условий:

1. При повышении температуры изменяется взаимодействие между молекулами в адсорбционном слое, т.е. изменяется второй вириальный коэффициент B₂ , что повлечет перераспределение растворителя между объемной и поверхностной фазами (раствором и адсорбционно-сольватными оболочками).

2. Введение дополнительных количеств ПАВ (сверх концентрации, соответствующей пределу адсорбции) или любого другого вещества в раствор, т.е. увеличение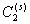, также вызовет смещение равновесия, причем для его восстановления при B₂ = const потребуется увеличение 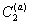, а это возможно только в результате дегидратации частиц, так как адсорбция сверх предельной величины G_m невозможна. Поэтому добавление стабилизатора в концентрациях, превышающих равновесную при пределе адсорбции, должно приводить к уменьшению количества связанной в сольватные оболочки воды и, следовательно, к снижению стабильности дисперсной системы. Экспериментальные данные действительно указывают на такой эффект, когда добавление стабилизатора сверх предела насыщения поверхности частиц может приводить к снижению толщины гидратных оболочек. Аналогичный эффект должен наблюдаться при введении любого вещества, например, электролита или низкомолекулярного неэлектролита.

Таким образом, в дисперсных системах с адсорбированными молекулами неионогенного ПАВ на поверхности частиц равновесная толщина стабилизирующей сольватной оболочки определяется температурой и концентрацией растворенного в дисперсионной среде вещества. Варьируя эти условия можно сместить равновесие вплоть до полной дегидратации поверхности частиц и нарушения агрегативной устойчивости дисперсных систем, в которых в качестве стабилизатора использованы неионогенные ПАВ.

Коагуляция таких систем может протекать как при нагревании, так и при введении любых растворимых в воде веществ.

Слипание частиц в дисперсных системах с адсорбционно-сольватными оболочками возможно только в том случае, если целостность этих оболочек будет нарушена и частицы получат возможность образовывать непосредственный контакт. Если этот процесс проводить целенаправленно, то для этого надо совершить работу по смещению осмотического равновесия, описываемого уравнением (2.3.104). Рассматривая парное взаимодействие частиц, эту работу можем выразить в соответствии с уравнением (2.3.88) как

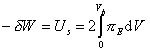, (2.3.105)

где V_h – объем перекрытия адсорбционно-сольватных оболочек при сближении частиц на расстояние h< 2D,D - толщина адсорбционно-сольватной оболочки.

Следовательно, dW- это работа концентрирования раствора в элементе объема dV сольватных оболочек частиц. Эта работа будет направлена на преодоление избыточного осмотического давления p_E, но не на десорбцию стабилизатора (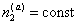). Тогда в соответствии с (2.3.104) энергия, которую следует затратить на сближение частиц, т.е. энергия отталкивания частиц при их равновесном сближении, будет

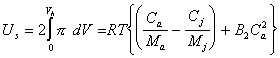, (2.3.106)

где С_a - концентрация стабилизатора в адсорбционно-сольватном слое; С_j - суммарная концентрация всех видов веществ в растворе.

Объем перекрытия адсорбционно-сольватных оболочек V_h рассчитывают по следующим уравнениям:

– для сферических частиц одинакового размера (радиус частиц r)

V_h = (2/3) p (D – h/2)² (3r+2D+ h/2); (2.3.107)

– для сферической частицы радиуса r и бесконечной плоской частицы

V_h=(p/3) (2D- h)2 (3r+D+ h); (2.3.108)

– для взаимодействия двух плоских бесконечных пластин (в расчете на единицу площади поверхности)

V_h = 2 (2D – h), (2.3.109)

где h – наименьшее расстояние между поверхностями частиц, D– толщина адсорбционно-сольватной оболочки частиц.

Из уравнения (2.3.106) следует, что расклинивающее давление адсорбционно-сольватных оболочек состоит из двух компонент:

1) концентрационной компоненты, связанной с разностью концентраций растворенного вещества в объеме перекрытия адсорбционно-сольватных оболочек и в объеме дисперсионной среды;

2) структурной компоненты, связанной с изменением интенсивности межмолекулярного взаимодействия ПАВ и воды при концентрировании адсорбированных молекул при перекрытии адсорбционно-сольватных оболочек.

Как мы отмечали уже выше, использованные при расчете потенциальной энергии отталкивания второго вириального коэффициента, найденного для растворов неионогенных ПАВ с концентрацией, соответствующей таковой в адсорбционных слоях, может привести к неправильным результатам, поэтому с целью исключения неопределенности в расчетах проводят дальнейшее преобразование уравнения (2.3.106). Для этого используется соотношение между вторым вириальным коэффициентом и характеристической вязкостью, которое для хороших растворителей имеет вид

B₂M₂ / [h] = 1,0 . (2.3.110)

Для незаряженных частиц справедливо уравнение

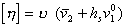, (2.3.111)

где [h] – характеристическая вязкость; u – коэффициент формы частиц Симха – Эйнштейна (для сфрических частиц u= 2,5); 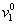- удельный объем воды; h_s – удельная гидратация частиц (г Н₂О/г ПАВ), – парциальный объем стабилизатора.

Таким образом

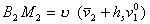. (2.3.112)

Поэтому

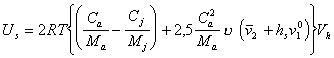. (2.3.113)

Как было установлено, гидратация в мицеллах и адсорбционных слоях ПАВ одинакова, поэтому можно гидратацию выразить в удельных единицах по отношению к дисперсной фазе

W_h = h_s W_e , (2.3.114)

где W_h - удельная гидратация частиц [г Н₂О/г полимера (дисперсной фазы)], W_e – массовая доля стабилизирующего ПАВ в дисперсной фазе.

Так как в дисперсных системах, например, в латексах, полученных методом конденсации частицы, а следовательно, и адсорбционно-сольватные оболочки имеют сферическую форму, поэтому u = 2,5. Тогда

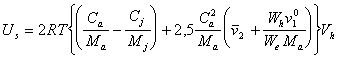. (2.3.115)

Из уравнения (2.3.115), с учетом, что 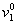» 1, и выражая среднюю массовую концентрацию стабилизатора C_а (г ПАВ / см³) в адсорбционно-сольватной оболочке как C_а = 1/h_s= W_e / W_h, получаем

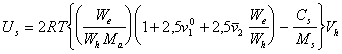. (2.3.116)

При определении гидратации частиц по результатам изучения явлений переноса часто полагают, что `v₂ = 1, поэтому

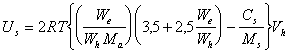(2.3.117)

или

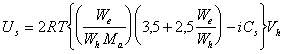, (2.3.118)

где C_s – концентрация всех видов растворенных веществ в дисперсионной среде (моль/л); i – изотонический коэффициент, который необходимо учитывать для растворов электролитов.

Условие 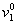» 1 для воды соблюдается в области температур до 263 К. Условие v₂ = 1 можно считать корректным для неионогенных ПАВ со степенью оксиэтилирования 10-20 в области температур до 350 К. Для неионогенных ПАВ со степенью оксиэтилирования меньше 10, v₂ = 0,8¸0,9, поэтому в дисперсных системах с такими стабилизаторами при расчетах необходимо учитывать отклонение v₂ от единицы.

Совмещение уравнений (2.3.22) для энергии притяжения и (2.3.115) для энергии отталкивания при перекрытии адсорбционно-сольватных оболочек позволяет расчитать сольватационную составляющую расклинивающего давления и общую потенциальную энергию взаимодействия частиц U_T.

Критерием устойчивости следует считать условие

U_T = U_s + U_m > 0, (2..3.119)

где U_m – энергия притяжения, которая для сферических частиц может быть определена по уравнению (2.3.22):

U_m = - A^* r/12 h ,

где A^* – постоянная межмолекулярных сил притяжения Гамакера, r – радиус частиц, h – наименьшее расстояние между частицами.