Современные теории стерической стабилизации
Теория Мейера

В теории Мейера, описанной впервые им в 1967 г., учитывались два процесса, возможные при перекрытии адсорбционно-сольватных оболочек. Первый из них, также как и в теории Ёкеля – упругие эффекты при взаимодействии частиц, второй – эффект смешения полимерных цепей при перекрытии адсорбционно-сольватных оболочек.

Для смешения полимерных цепей молекул, закрепленных одним концом на поверхности, в ограниченном объеме между двумя непроницаемыми бесконечными пластинами был использован принцип диффузии цепей мекромолекул из адсорбционного слоя одной поверхности в элементарный объем адсорбционного слоя другой поверхности при их сближении.

В основу теории было положено уравнение Ямакавы

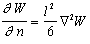, (2.3.62)

где W – вероятность заданного расстояния между концами цепи полимерной молекулы с n звеньями, каждое из которых имеет длину l, 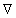– градиент плотности сегментов.

Расчет по этому уравнению не учитывал эффекта исключенного объема при повышении плотности упаковки цепей в зазоре между сближающимися частицами и поэтому его следует считать оценочным.

Расчет изменения свободной энергии смешения полимерных сегментов и молекул растворителя при перекрытии адсорбционно-сольватных оболочек с объемом перекрытия dV проводится с привлечением теории растворов полимеров Флори-Хаггинса, в соответствии с которой

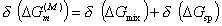, (2.3.63)

где DG_mix – изменение энергии Гиббса при смешении молекул полимера и растворителя без учета межмолекулярных взаимодействий, определяемое из геометрического анализа возможных размещений цепей в условных ячейках раствора; DG_sp– изменение свободной энергии при смешении в результате изменения межмолекулярных взаимодействий.

Из статистического рассмотрения смешения молекул растворителя и звеньев макромолекул в соответствии с теорией Флори-Хаггинса следует для комбинированного вклада

d (DG_mix) = kT (dn₁ lnj₁ + dn₂ lnj₂), (2.3.64)

где dn₁, dn₂ – изменение числа молекул растворителя и полимерных звеньев в элементарном объеме перекрытия адсорбционно-сольватных оболочек dV;j₁,j₂ – объемные доли растворителя и полимерных звеньев.

Для второго члена контактного вклада в уравнении (2.3.63) теория Флори-Хаггинса дает

d (DG_sp) = kT C₁ (dn₁)j₂ , (2.3.65)

где C₁– параметр межмолекулярного взаимодействия, экспериментально найденный при объемной доле полимера j₂.

Учитывая, что j₁ = (1-j₂),dn₂ = -dn₁и lnj₂<< ln(1-j₂),получаем из уравнений (2.3.64) и (2.3.65) для изменения энергии Гиббса смешения

d (DG^(M)) = kT(lnj₁-lnj₂ + x₁j₂)dn₁ = kT[ln(1-j₂) + xj₂]dn. (2.3.66)

Разлагая в ряд ln(1-j₂) = -j₂ - (1/2) j₂²и ограничиваясь только двумя членами разложения, записываем

d(DG^(M)) = kT( x₁j₂ - j₂- 0,5 j₂²)dn₁. (2.3.67)

Поскольку

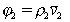(2.3.68)

и

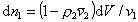, (2.3.69)

где r₂ – плотность (число) сегментов в единице объема раствора, 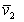– парциальный удельный объем сегмента полимера, v₁ - объем молекулы растворителя, то из уравнения (2.3.66) с учетом, что 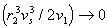, следует

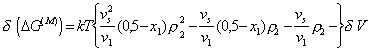. (2.3.70)

Уравнение (2.3.70) является фундаментальным уравнением для растворения аморфного полимера, локализованного на поверхности частиц. Первый член в правой части уравнения (2.3.70) учитывает изменение конформации макромолекул в зазоре между частицами; второй член учитывает изменение качества растворителя и изменение энергии межмолекулярного взаимодействия; третий член описывает изменение растворимости при неизменной конформации цепей макромолекул.

Изменение свободной энергии при смешении находят после интегрирования уравнения (2.3.70) в пределах от dV = 0 до V. Считается, что линейные члены при таком интегрировании остаются неизменными в связи с тем, что интеграл 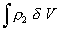имеет смысл общего числа сегментов и не будет зависеть от расстояния между частицами. Поэтому после интегрирования все линейные члены уравнения (2.3.70) обращаются в нуль и остаются лишь квадратичные члены, поэтому

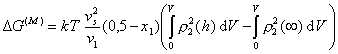. (2.3.71)

Второй член в уравнении (2.3.71) в квадратных скобках учитывает полную свободную энергию смешения полимерных молекул с молекулами растворителя в растворе до перекрытия адсорбционно-сольватных оболочек.

Уравнение (2.3.71) используют в качестве базового при рассмотрении различных случаев перекрытия адсорбционно-соль­ватных слоев, например, для двух пластин бесконечной площади, сферических частиц и т.д.

Для плоских частиц уравнение (2.3.71) записывают в виде

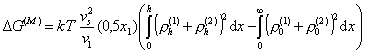,(2.3.72)

где 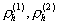– плотность сегментов полимерных молекул, адсорбированных на поверхности частиц 1 и 2, соответственно.

Предполагается, что плотность в любой плоскости, параллельной поверхности частиц, остается постоянной. Такое допущение позволяет перейти от интегрирования по объему перекрытия к интегрированию по расстоянию между частицами и отнести изменение свободной энергии при сближении частиц к единице площади их поверхности.

Принимая, что

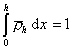, (2.3.73)

где 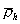– удельная плотность сегментов, и учитывая, что

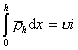, (2.3.74)

где u– число полимерных цепей на единице площади поверхности частиц, i-число звеньев в полимерной цепи (считается, что звено полимерной молекулы имеет размер, соизмеримый с размером молекулы растворителя), из уравнений (2.3.73) и (2.3.74) можем записать

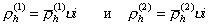, (2.3.75)

а для единицы поверхности частиц

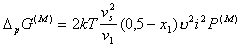, (2.3.76)

где P^(М)- обозначает параметр распределения плотности полимерных цепей в зазоре между частицами, который определяется как

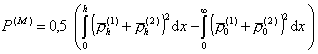. (2.3.77)

Обозначая термодинамический параметр в уравнении (2.3.76) как U ,

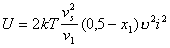, (2.3.78)

можем записать

D_pG^(M) = UP^(M). (2.3.79)

Уравнение (2.3.79) представляет собой частный случай для частиц с плоской поверхностью общего уравнения

DG^(M) = g U S, (2.3.80)

где g – коэффициент формы частиц; S – параметр пространственного распределения цепей в зазоре между частицами.

Уравнения (2.3.79) и (2.3.80) не учитывают вклада упругого сжатия. Уравнение для расчета этого вклада предложил Мейер. Он использовал уравнение Ямакавы для расчета вероятности распределения цепей и уравнение Больцмана для определения энтропии

DG^(el) = -TDS = - 2nkT lnP_n (h) , (2.3.81)

где P_n(h) – вероятность размещения элементов цепей в зазоре между частицами, множитель 2 учитывает наличие двух поверхностей.

Практический расчет функции P_n представляет значительную трудность. Дальнейшее развитие теории Мейера было проведено в работах Хесселинка, который предложил следующее уравнение для свободной энергии отталкивания плоских частиц с адсорбированными цепями полимерных молекул

D^(p)G^(a) = (4p/9)^3/2n²kT(a²-1) <r²> M(h) + 2nkTV(h), (2.3.82)

где <r²> – среднеквадратичное расстояние между концами полимерной цепи; a - степень набухания клубков; М(h) – функция осмотического отталкивания ; V(h)- функция ограничения объема.

Для сферических частиц было получено уравнение

D_(s)G_(a) = [(2/27) p^5/2]n² kT a <r²> (a² – 1) S^(M), (2.3.83)

где a – радиусчастиц;

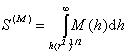. (2.3.84)

Эта функция для сферических частиц табулирована.

Расчет упругого вклада показал, что для сферических частиц его роль несоизмеримо мала по отношению к вкладу смешения и поэтому его не учитывают.

Последующее развитие теория отталкивания частиц дисперсной фазы, стабилизированных полимерными молекулами, была развита в работах Эдвардса и Долина. В этих работах нет того искусственного разделения энергии Гиббса при стерическом взаимодействии, как это было сделано в теориях Майера и Хеселинка, в них использовался принцип исключенного объема при взаимодействии сегментов макромолекул.

Полученные уравнения оказались бесполезными для практических расчетов и поэтому мы не будем их здесь рассматривать. Желающие углубить свои знания в этой области коллоидной науки могут ознакомиться с их изложением по монографии Наппера.