6.8.3. Комбинированный метод измерения диффузии и вязкости

Вторым по широте применения (после метода светорассеяния) является комбинированный метод измерения диффузии и вязкости.

Если считать, что мицелла перемещается как самостоятельная кинетическая единица в ньютоновской жидкости, то сила внутреннего трения пропорциональна скорости:

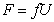. (2.6.26)

Здесь коэффициент пропорциональности fносит название коэффициента трения.

Для сферических мицелл, перемещающихся на большом расстоянии от стенок сосуда, справедливо соотношение Стокса

f=6ph₀r, (2.6.27)

где h₀- вязкость растворителя, r- радиус мицеллы.

Уравнение (2.6.27) справедливо при скорости перемещения сферических мицелл 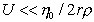, где r- плотность растворителя.

Коэффициент трения связан с коэффициентом диффузии уравнением Эйнштейна

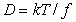(2.6.28)

или

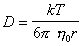. (2.6.29)

Если мицелла имеет сферическую форму, то ее объем .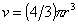

Умножив объем одной мицеллы на плотность ПАВ и число Авогадро, получаем «мицеллярную» молекулярную массу:

,

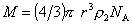откуда

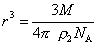. (2.6.30)

Подставляя полученное выражение в уравнение (2.6.29), получаем

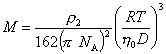. (2.6.31)

Использование этого уравнения для определения мицеллярной молекулярной массы однако затруднено вследствие того, что плотность мицелл может существенноотличаться от плотности пав в конденсированном состоянии. Поэтому в уравнение (2.6.31) необходимо ввести величину эффективной плотности или эффективного гидродинамического удельного объема v_ef, тогда

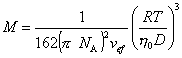. (2.6.32)

Эффективный объем растворенного вещества можно определить из вискозиметрических данных. Используя уравнение Симха для сферических частиц,

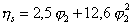, (2.6.33)

где h_s-удельная вязкость, j₂- объемная доля растворенного вещества, и выражая концентрацию растворенного вещества с₂ в граммах на кубический сантиметр, найдем выражение для объемной доли, 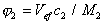, где М₂ – молекулярная масса растворенного вещества. Учитывая это соотношение, уравнение (2.6.33) может быть записано в виде

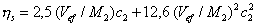, (2.6.34)

где V_ef - эффективный гидродинамический мольный объем.

Если применять обычные обозначения, то

, (2.6.35)

где [h] -характеристическая вязкость, см³/ г; K¢- постоянная Хаггинса.

Для сферических мицелл постоянная Хаггинса K¢ должна иметь значение, близкое к 2,0. Возникновение асимметричных мицелл может привести к увеличению или уменьшению постоянной K¢.

Таким образом, задача сводится, прежде всего, к определению формы мицелл, для чего по зависимости приведенной вязкости 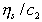от концентрации определяется постоянная Хаггинса. После этого находится значение удельного эффективного гидродинамического объема, так как согласно уравнений (2.6.34) и (2.6.25) для сферических частиц .

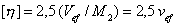Затем, используя уравнение (2.6.32), по известной постоянной диффузии рассчитывается мицеллярная молекулярная масса.

Таким образом, использование комбинированного метода измерения диффузии и вязкости ограничено растворами ПАВ, содержащими сферические мицеллы.

Кроме того, для получения достаточно корректных результатов необходимо вводить поправки на присутствие молекулярно-растворенного ПАВ.