1.2. Образование коллоидных систем при конденсации пара
Возникновение новый фазы из маточной происходит с образованием капель или частиц, в которых количество молекул, находящихся на поверхности раздела фаз соизмеримо с их количеством в объеме частиц (капель). В связи с этим уже нельзя пренебрегать свойствами молекул на поверхности раздела. Именно этими свойствами и определяется степень метастабильности системы, т.е. высота максимума на изотерме диаграммы P - V, например abcd рис. 2.1. Степень пересыщения, при которой возникают частицы новой фазы, определяется отклонением давления P от равновесного давления фазового перехода P0, поскольку при фазовом равновесии, т.е. при mж = mп, где ж и п – соответственно обозначают жидкость и пар, при возрастании давления от Р0 до Р в паре химический потенциал mп равен
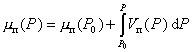 . (2.1.4)
. (2.1.4)
Полагая, что пар может подчиняться уравнению Клайперона-Менделеева 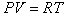 , можем записать
, можем записать
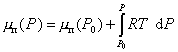 , (2.1.5)
, (2.1.5)
откуда
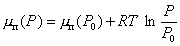 . (2.1.6)
. (2.1.6)
Химический потенциал жидкости равен
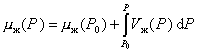 . (2.1.7)
. (2.1.7)
Считая, что жидкость не сжимается в интервале давлений от Р0 до Р, т.е. Vж = const, получаем
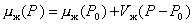 . (2.1.8)
. (2.1.8)
Степень пересыщения определяется разностью химических потенциалов пара и жидкости
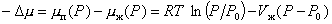 . (2.1.9)
. (2.1.9)
Молярный объем паровой фазы существенно больше молярного объема жидкости, т.е. Vп > Vж, поэтому
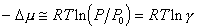 . (2.1.10)
. (2.1.10)
Отношение 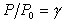 и есть пересыщение пара. Здесь Р – давление, при котором образуются частицы (капли) новой фазы; Dm - уравновешивает избыточную свободную энергию.
и есть пересыщение пара. Здесь Р – давление, при котором образуются частицы (капли) новой фазы; Dm - уравновешивает избыточную свободную энергию.
Действительно, свободная энергия диспергирования DGd равна работе образования поверхности одной частицы
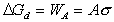 , (2.1.11)
, (2.1.11)
где А = 4p r2 – площадь поверхности сферической частицы радиуса r; s – удельная свободная энергия поверхности.
Свободная энергия DGV, равная работе переноса n молей вещества из паровой фазы в жидкую, составляет
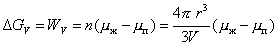 , (2.1.12)
, (2.1.12)
где V – молярный объем вещества в конденсированной фазе.
Работа (или свободная энергия) образования одной частицы при конденсации
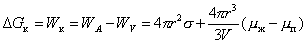 . (2.1.13)
. (2.1.13)
Химический потенциал вещества mr в частице оказывается выше по сравнению с химическим потенциалом mж в конденсированной макрофазе (жидкости):
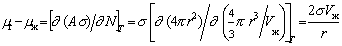 , (2.1.14)
, (2.1.14)
где А – площадь поверхности частицы; N – число молекул, образующих частицу; r – радиус частицы.
При квазиравновесном образовании частиц в результате возникновения критических зародышей новой фазы
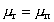 , (2.1.15)
, (2.1.15)
поэтому с учетом (2.1.13)
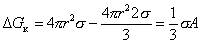 . (2.1.16)
. (2.1.16)
Уравнение (2.1.16), которое впервые было получено Гиббсом, показывает, что работа образования частиц (капель) при неустойчивом равновесии составляет 1/3 работы образования ее поверхности, т.е.
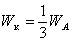 . (2.1.17)
. (2.1.17)
Оставшиеся 2/3 WA компенсируются работой самопроизвольного фазового перехода.
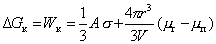 . (2.1.18)
. (2.1.18)
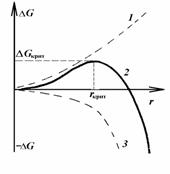
Рис. 2.2. Зависимость изменения энергии Гиббса при образовании капель от их размера |
В уравнении (2.1.18) первый член всегда положителен и растет при увеличении размера частицы (капли) как fr2 (кривая 1 рис. 2.2) Второй член этого уравнения может быть отрицательным, если Dm < 0, но при этом его абсолютная величина растет как fr3 (кривая 3 рис. 2.2). Поэтому на зависимости работы образования единичной частицы от ее размера появляется максимум, как это показано на кривой 2 рис. 2.2. Этот максимум отвечает некоторому критическому размеру зародыша новой фазы. Положение максимума на кривой зависимости DG = f(r) можно определить из условия 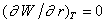 .
.
Дифференцируя уравнение (2.1.13), получаем для критического размера частиц
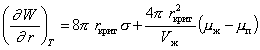 . (2.1.19)
. (2.1.19)
Откуда
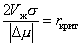 . (2.1.20)
. (2.1.20)
Учитывая полученное ранее уравнение (2.1.10) для изменения химического потенциала при критическом образовании зародышей,

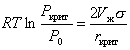 . (2.1.21)
. (2.1.21)
Уравнение (2.1.21) можно записать в форме
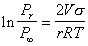 , (2.1.21а)
, (2.1.21а)
где 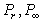 – давление насыщенного пара над выпуклой сферической поверхностью радиуса r и над плоской поверхностью макрофазы (
– давление насыщенного пара над выпуклой сферической поверхностью радиуса r и над плоской поверхностью макрофазы (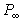 эквивалентно Р0, введенному нами ранее).
эквивалентно Р0, введенному нами ранее).
Это уравнение, известное как уравнение Кельвина (Томсона), было получено еще в 1870 г.
Уравнение (2.1.21) можно записать как
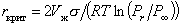 . (2.1.22)
. (2.1.22)
С учетом уравнения (2.1.16) энергия Гиббса образования критического зародыша
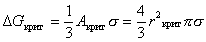 . (2.1.23)
. (2.1.23)
Заменяя rкрит выражением (2.1.22), получаем
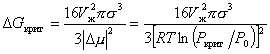 . (2.1.24)
. (2.1.24)
Таким образом, работу образования критического зародыша новой фазы - коллоидных частиц - можно рассматривать как энергетический барьер, который необходимо преодолеть, чтобы дальше процесс роста зародышей шел самопроизвольно. Частицы радиуса r < rкрит могут только исчезать, так как степень пересыщения будет меньше критической и работа образования их поверхности будет расти при увеличении радиуса быстрее, чем будет уменьшаться свободная энергия при конденсации пара в жидкость. Если радиус зародышей достиг критического, то дальнейший их рост приводит к снижению свободной энергии системы в результате того, что снижение свободной энергии при конденсации пара в жидкость компенсирует свободную энергию поверхности. Таким образом,в системе может сформироваться набор частиц различного размера, что препятствует образованию устойчивых коллоидных систем, так как всегда в полидисперсных системах большие капли (частицы) будут расти за счет маленьких капель (частиц).
Вместе с тем, самопроизвольное (гомогенное) образование зародышей новой фазы - коллоидных частиц - возможно только при больших степенях пересыщения. Степень пересыщения, как видно из уравнения (2.1.21), тем выше, чем больше размер частиц (капель).
Конденсацией из газовой (паровой) фазы получают аэрозоли, туманы, дымы, смог. Эти коллоидные системы могут образовываться на всех текстильных предприятиях, а также на заводах по производству химических волокон, если на их территории расположены тепловые электростанции, котлы которых работают на жидком или твердом топливе.