Электронно-колебательное взаимодействие
ЭЛЕКТРОННО-КОЛЕБАТЕЛЬНОЕ ВЗАИМОДЕЙСТВИЕ, составляющая полного взаимод. частиц в молекуле или твердом теле, возникающая в приближении, основанном на разделении электронных движений и колебаний ядер. Электронно-колебательное взаимодействие наз. также вибронным взаимодействием (от англ. vibrational electronic), хотя термин "вибронный" в широком смысле означает все электронно-колебат. (вибронные) квантовые состояния и соответствующие этим состояниям уровни энергии.Разделение переменных, характеризующих электронные и ядерные движения в молекуле, обычно проводится в рамках т. наз. грубого приближения Борна-Оппенгеймера (см. Адиабатическое приближение), в к-ром электронная волновая функция
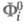 задается лишь для нек-рой фиксир. геом. конфигурации ядер
задается лишь для нек-рой фиксир. геом. конфигурации ядер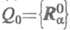 , где
, где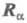 - радиус-вектор ядра a, индекс "0" указывает на то, что рассматривается фиксир. конфигурация, а фигурные скобки - на то, что учитывается все множество независимых радиусов-векторов. В этом приближении потенциал электронно-колебательного взаимодействия определяется выражением:
- радиус-вектор ядра a, индекс "0" указывает на то, что рассматривается фиксир. конфигурация, а фигурные скобки - на то, что учитывается все множество независимых радиусов-векторов. В этом приближении потенциал электронно-колебательного взаимодействия определяется выражением: 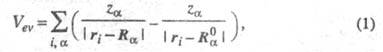
где ri - радиусы-векторы электронов;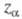 - заряд ядра
- заряд ядра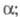
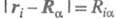 - расстояние от ядра
- расстояние от ядра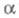 до электрона i; суммирование ведется подиндексам всех электронов и ядер. Любая другая конфигурация, получающаяся в результате малых смещений ядер
до электрона i; суммирование ведется подиндексам всех электронов и ядер. Любая другая конфигурация, получающаяся в результате малых смещений ядер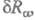 м. б. описана линейнонезависимыми обобщенными координатами qv:
м. б. описана линейнонезависимыми обобщенными координатами qv:
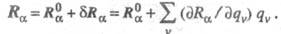
Для такой конфигурации потенциал электронно-колебательное взаимодействия VeV можно записать в виде ряда разложения по степеням qv:
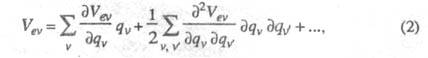
причем все производные взяты в точке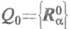 многомерного пространства ядерных конфигураций. Эти производные зависят только от электронных переменных, тогда как колебат. координаты qvсуть малые смещения ядер. Поскольку потенциал Vev содержит произведение тех и других, то он и называется потенциалом электронно-колебательного взаимодействия.
многомерного пространства ядерных конфигураций. Эти производные зависят только от электронных переменных, тогда как колебат. координаты qvсуть малые смещения ядер. Поскольку потенциал Vev содержит произведение тех и других, то он и называется потенциалом электронно-колебательного взаимодействия.
В адиабатич. приближении электронная волновая ф-ция Фi (r, R)зависит от переменных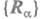 мгновенной ядерной конфигурации (в отсутствие вращения молекулы), поэтому электронно-колебательное взаимодействие задается операторами неадиабатич. связи электронного и колебат. движений. В простейшем случае двухатомной молекулы мгновенная ядерная конфигурация определяется всего лишь одной координатой R = |Rl—R2|, а энергия электронно-колебательного взаимодействия и поправки к волновым ф-циям, обусловленные этим взаимод., зависят от множества величин вида
мгновенной ядерной конфигурации (в отсутствие вращения молекулы), поэтому электронно-колебательное взаимодействие задается операторами неадиабатич. связи электронного и колебат. движений. В простейшем случае двухатомной молекулы мгновенная ядерная конфигурация определяется всего лишь одной координатой R = |Rl—R2|, а энергия электронно-колебательного взаимодействия и поправки к волновым ф-циям, обусловленные этим взаимод., зависят от множества величин вида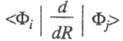 и
и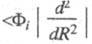 Ф;> (i,j=1, 2, ...; угловые скобки означают интегрирование по электронным переменным), к-рые после преобразований м. б. сведены к выражениям, подобным (1) и (2) для грубого приближения Борна-Оппенгеймера.
Ф;> (i,j=1, 2, ...; угловые скобки означают интегрирование по электронным переменным), к-рые после преобразований м. б. сведены к выражениям, подобным (1) и (2) для грубого приближения Борна-Оппенгеймера.
Как правило, электронно-колебательное взаимодействие проявляется особенно сильно тогда, когда в молекуле имеются два близко расположенные квантовые состояния одного и того же типа симметрии, напр. состояния 1 и 2 с волновыми ф-циями соотв.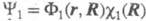 и
и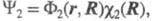 где
где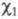 и
и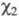 - волновые ф-ции для ядерной подсистемы в отсутствие электронно-колебательного взаимодействия. В силу того, что адиабатич. представление волновых ф-ций приближенно, более точное описание этих квантовых состояний имеет вид:
- волновые ф-ции для ядерной подсистемы в отсутствие электронно-колебательного взаимодействия. В силу того, что адиабатич. представление волновых ф-ций приближенно, более точное описание этих квантовых состояний имеет вид:
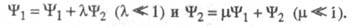
Обычно эта ситуация передается такими словами: "в состоянии 1 к ф-ции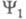 примешана ф-ция
примешана ф-ция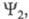 а в состоянии 2 к ф-ции
а в состоянии 2 к ф-ции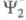 примешана ф-ция
примешана ф-ция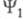 ". Следует отметить, что связанные с электронно-колебательным взаимодействием энергетич. поправки к адиабатич. приближению гораздо меньше, чем таковые к грубому приближению Борна-Оппенгеймера.
". Следует отметить, что связанные с электронно-колебательным взаимодействием энергетич. поправки к адиабатич. приближению гораздо меньше, чем таковые к грубому приближению Борна-Оппенгеймера.
Учет электронно-колебательного взаимодействия приводит к ряду весьма важных эффектов. Для высокосимметричных молекул электронно-колебательное взаимодействие обусловливает появление Яна - Теллера эффектов, в частности расщепление уровней высокосимметричной конфигурации при понижении ее симметрии. Для молекул с более низкой симметрией оно изменяет правила отбора в мол. спектрах и приводит к перераспределению интенсивности линий и полос в этих спектрах. Так, правила отбора уже нельзя сформулировать отдельно для электронных и колебат. переходов, они будут определяться полными электронно-колебат. волновыми ф-циями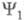 и
и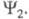 В частности, если переход между возбужденным 1
В частности, если переход между возбужденным 1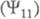 и основным 0
и основным 0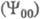 состояниями в адиабатич. приближении был запрещен, а переход между возбужденным 2
состояниями в адиабатич. приближении был запрещен, а переход между возбужденным 2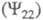 и основным состояниями разрешен, то при учете электронно-колебательного взаимодействия волновая ф-ция
и основным состояниями разрешен, то при учете электронно-колебательного взаимодействия волновая ф-ция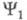 первого возбужденного состояния 1 в общем случае будет содержать примесь ф-ции
первого возбужденного состояния 1 в общем случае будет содержать примесь ф-ции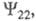 и переход, становится разрешенным. В этом случае говорят о "заимствовании интенсивности" переходом 0
и переход, становится разрешенным. В этом случае говорят о "заимствовании интенсивности" переходом 0 1 у перехода 0
1 у перехода 0 2.
2.
При возбуждении молекулы связанное электронно-колебат. состояние, в к-рое она переходит, по энергии м. б. очень близко к отталкивательному электронно-колебат. состоянию. За счет электронно-колебательного взаимодействия происходит безызлучательный переход в отталкиват. состояние, что приводит к диссоциации молекулы (см. Предиссоциация).
Электронно-колебательное взаимодействие определяет неадиабатич. характер многих хим. р-ций, для к-рых описание поведения реагирующей системы невозможно в рамках представления о движении точки, изображающей эту систему, по единственной потенц. пов-сти (см. Динамика элементарного акта). Области вблизи барьера на пути р-ции по пов-сти потенц. энергии отвечают, как правило, сближению потенц. пов-стей (одной и той же симметрии) и перестройке электронной конфигурации системы. В этих областях учет электронно-колебательного взаимодействия становится, по-существу, обязательным. В ходе р-ции система взаимодействующих атомов и молекул проходит хотя бы через одну такую область, где адиабатич. приближение перестает быть справедливым и его необходимо.заменять на приближения, лучше учитывающие электронно-колебательное взаимодействие (наряду с др. эффектами, напр., спин-орбитальным взаимодействием).
Лит.: Берсукер И. Б., Полингер В. 3., Вибронные взаимодействия в молекулах и кристаллах, М., 1983; Жилинский Б.М., Теория сложных молекулярных спектров, М., 1989.
Я. Ф. Степанов.
