Спин-орбитальное взаимодействие

СПИН-ОРБИТАЛЬНОЕ ВЗАИМОДЕЙСТВИЕ, взаимодействие между магн. моментами, связанными со спиновыми и орбитальными моментами кол-ва движения электронов и ядер в квантовой системе - атоме, молекуле, кристалле и т.п. Спин-орбитальное взаимодействие обусловливает вклад в энергию системы, к-рому отвечают три слагаемых гамильтониана в ур-нии Шрёдингера. Первое слагаемое связано с магн. полем, возникающим при перемещении электрона относительно ядра в электрич. поле ядра и действующим на спиновый магн. момент; второе-с магн. полем, возникающим при движении данного электрона в электрич. поле всех остальных электронов, третье-с взаимод. спинового магн. момента данного электрона с магн. полями, создаваемыми всеми остальными электронами при их движении.

Для электронов i и j с радиусами-векторами r_i и r_j и импульсами (Моментами кол-ва движения) p_i и p_j их спин-орбитальные взаимодействия друг с другом и с ядрами а, заряды к-рых равны Z_a (в единицах элементарного заряда е) и радиусы-векторы R_a, приводит к дополнит. вкладу в гамильтониан системы, состоящему из след. трех сумм:

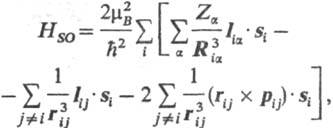
где ђ и m_В-постоянная Планка и магнетон Бора соотв.; R_ia = r_i-R_a, r_ij=r_i — r_j (r_ij-длина вектора r_ij); I_ia = = (r_i — R_a)x p_i - момент кол-ва движения i-го электрона относительно начала системы координат на ядре a, р_ij = =p_i - p_j, I_ij = r_ij x p_i, s_i-оператор спина i-го электрона.

Из этих сумм, как правило, осн. вклад в энергию системы дает первая, тогда как вторая и третья (их обычно наз. "взаимодействия спин-другая орбиталь") дают значительно меньшие вклады. Если ими пренебречь, оператор спин-орбитального взаимодействия сводится к следующему:

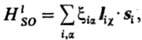
где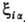- ф-ции координат электронов и ядер, а также зарядов ядер. Эти ф-ции пропорциональны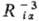, поэтому при их усреднении по всем возможным положениям электронов наиб. существенны те конфигурации системы, при к-рых электроны находятся вблизи ядер. Если волновая ф-ция молекулы образована из мол. орбиталей в форме линейной комбинации атомных орбиталей (см. ЛКАО-приближение), то в средние величины 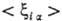основной вклад дают интегралы 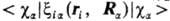, вычисляемые с атомными орбиталями c_a, центрированными на ядре a (см. Орбиталь). Обычно ф-ции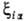(r_i, R_a) для атомов заменяют на нек-рые постоянные, зависящие от главного n и орбитального l квантовых чисел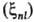; их наз. постоянными спин-орбитальными взаимодействиями. В водородоподобных атомах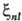пропорциональна Z⁴ и обратно пропорциональна n³. В многоэлектронных атомах происходит экранирование ядра электронами и зависимость постоянной спин-орбитального взаимодействия от Z и n становится не столь резко выраженной и функционально более сложной. Тем не менее и в том и в другом случае спин-орбитальное взаимодействие наиб. велико для электронов внутр. оболочек тяжелых атомов, а у молекул-для внутр. оболочек атомных остовов, что позволяет характеризовать величины спин-орбитальнох взаимодействий и для молекул с помощью атомных постоянных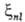

Спин-орбитальное взаимодействие приводит к расщеплению вырожденных уровней мультиплета, что проявляется в атомных и мол. спектрах как тонкая структура. Так, вследствие спин-орбитального взаимодействия низший возбужденный уровень атомов щелочных металлов расщепляется на два: ²P_1/2 и ²Р_3/2, где индекс внизу указывает квантовое число полного момента кол-ва движения электрона на внеш. оболочке пр. Для Na (Z = 11, n = 3) это расщепление составляет 17,2см^-1, для К (Z=19, n = 4) 57,7 см ^-1, для Cs (Z =55, n = 6) 554,1 см ^-1. У атомов галогенов расщепление уровней для np-электронов еще больше, а постоянные спин-орбитального взаимодействия таковы: для F 272 см ^-1, для Сl 587 см ^-1, для I 5060 см ^-1. При достаточно сильном спин-орбитальном взаимодействии понятие мультиплетности термов вообще теряет смысл и рассматривается лишь полный момент кол-ва движения электронов, а не спин и орбитальный момент в отдельности. Запрет на квантовые переходы между уровнями с разной мультиплетностью при наличии спин-орбитального взаимодействия снимается, что приводит, напр., к фосфоресценции - излучат. переходу из состояний с временами жизни, обратно пропорциональными квадратам матричных элементов оператора спин-орбитального взаимодействия, и к ин-теркомбинац. конверсии (см. Люминесценция, Фотохимические реакции). Поскольку время фосфоресценции зависит не только непосредственно от времени жизни "фосфоресцирующего" состояния рассматриваемых молекул, но и от среды, в к-рой они находятся, для учета этой зависимости вводят представление о межмолекулярном спин-орбитальном взаимодействии. У двухатомных и линейных многоатомных молекул соотношение спин-орбитального взаимодействия и др. взаимодействий, напр. спин-вращательного, позволяет выделять разл. случаи связи спинов, орбитальных и др. моментов (см. Хунда случаи связи), что дает возможность для каждого случая связи проводить специфич. классификацию квантовых состояний молекулы.

В выражении для H_SO не представлен член, отвечающий взаимод. ядерного магн. спинового момента и орбитального момента электронов, 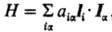, где а_ia(R_ia) =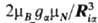, g_a-g-фактор ядра a, m_N- ядерный магнетон, I_a- ядерный спин. Связанное с этим членом расщепление уровней заметно меньше, чем обусловленное спин-орбитальное взаимодействие; напр., для электронного состояния ²Р_1/2 атома Na величина a_ia составляет 94,5 МГц, а для состояния ²Р_3/2-19,1 МГц, т.е. примерно 0,003-0,001 см^-1. Обычно член Я выделяют (вместе с др. членами того же порядка малости) в орбитальное сверхтонкое взаимодействие, или сверхтонкое ядерное магн. взаимодействие, проявляющееся в спектрах ЭПР (см. Электронный парамагнитный резонанс).

Лит. см. при ст. Спин. Н. В. Степанов.

• СПИН-СПИНОВОЕ ВЗАИМОДЕЙСТВИЕ - химическая энциклопедия