4.1.2. Вязкость разбавленных дисперсных систем
Если в разбавленных дисперсных системах (при отсутствии взаимодействия между диспергированными частицами) размер частиц оказывается значительно большим, чем размер молекул жидкости, но намного меньшим, чем радиус капилляров, по которым такая жидкость течет, то макроскопическая вязкость, измеренная каким-либо методом, будет отличаться от вязкости чистой жидкости, хотя течение такой системы может быть описано законом Ньютона. Происходит это потому, что частица, по своим размерам намного превосходящая молекулы жидкости, искажает картину течения слоев жидкости.
Для сферических частиц расчет вязкого сопротивления потока жидкости, в котором находятся сферические частицы, был проведен Стоксом.
Для несжимаемых гладких сферических частиц, движущихся вдали от стенок капилляра так, что плоскость разрыва между частицей и жидкой фазой проходит в жидкости, сила, уравновешивающая силу потока на неподвижную частицу, составит
F = BU0 = 6phrU0, (2.4.13)
где r – радиус частиц, U0 – скорость движения частицы относительно жидкости, h – вязкость жидкости.
Сила трения и коэффициент вязкого сопротивления движению асимметричных частиц зависит от ориентации таких частиц в потоке жидкости. Существует ряд уравнений для расчета коэффициента трения В для частиц различной формы.
Влияние частиц дисперсной фазы на вязкое течение жидкостей будет состоять в том, что те слои, которые прилегают непосредственно к частицам, могут перемещаться только с той же скоростью, что и частицы. Этот эффект был рассчитан Эйнштейном (1906 г.) для сферических частиц. Принимая, что на достаточном удалении от поверхности частицы поток имеет постоянную скорость, а сама частица перемещается вместе с потоком, Эйнштейн получил уравнение для вязкости дисперсной системы
h= h0( 1+2,5j ) , (2.4.14)
или
h/h0 = hотн = 1 + 2,5j , (2.4.15)
где h – вязкость дисперсной среды; j – объемная доля частиц дисперсной фазы; 2,5 – коэффициент формы сферических частиц; hотн= h/h0– относительная вязкость.
Симха распространил метод Эйнштейна на дисперсии с частицами, имеющими форму, отличающуюся от сферической при низких градиентах скорости течения, когда частицы ориентированы длинной осью параллельно течению, получил уравнение
h= h0(1 +uj), (2.4.16)
гдеu – коэффициент формы частиц; для асимметричных частиц всегда больше 2,5.
При больших градиентах скорости течения частицы могут располагаться беспорядочно, в том числе и поперек течения, что приводит к образованию локальных турбулентных областей, для таких дисперсий характерно неньютоновское течение.
Уравнение (2.4.16), известное как уравнение Симха-Эйштейна, общее как для сферических, так и для несферических частиц, часто записывают в форме
hуд = (h-h0)/h0 = uj , (2.4.17)
где hуд– удельная вязкость – безразмерная величина, показывающая приращение вязкости относительно вязкости дисперсионной среды, приходящееся на дисперсную фазу.
Можно отметить, что удельная вязкость зависит только от общего объема, занятого дисперсной фазой и не зависит от размера частиц и их распределения по размерам.
Для разбавленных эмульсий, в которых сферические капли жидкости имеют вязкость h', Тейлор получил уравнение
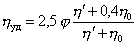. (2.4.18)
Для дисперсных систем, где возможно парное взаимодействие частиц, приводящее к образованию ориентированных вдоль потока временных агрегатов частиц, Симха предложил уравнение, описывающее вязкость систем со сферическими частицами, в котором взаимодействие между частицами и возможные их столкновения при течении дисперсии учитываются дополнительным членом:
hуд = 2,5j + 12,6j2. (2.4.19)
Более точным считается теоретическое уравнение Ванда, полученное для дисперсий, в которых образуются агрегаты из двух частиц. В нем не учитывается рассеивание энергии, возможное при столкновении частиц в потоке,
hуд = 2,5j + 7,34j2. (2.4.20)
Это уравнение нашло экспериментальное подтверждение при изучении поведения стеклянных сфер в водно-глицериновой среде с высокой вязкостью. В водной среде был найден коэффициент для второго члена уравнения (2.4.19), равный от 9 до 13, что согласуется как с уравнением Ванда, так и с уравнением Симха.
В общем виде можно записать уравнение зависимости вязкости дисперсии от объемной концентрации дисперсной фазы в виде
h/h0=1 + aj + bj2 + cj3 +...
или
hуд=aj + bj2 + cj3 +..., (2.4.21)
где h/h0 = hотн – относительная вязкость дисперсной системы.
Это уравнение позволяет учесть все виды взаимодействий, возникающих при течении дисперсных систем. Можно отметить, что при концентрации дисперсной фазы менее 1% при расчете второго члена уравнения (2.4.21) относительная вязкость даже при наибольшем значении постоянной b вносит поправку не более 0,1% от найденной относительной вязкости, что находится в пределах экспериментальной погрешности. Естественно, что при более высокой концентрации дисперсной фазы необходимо учитывать второй член уравнения, а при необходимости высокой точности определения вязкости дисперсий - и третий.
Уравнение (2.4.21) можно использовать и для расчета вязкости несферических частиц в зависимости от концентрации.
Для таких систем уравнение зависимости вязкости от концентрации принимает вид
h/h0= 1 + K1aj + K2a2j2 + K3a3j3 +...+, (2.4.22)
где а – параметр, зависящий от формы частиц; K1, K2, K3,... – безразмерные постоянные.
Постоянная а рассчитывается как отношение длинной оси несферических частиц к короткой.
Постоянные уравнений (2.4.21) и (2.4.22) зависят не только от формы частиц, но и от градиента скорости течения, так как при низких скоростях течения броуновское движение частиц создает большое сопротивление течению, особенно если асимметричные частицы ориентируются поперек потока. В этой связи экспериментально найденная вязкость дисперсных систем с постоянной концентрацией уменьшается при повышении скорости сдвига даже в том случае, если в дисперсии не образуется пространственная структура. Приведенные выше уравнения справедливы для дисперсных систем, в которых на поверхности частиц не образуется двойной электрический слой или в которых не развита его диффузионная часть.
Если же на поверхности частиц образуется двойной ионный слой диффузионной структуры, то в процессе течения диффузионная обкладка может отрываться от частиц, в результате чего частицы приобретают нескомпенсированный заряд и течение может тормозиться в результате электростатического взаимодействия. Этот эффект, называемый электровязкостным, учитывается добавочным членом в уравнении Эйнштейна (2.4.14)
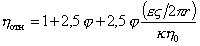, (2.4.23)
где e – диэлектрическая проницаемость среды; z – электрокинетический потенциал; r – радиус частиц; k – удельная электрическая проводимость среды; h0 – вязкость дисперсионной среды.
Уравнение (2.4.23) в 1916 г. предложил Смолуховский для жестких не набухающих частиц. При развитых диффузионных слоях для частиц с r» 10-8 м при k» 10-4 Ом-1×cм-1 поправочный член может быть на порядок больше основного.
При введении электролитов и следующим за этим сжатием двойного ионного слоя вязкость падает до некоторого предельного значения, не зависящего от вида добавленного электролита.
Экспериментальная проверка уравнения (2.4.23) показала, что найденные экспериментальные значения вязкости в 100 раз меньше рассчитанного по уравнению Смолуховского. В связи с этим были предложены другие уравнения, учитывающие электровязкостный эффект, в частности, известное уравнение Буфа:
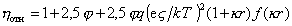, (2.4.24)
где q – постоянная, зависящая от температуры и природы электролита; е – элементарный заряд; k – параметр Дебая, характеризующий толщину двойного ионного слоя; f(kr) – параметр, зависящий от размера частиц и толщины двойного ионного слоя.
Уравнение Буфа более точно учитывает электровязкостный эффект и теоретически предсказывает порядок величины вязкости. Рассчитанные по этому уравнению и найденные экспериментально значения вязкости имеют один порядок, но различаются по величине в 2-3 раза.