4.1.3. Вязкость растворов полимеров

В отличие от коллоидных частиц, форма которых обусловлена способом получения и не изменяется в зависимости от температуры и концентрации дисперсной фазы, форма макромолекул зависит от многих факторов интенсивности межмолекулярного взаимодействия полимерных молекул с растворителем, зависящей от температуры, концентрации полимера в растворе, внутримолекулярных взаимодействий и т.д.

Непосредственно перенести уравнения, полученные для дисперсных систем, на растворы полимеров можно только при соблюдении некоторых условий. В частности, уравнения, описывающие вязкость дисперсных систем, были получены при рассмотрении изменений потока жидкости около индивидуальной частицы, поэтому их можно применять только к разбавленным растворам полимеров, в которых не образуются ассоциаты макромолекул, или экстраполировать измеренные значения вязкости к нулевой концентрации. В этой связи при изучении растворов полимеров часто оперируют с величиной h_уд/с = h_s, называемой приведенной вязкостью:

lim[h_уд/c]_c-o = [h ], (2.4.25)

где[h] – называют характеристической вязкостью.

Чаще всего рассматривают макромолекулу полимера как жесткую частицу, т.е. предполагают, что внутренние связи в макромолекуле не допускают перемещения отдельных ее частей при течении раствора. Естественно, что макромолекулы могут иметь в растворах самую разнообразную форму: сферы, эллипсоида, стержня и т.п. В растворах часть молекул растворителя прочно связана с макромолекулами и перемещается с ними как единая кинетическая единица.

Для характеристики сольватации макромолекул часто используется величина, выраженная в единицах массы связанного растворителя на единицу массы растворенного вещества, называемая числом сольватации и обозначаемая как W_s. В частном случае, когда в качестве растворителя используется вода, эта характеристика называется числом гидратации, или удельной гидратацией и обозначается как W_h.

При течении раствора полимера свернутые в клубки макромолекулы перемещаются совместно с некоторым количеством растворителя, связанным с макромолекулой силами межмолекулярного взаимодействия. В связи с этим при использовании методов, основанных на явлениях переноса, обычно получают молекулярную массу полимера, отличающуюся от ее истинного значения на массу связанного растворителя. Ее следует учитывать при расчете массы гидродинамической частицы, каковой является молекула полимера в текущем растворе. При таком учете масса одной сольватированной молекулы

m_s = M(1 + W_s) / N. (2.4.26)

Экспериментальное определение числа сольватации W_s обычно представляет собой сложную задачу, так как различные методы позволяют найти лишь ту или иную часть растворителя, связанного с растворенным веществом. Один из наиболее распространенных методов изучения гидратации – вискозиметрия.

При расчетах сольватации из вискозиметрических данных объемную долю растворенного вещества заменяют концентрацией растворенных молекул

j₂ = v_efC,

где j₂– объемная доля растворенного вещества; C– концентрация, г/см³, раствора; v_ef – эффективный объем макромолекул в растворе, совместно с объемом связанного растворителя.

Если выделить некоторый объем V раствора, то он будет состоять из объема, занятого макромолекулами g₂v₂, объема, занятого связанным растворителем g₂W_sv₁, и объема, занятого свободным растворителем (g₁– g₂W_s)v₁⁰:

V = g₂v₂, + g₂W_sv₁ +(g₁– g₂W_s)v₁⁰, (2.4.27)

где v₂ – удельный объем сухого растворенного полимера; v₁, v₁⁰– удельный объем связанного и свободного растворителя; g₂ – масса растворенного вещества.

Для очень разбавленных растворов, когда W_s уже не зависит от концентрации, можно перейти от объема раствора к парциальному удельному объему 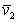растворенного вещества дифференцированием уравнения (2.4.27) по массе растворенного полимера:

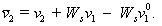(2.4.28)

Объем одной сольватированной макромолекулы в растворе

v_s = M(v₂ + W_sv₁) / N , (2.4.29)

или с учетом (2.4.28)

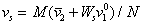. (2.4.30)

Обычно парциальный удельный объем растворенного вещества находят методом измерения плотности раствора при изменении его концентрации, удельный объем растворителя – как v₁=1/r₁, объем сольватированной частицы находят по измеренной вязкости, а молекулярную массу полимера измеряют каким-либо независимым методом. После этого можно рассчитать W_s . Для нахождения числа гидратации определяют характеристическую вязкость, записывая уравнение (2.4.21) в форме

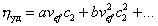(2.4.31)

или

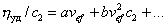(2.4.32)

и вводя обозначение аv_ef =[h]:

h_уд/c₂ = [h]+K' [h]²c₂. (2.4.33)

Уравнение (2.4.33) называют уравнением Хаггинса, где K'– постоянная Хаггинса, для сферических макромолекул, близкая к 2,0.

Таким образом, после экстраполяции к нулевой концентрации находят характеристическую вязкость [h], размерность которой см³/г, и затем рассчитывают сольватацию. Так как

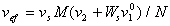, (2.4.34)

поэтому

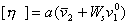, (2.4.35)

где а = 2,5 для сферических макромолекул.

Если форма макромолекул в растворах сильно отклоняется от сферической, что можно определить по постоянной Хаггинса, то коэффициент формы находят независимым методом, например, по рассеянию света в растворах полимера под различным углом к падающему свету, и только после этого определяют сольватацию.

Существует ряд эмпирических и полуэмпирических формул, которые связывают характеристическую вязкость с молекулярной массой растворенного полимера. На основе этого существует необычайно простой метод определения молекулярной массы полимера по вязкости его разбавленных растворов, требующий предварительной калибровки постоянных расчетного уравнения по значениям молекулярной массы, измеренной предварительно каким-либо независимым методом.

Эмпирическое уравнение, впервые предложенное Марком и Хаувинком (1940 г.), связывающее молекулярную массу и характеристическую вязкость, имеет вид

[h ] = KM ^a, (2.4.36)

где K и а – постоянные, зависящие от природы полимера, растворителя и температуры. Постоянная а для гибких макромолекул изменяется в небольших пределах (от 0,5 до 0,8). Жесткие стержнеобразные молекулы имеют а = 1,8.

Молекулярная масса, определяемая вискозиметрическим методом, может быть как среднечисленной, так и среднемассовой, в зависимости от того, каким методом определена молекулярная масса полимера при калибровке постоянных K и а. Более того, если использовать различные методы предварительного определения молекулярной массы, то и постоянные для одного и того же полимера будут различными даже при одной температуре.