2.2. Седиментационный анализ
2.2.1. Основы теории седиментации

Седиментационный анализ - один из наиболее широко применяемых непрямых методов определения размера частиц и их распределения по размерам. Седиментационный анализ основан на зависимости скорости осаждения однородных частиц от их размеров. Грубодисперсные системы изучают методом седиментации в гравитационном поле, а тонкодисперсные и коллоидно-дисперсные - методом седиментации в центрифуге и в ультрацентрифуге.

В вязкой и плотной среде при седиментации частица движется под действием силы тяжести в гравитационном поле. Сила сопротивления среды, действующая на сферическую частицу, зависит от ее размера, скорости движения, вязкости среды и характеризуется числом Рейнольдса

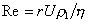, (2.2.9)

где r – радиус частиц; U – скорость движения; r₁,h – плотность и вязкость среды.

Коэффициент сопротивления среды движущейся частицы

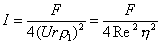, (2.2.10)

где F – сила сопротивления среды.

В соответствии с законом Стокса

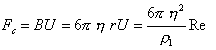. (2.2.11)

Гидродинамическое сопротивление среды описывается законом Ньютона-Риттера

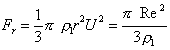. (2.2.12)

Сопротивление среды определяется суммой сил по уравнениям (2.2.11) и (2.2.12):

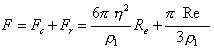. (2.2.13)

В области чисел Рейнольдса (Re<<1) можно пренебречь вторым слагаемым уравнения (2.2.13), а при (Re>>1) – первым.

В промежуточном случае можно использовать уравнение Озеена:

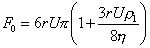. (2.2.14)

Закон Стокса справедлив в области Re<<0,2. Поправка Озеена существенна в области чисел от 0,2 до 10, а закон Ньютона-Риттера описывает движение частиц в области чисел Рейнольдса от 10² до 10⁵.

Если размер частиц и скорость их осаждения невелики, то для описания силы сопротивления среды можно использовать закон Стокса.

Сила тяжести, действующая на частицу, равна кажущейся массе,

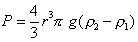, (2.2.15)

где g – ускорение свободного падения.

Движение частиц будет направлено вниз, если разность плотностей дисперсной фазы r₂ и дисперсионной среды r₁ (Dr) положительна, и частицы будут всплывать при Dr<0.

Под действием силы Р частицы приходят в равномерно ускоренное движение. Но так как, кроме силы тяжести, на них действует сила сопротивления среды, направленная противоположно и возрастающая пропорционально скорости, то очень скоро сила сопротивления среды уравновешивает силу тяжести, благодаря этому далее движение идет равномерно со скоростью U.

Если экспериментально определить скорость седиментации, то можно рассчитать радиус частиц; так как при стационарном режиме осаждения F = P.

Поэтому

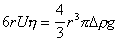, (2.2.16)

откуда

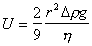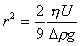или , (2.2.17)

следовательно

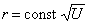. (2.2.18)

Уравнение Стокса (2.2.17) было выведено при соблюдении ряда условий, которые не всегда соблюдаются в реальных системах:

1. Частицы должны быть сферическими. Это условие обычно выполняется для разбавленных эмульсий и частиц полимеров, полученных методом эмульсионной полимеризации. Частицы суспензий часто отклоняются от сферической формы, поэтому для них определяется некоторый эффективный радиус частицы той же массы, движущейся с той же скоростью. Такой радиус называют эквивалентным или эффективным.

2. Отсутствие взаимодействия между частицами. Расстояние между частицами должно быть достаточно большим, чтобы падение одних частиц не сказывалось на скорости других. Поэтому анализ следует проводить при невысоких концентрациях (1-2%).

3. Необходимо, чтобы сосуд, в котором происходит седиментация, был намного больше размеров частиц. Это необходимо для того, чтобы можно было пренебречь влиянием стенок, так как вблизи стенок скорость оседания не следует закону Стокса.

4. Движущиеся частицы должны быть твердыми и гладкими. Это условие связано с возможностью изменения формы частиц в результате возникновения в них микропотоков. Условие не выполняется при течении эмульсий.

5. Отсутствие проскальзывания между оседающей частицей и средой. Необходимо, чтобы частица хорошо смачивалась жидкостью, так как в уравнение (2.2.17) входит h – вязкость именно жидкости.

6. Скорость оседания должна быть постоянной, иначе сила тяжести не уравновесится силой трения.

7. Скорость оседания должна быть небольшой, в противном случае возникает турбулентный режим течения, и тогда нельзя будет использовать вязкость h, соответствующую ламинарному режиму течения.

• СЕДИМЕНТАЦИОННЫЙ АНАЛИЗ - химическая энциклопедия