2.2.4. Седиментация в центрифуге
В 1910 г. А.В. Думанский предложил ускорить осаждение частиц суспензий, используя центрифугу. В 1923 г. Т. Сведберг сконструировал первую ультрацентрифугу. В течение ряда лет конструкция ультрацентрифуг совершенствовалась. Первоначальное ускорение 5 тыс. g было доведено до 900 тыс. g. Но такое ускорение оказалось избыточным, так как впоследствии оказалось, что для исследовательских целей достаточно ультрацентрифуги с ускорением 40-50 тыс. g.
Если поле земного тяготения заменить центробежным полем, то можно значительно ускорить осаждение частиц. При этом можно разделить системы, содержащие частицы, вплоть до коллоидных размеров и даже осаждать молекулы ВМС. Скорость осаждения зависит от интенсивности центробежного поля, а степень осаждения - от времени центрифугирования.
Для характеристики центрифуг применяется величина, называемая фактором разделения
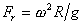, (2.2.55)
где w = pn / 30 – угловая скорость ротора, с-1; n – частота вращения ротора, мин-1; R – внутренний радиус ротора центрифуги; g – ускорение силы тяжести, м/с2.
Она показывает, во сколько раз ускорение центробежного поля больше ускорения силы свободного падения.
Для приближенного расчета скорости осаждения в центробежном поле можно воспользоваться уравнением Стокса, если вместо ускорения свободного падения g подставить ускорение в центробежном поле w2R:
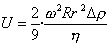, (2.2.56)
или
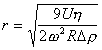. (2.2.57)
Заменяя w2R на Frg, где Fr– фактор разделения центрифуги, получаем
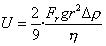, (2.2.58)
или
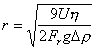. (2.2.59)
Задаваясь фактором разделения центрифуги, а также зная размер частиц, вязкость среды и разность плотностей дисперсной фазы и дисперсионной среды, можно определить скорость осаждения, или время центрифугирования, что особенно важно для осветления воды при ее очистке:
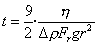. (2.2.60)
Для точных расчетов необходимо учитывать, что ускорение, действующее на частицу в центробежном поле, увеличивается по мере оседания частиц, т.е. удаления их от оси вращения ротора. Поэтому уравнение Стокса следует выражать в дифференциальном виде:
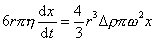, (2.2.61)
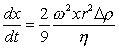, (2.2.62)
где x – расстояние от частицы до оси вращения.
После интегрирования в пределах от x0 (начальное расстояние от частицы до оси вращения) до x (конечное расстояние, т.е. внутренний радиус ротора центрифуги) и соответственно от 0 до t, получаем
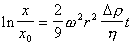, (2.2.63)
откуда
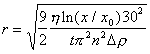, (2.2.64)
где t – время центрифугирования, с.; h – вязкость среды, Па; Dr – разность плотностей дисперсной фазы и дисперсионной среды (кг/м3); n – частота вращения ротора центрифуги, мин-1; x = R – внутренний радиус ротора центрифуги, м; x0 – расстояние от оси вращения до поверхности жидкости в роторе, м.