2.2.3. Кинетические кривые накопления осадка и их обработка
На рис. 2.10 показаны кинетические кривые осаждения частиц (накопления осадка). Масса осадка монодисперсной суспензии Q (см. рис.2.10, а) пропорциональна времени осаждения t, поэтому скорость осаждения
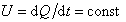 . (2.2.23)
. (2.2.23)
После выпадения всех частиц количество осадка остается неизменным (участок кинетической кривой, параллельный оси абсцисс).
У бидисперсной суспензии (рис. 2.10, б) кинетическая кривая состоит из трех линейных участков. На участке 0А' выпадают частицы одновременно двух фракций. Для того чтобы определить скорость оседания частиц каждой фракции, продолжаем участок А'В' до пересечения с осью Q; получаем отрезок 0y, равный полной массе фракции I (100 %), отрезок yx соответствует массе фракции II (100%). Линия 0В, параллельная yВ', соответствует осаждению фракции II. Скорость осаждения фракции I определяется по наклону прямой 0А, которая проводится из начала координат до точки А, находящейся на пересечении перпендикуляра к оси абсцисс из точки А' и линии, параллельной оси абсцисс, исходящей из точки y. Скорость осаждения частиц каждой фракции определяется как
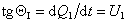 ; (2.2.24)
; (2.2.24)
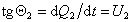 . (2.2.25)
. (2.2.25)
На рис. 2.10, б показана масса каждой фракции и всего осадка как: I – 100% 1-й фракции; II – 100% 2-й фракции; III – 100% осадка.
Кинетическая кривая накопления осадка полидисперсной суспензии представляет собой бесконечно ломаную линию, в пределе переходящую в плавную кривую. Пример такой зависимости представлен на рис. 2.11.
На участке 0 – tm
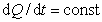 . (2.2.26)
. (2.2.26)
Рис. 2.11. Кинетическая кривая седиментации полидисперсной суспензии |
Пока не выпала полностью первая фракция, в суспензии присутствуют частицы всех размеров. После того как t станет больше tm
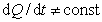 . (2.2.27)
. (2.2.27)
В этом случае количество вещества, выпавшего из суспензии, описывается уравнением касательной
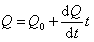 . (2.2.28)
. (2.2.28)
Например, для времени t1Q = 0Q1- ордината точки М1.
Произведению  соответствует отрезок L1Q1
соответствует отрезок L1Q1
Так как
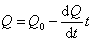 , (2.2.29)
, (2.2.29)
то
Q0= 0L1. (2.2.30)
По углу наклона касательной М1L1 – определяют
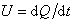 (2.2.31)
(2.2.31)
и рассчитывают r1ср.
Таким образом обрабатывается вся кривая для ряда точек, и определяются соответственно r1 , r2 , r3 и т.д.
Полученные результаты используют для построения интегральной кривой распределения в координатах 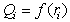 .
.
Наиболее наглядно выглядит кривая распределения в дифференциальном виде. Площадь между кривой и осью абсцисс дает общее число частиц всех размеров, т.е. 100% осадка
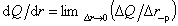 . (2.2.32)
. (2.2.32)
Метод графического дифференцирования недостаточно точен, поэтому в тех случаях, когда необходима высокая точность результатов, используют аналитический метод, предложенный Н.Н. Цюрупой.
После анализа огромного экспериментального материала по обработке кинетических кривых седиментации Н.Н. Цюрупа нашел простой и эффективный способ, с помощью которого можно легко перейти от кинетической кривой седиментации к кривой распределения частиц в суспензии по размерам. Путем многочисленных наблюдений было установлено, что независимо от используемой экспериментальной техники седиментационного анализа, кривая накопления осадка полидисперсной суспензии описывается уравнением
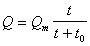 , (2.2.33)
, (2.2.33)
где Q – количество осадка, выпавшего к моменту времени t (% по массе); Qm – постоянная, значения которой лежат в пределах от 100 до 145%; t0 – время осаждения половины осадка, так как при t = t0 из уравнения (2.2.33) следует, что Q = Qm/2.
Рассмотрим кинетическую кривую седиментации, показанную на рис. 2.11. В начальный период осаждения на этой кривой имеется линейный участок 0В, так как в начальный момент времени равномерно оседают частицы всех размеров. С того момента, когда осядут самые крупные частицы (точка В, tm) скорость накопления осадка уменьшится и кинетическая зависимость не будет линейной.
По величине tm рассчитывают rmax – радиус самых крупных частиц.
Общая масса дисперсной фазы, осевшей к любому моменту времени tх
Q = Q0 + q, (2.2.34)
где Q0, q – доли (% по массе) полностью выпавшей фракции и фракции, которая выпала частично ко времени tx лишь из нижних слоев суспензии.
Скорость оседания этой фракции можно выразить как dQ/dt при tx, поэтому доля частично выпавших частиц q к моменту времени tx будет (dQ/dt)tx.
Для полного количества осадка можно записать
Q = Q0 + (dQ/dt)tx. (2.2.35)
Это уравнение представляет собой уравнение касательной, проведенной в точке М1 к кинетической кривой седиментации; Q0 находим как отрезок 0L1 на оси ординат (он соответствует доле фракции частиц с радиусом rx, полностью выпавшей к заданному времени tx).
Аналогичные рассуждения справедливы для касательных, проведенных к любой точке кривой седиментации в любой произвольный момент времени.
Пользуясь уравнением Стокса для седиментации в гравитационном поле (2.2.17) легко подсчитать для любого момента времени ti размер полностью выпавших частиц. Каждая точка на кривой соответствует доле (%) в общей массе полностью осевших к заданному времени той фракции, частицы которой имеют радиус ri и больше ri.
Для построения интегральной и дифференциальной кривых распределения частиц по размерам обычно используют метод построения касательных к кинетической кривой. Максимальный радиус rmax находят после определения времени полного выпадения первой фракции tm. Расчет проводят по уравнению Стокса. Для расчета rmin необходимо рассчитать время полного осаждения частиц tк в суспензии, которое трудно определить экспериментально. Для того, чтобы избежать этого, используют уравнение
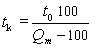 . (2.2.36)
. (2.2.36)
Значения Qm и t0 находят по линейной форме уравнения
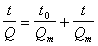 . (2.2.37)
. (2.2.37)
Пример такой зависимости показан на рис. 2.12.
Для обработки результатов седиментационного анализа используется аналитический метод дифференцирования кинетической кривой.
|
В соответствии с (2.2.28) уравнение касательной для любого времени t имеет вид
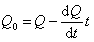 . (2.2.38)
. (2.2.38)
Производную dQ/dt можно найти, дифференцируя уравнение (2.2.33), при этом получаем
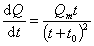 . (2.2.39)
. (2.2.39)
Подставляя в уравнение (2.2.38) значение Q из уравнения (2.2.33) и dQ/dt из уравнения (2.2.39), получаем
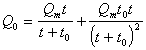 (2.2.40)
(2.2.40)
или после преобразования
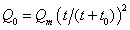 . (2.2.40)
. (2.2.40)
Тогда
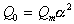 , (2.2.41)
, (2.2.41)
где 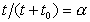 .
.
Время осаждения половины массы осадка t0 не может служить характеристикой дисперсности порошка, так как зависит от условий проведения опыта (вязкости среды, разности плотностей фаз и высоты осаждения). Поэтому его целесообразно заменить эквивалентной величиной, не зависящей от условий эксперимента, а связанной только с дисперсностью порошка.
Для этого в уравнении (2.2.17) равномерную скорость седиментации выразим как отношение высоты осаждения h ко времени осаждения, т. е. U= h/t.
С учетом этого для времени половинного осаждения
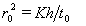 , (2.2.42)
, (2.2.42)
где r0 - размер частиц, полностью осевших к моменту времени половинного осаждения, K- константа седиментации.
Для любого момента времени 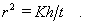
Следовательно, подставляя вместо t и t0 соответствующие значения r2 и 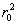 в уравнение (2.2.41), получаем
в уравнение (2.2.41), получаем
 . (2.2.43)
. (2.2.43)
Тогда
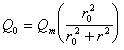 . (2.2.44)
. (2.2.44)
Последнее выражение представляет собой одну из модификаций аналитического уравнения Свен-Одена для интегральной кривой седиментации.
Дифференцируя это уравнение по r, получаем уравнение дифференциальной кривой распределения по размерам для полностью осевших частиц
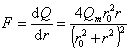 . (2.2.45)
. (2.2.45)
С учетом уравнения (2.2.43)
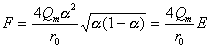 , (2.2.46)
, (2.2.46)
где 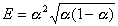 .
.
Так как параметр Е определяется только значением a и не зависит от условий проведения эксперимента, то для нахождения Е=f(a) используют табулированные значения.
Умножив найденные значения Е на 4Qm/r0, получают функцию распределения F. Уравнение (2.2.46) содержит постоянные Qm и r0 и переменную r. Обе постоянные этого уравнения независимы от условий опыта и могут быть приняты как основные характеристики дисперсной системы.
Прежде чем приступать к построению кривой распределения, следует установить значение трех основных радиусов, через которые должна пройти дифференциальная кривая распределения: предельные (минимальный rmin и максимальный rmax) и наивероятнейший rн, соответствующий максимальному значению дифференциальной функции распределения.
Из уравнения (2.2.44) следует, что при условии Q0 = 100, оседают самые малые частицы, имеющие радиус
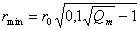 . (2.2.47)
. (2.2.47)
Дифференцируя уравнение (2.2.46), и учитывая, что при rн на кривой будет максимум, приравниваем первую производную нулю, получаем
rн = r0/2,24 (2.2.48)
и
rmax = 3 r0. (2.2.49)
Из уравнений (2.2.47) и (2.2.49) найдем степень полидисперсности системы, т.е. отношение максимального радиуса к минимальному:
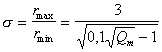 . (2.2.50)
. (2.2.50)
Степень полидисперсности зависит только от Qm, тогда как rнот r1/2, поэтому постоянные Qm и r0 называют соответственно коэффициентом полидисперсности и коэффициентом дисперсности.
Так как Q обычно выражают в процентах, а результаты экспериментальных наблюдений получают в единицах массы, нетрудно установить, что
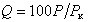 , (2.2.51)
, (2.2.51)
где Рк, Р – масса соответственно осевшей полностью и осевшей за время t дисперсной фазы.
Для нахождения Q необходимо определить Рк. Самый простой способ - дождаться конца осаждения, но это приводит к увеличению времени наблюдения, что иногда практически сделать нельзя. Тогда можно рассчитать Рк по уравнению
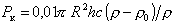 , (2.2.52)
, (2.2.52)
где R – радиус чашечки, м; h – высота осаждения, т.е. расстояние от поверхности жидкости до чашечки, м; с- концентрация твердой фазы, кг/ м3; r, r0 - табличные данные плотности твердой и жидкой фаз, соответственно, кг/м3.
Расчет Рк по уравнению (2.2.52) часто дает завышенные результаты, особенно в случае гидрофильных порошков, так как частицы, будучи покрыты тонкой адсорбционной сольватной оболочкой, не оказывают полного давления на дно чашечки. Поэтому поправку
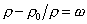 (2.2.53)
(2.2.53)
определяют другим приемом. Небольшую навеску порошка взвешивают сначала в воздухе, а затем в жидкой среде, в которой ведут седиментацию.
Тогда
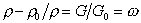 , (2.2.54)
, (2.2.54)
где G0, G – масса вещества, соответственно в воздухе и в жидкости.
Подставляя найденные значения w в уравнение (2.2.52), находят Рк, а затем рассчитывают Q по уравнению (2.2.51).
Получив кривую седиментации Q = f(t) в гравитационном поле, находят постоянные Qm и t0. Для этого используют построение зависимости в координатах уравнения (2.2.37).
Как следует из уравнения (2.2.37), Qm – котангенс угла наклона прямой, а t0/Qmотрезок, отсекаемый ею на оси ординат; умножением t0/Qm на Qm получают t0. В случае необходимости максимальное (конечное) время осаждения рассчитывают по уравнению (2.2.36).
|
Затем задаются рядом произвольных значений радиусов r, лежащих между rmin и rmax и проходящих через rн.
Полученные результаты используют для построения интегральной 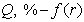 и дифференциальной
и дифференциальной 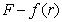 кривых распределения. Пример кривых распределения показан на рис. 2.13.
кривых распределения. Пример кривых распределения показан на рис. 2.13.

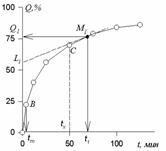
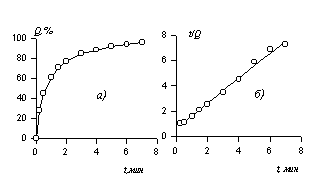 Рис. 2.12. Кинетическая кривая седиментации (а) и ее линейная форма (б)
Рис. 2.12. Кинетическая кривая седиментации (а) и ее линейная форма (б)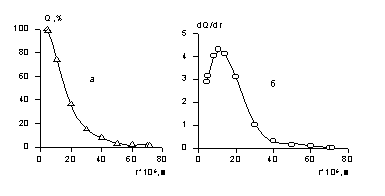 Рис. 2.13. Интегральная (а) и дифференциальная (б) кривые распределения частиц в суспензии по размерам
Рис. 2.13. Интегральная (а) и дифференциальная (б) кривые распределения частиц в суспензии по размерам
