Обменное взаимодействие

ОБМЕННОЕ ВЗАИМОДЕЙСТВИЕ, специфич. квантово-мех. взаимодействие тождественных частиц, в частности электронов. Является следствием принципа неразличимости частиц в квантовой механике и не имеет аналога в классич. физике. Суть принципа неразличимости сводится к требованию определенной перестановочной симметрии волновой функции системы тождественных частиц: для частиц с целочисленным спином (бозонов) волновая ф-ция должна быть симметричной, т.е. она не должна меняться при перестановке индексов частиц (координат и проекций спинов), а для частиц с полуцелым спином (фермионов) при такой перестановке волновая ф-ция должна менять знак, т. е. быть антисимметричной (см. Паули принцип). Наличие перестановочной симметрии налагает ограничения на взаимное пространств. расположение частиц, что приводит к изменению энергии квантовой системы по сравнению с аналогичной классич. системой частиц. Это изменение энергии обычно рассматривается как вызванное неким дополнительным квантовомсханическим взаимодействием, оно получило назв. "обменное взаимодействие", поскольку определяется членами в выражении для энергии системы, отвечающими перестановкам частиц (обмену частицами).

В химию понятие "обменное взаимодействие" было введено в 1927 В. Гайтле-ром и Ф. Лондоном в задаче расчета энергии основного состояния молекулы Н₂. Было показано, что возникновение обменного взаимодействия является причиной образования ковалентыой хим. связи. Пусть состояние электрона одного атома характеризуется волновой ф-цией j_A(r₁), электрона другого атома-ф-цией j_B(r₂). В нулевом приближении, т.е. при пренебрежении взаимод. между электронами, волновая ф-ция системы двух электронов равна произведению j_А(r₁) j_B(r₂). Вследствие квантовомех. неразличимости одинаковых частей этой же энергии будет отвечать волновая ф-ция j_A(r₂)j_B(r₁), соответствующая обмену электронов между атомами, т.е. имеет место т. наз. обменное вырождение. Ур-нию Шрёдингера будут удовлетворять две линейные комбинации этих ф-ций:

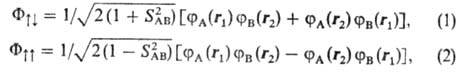
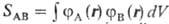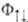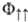где -интеграл перекрывания электронных волновых ф-ций атомов А и В (см. Молекулярные интегралы). Полная волновая ф-ция системы является антисимметричной относительно перестановок электронов (т.е. меняет знак при таких перестановках) и строится из произведений пространственных (координатных) ф-ций и на соответствующие спиновые ф-ции (спин-ф-ции). Из требования антисимметричности вытекает, что ф-ция 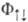отвечает противоположному направлению спинов электронов и полному электронному спину системы S=0 (синглет-ное состояние), ф-ция 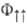-параллельно направленным спинам и полному электронному спину S= 1 (триплетное состояние). Энергия взаимод. атомов А и В в этих состояниях ( 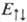и 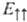соотв.) вычисляется как среднее значение оператора взаимод. U^{^}_вз:

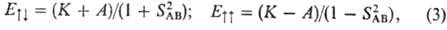
где

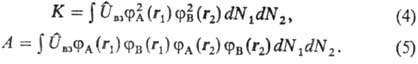
Интеграл К представляет классич. энергию кулоновского взаимод. пространственно распределенных зарядов; интеграл А наз. о б м е н н ы м и н т е г р а л о м, характеризует энергию обменного взаимодействия и не имеет классич. аналога. Он появляется вследствие того, что каждый электрон, как это следует из вида волновых ф-ций, с равной вероятностью может находиться как у атома А, так и у атома В. При этом в случае симметричной координатной ф-ции 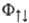вероятность для электронов расположиться в пространстве между ядрами увеличивается, а в случае антисимметричной ф-ции 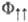уменьшается по сравнению с невзаимодействующей системой независимых атомов, т.е. появляются силы, к-рые имеют квантовомех. природу и воздействуют на электроны так, что изменяют вероятность их распределения в пространстве, а следовательно, и энергию взаимодействия. Эти силы и являются причиной возникновения обменного взаимодействия. И хотя полная энергия системы зависит от значения электронного спина, вследствие зависимости перестановочной симметрии координатной волновой ф-ции от полного электронного спина, энергия обменного взаимодействия не имеет отношения к взаимод. спинов, а является частью электростатич. энергии, к-рая обусловлена квантовой природой электронов.

Обменный интеграл (5) экспоненциально убывает с ростом расстояния между атомами, т.к. зависит от степени перекрывания волновых ф-ций. Поэтому обменное взаимодействие проявляется лишь при непосредственном сближении атомов. В отличие от электромагнитных и гравитационных сил, являющихся дальнодействующими, квантовые обменные силы относятся к близкодействующим, им присуще св-во насыщения. Энергия дальнодействующего взаимод. системы из N частиц пропорциональна числу разл. пар, к-рые можно составить из этих частиц, т.е. N(N — 1)/2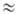 N²/2 при N >> 1, в то время как энергия обменного взаимодействия пропорциональна числу ближайших пар-соседей, т.е. она пропорциональна N.

В случае многоэлектронных систем знак энергии обменного взаимодействия зависит от строения электронной оболочки взаимод. объектов (атомов, молекул). Если взаимод. атомы с незаполненной валентной оболочкой, энергия обменного взаимодействия отрицательна (атомы притягиваются). Поэтому в согласии с (3) осн. энергетич. состояние большинства молекул синглетно. Обменное взаимодействие является главным стабилизирующим фактором при образовании ко-валентной связи. В случае систем с замкнутыми электронными оболочками энергия обменного взаимодействия положительна, обменное взаимодействие приводит к отталкиванию частиц. Именно такая ситуация имеет место при взаимод. инертных атомов или нейтральных молекул (см. Межмолекулярные взаимодействия).

Обменное взаимодействие определяет в значит. степени магн. св-ва в-ва. Так, состояние металлич. кристалла с параллельными спинами электронов (ферромагнитное) м. б. термодинамически более устойчиво, чем состояние с беспорядочно ориентированными спинами электронов, лишь в том случае, если обменный интеграл А положителен. Характерная для ферромагнетика точка Кюри (т-ра, выше к-рой у в-ва исчезают ферро-магн. св-ва) м. б. определена как т-ра, при к-рой энергия теплового движения атомов становится равной термодина-мич. выигрышу в энергии при параллельной ориентации спинов.

Лит.: Вонсовский С. В., Магнетизм, М., 1971; Давыдов А. С., Квантовая механика, 2 изд., М., 1973. И. Г. Каплан.