Квантовая механика
КВАНТОВАЯ МЕХАНИКА, изучает состояния микрочастиц и их систем (элементарных частиц, атомных ядер, атомов, молекул, кристаллов), изменение этих состояний во времени, а также связь величин, характеризующих состояния микрочастиц, с эксперим. макроскопич. величинами. Квантовая механика исследует уровни энергии, пространственные и импульсные характеристики систем частиц, эволюцию этих систем во времени, вероятности переходов между состояниями под влиянием взаимод. между системами и внеш. воздействий. В нерелятивистской квантовой механике для средних скоростей v всех частиц системы предполагается выполненным условие: (v/с)2<<1, где с - скорость света. Результаты нерелятивистской квантовой механики переходят в таковые классич. механики, когда выполняется принцип соответствия, т.е. когда произведение импульса каждой из взаимодействующих частиц на размер области, в к-рой это взаимод. существенно меняется, велико по сравнению с постоянной Планка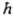
=1,0546.10-34 Дж.с.
Квантовая механика была сформулирована для объяснения явлений, к-рые не могли быть объяснены в рамках классич. механики и электродинамики. Трудами М. Планка (1900), А. Эйнштейна (1905, 1916) и Н. Бора (1912) было показано, что атомы имеют стационарные состояния, переходы между к-рыми происходят при излучении или поглощении кванта света, имеющего энергию 
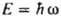и импульс 
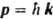, где w и k - круговая частота и волновой вектор световой волны соответственно. Проблема объяснения этих св-в атомов была решена почти одновременно с неск. сторон. Л. де Бройль (1924) предложил распространить волновые представления, привычные для описания электромагн. поля, на атомные частицы, сопоставляя своб. движению частицы с энергией Е и импульсом р волну
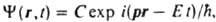распространяющуюся в пространстве и времени t (r-радиус-вектор частицы, i - мнимая единица, С - постоянный множитель). Тем самым он предсказал дифракцию таких частиц при рассеянии на кристаллах. В. Гейзенберг (1925) нашел матричное представление для динамич. переменных классич. механики, позволившее объяснить структуру уровней энергии нек-рых систем. Так возникла матричная механика. Э. Шрёдингер (1926) предложил дифференц. ур-ние, решениями к-рого при заданных граничных условиях являются собств. ф-ции y, названные волновыми ф-циями, и собств. значения, указывающие уровни энергии системы. Так возникла волновая механика. Анализ показал, что подходы В. Гейзенберга и Э. Шрёдингера эквивалентны, поэтому термины "матричная механика", "волновая механика" и наиб. употребительный сейчас "квантовая механика" являются синонимами. С вычислит, точки зрения, как правило, наиб. удобным оказывается метод решения ур-ния Шрёдингера.
Осн. постулаты квантовой механики. При рассмотрении задач о состояниях частиц и их систем осн. положения квантовой механики обычно формулируют в след, виде:
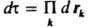- элемент объема в конфигурац. пространстве переменных N частиц, то величина |y(r1,...,rN; t)|2dt пропорциональна вероятности найти в момент времени t первую частицу вблизи точки с радиусом-вектором r1 в объеме dr1 (т. е. в параллелепипеде со сторонами dx1, dy1 и dz1, одной из вершин к-рого служит точка r1), вторую частицу - вблизи точки r2 в объеме dr2 и т.д. (М. Борн, 1926).
2. Каждой наблюдаемой физ. величине А (координате, импульсу, энергии и т.п.) сопоставляется линейный оператор
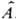. Для системы, находящейся в состоянии с волновой ф-цией y, при измерении величины А м.б. получены лишь те значения аi, к-рые являются собств. значениями оператора 
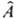, т. е. удовлетворяют равенству: 
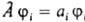, где ji нек-рая ф-ция от тех же переменных, что и волновая ф-ция системы. Вероятность найти значение аi определяется квадратом модуля интеграла 
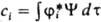, а среднее значение
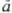- интегралом 
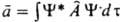, где j*i и y* - ф-ции, комплексно сопряженные ji и y. Поскольку величины аi и их среднее вещественны, на операторы 
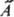накладывается дополнит. ограничение: они должны быть эрмитовыми. Это означает, что для любых ф-ций j и y должно выполняться соотношение: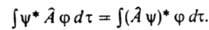 
3. Операторы
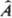, отвечающие наблюдаемым физ. величинам, к-рые определены в классич. механике (энергия, импульс и т. п.), получаются, если в соотношениях, установленных для этих величин классич. физикой, заменить координаты частиц операцией умножения на эти координаты, а импульсы - операцией дифференцирования (с точностью до множителя) по соответствующей переменной (т. наз. сопряженной координате). Напр., вместо координаты х употребляют оператор 
: 
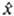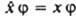; вместо компоненты импульса рх - оператор 
: 
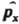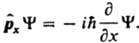Полученный при такой замене оператор соответствующей физ. величины должен быть записан так, чтобы он был эрмитовым. Так, операторы проекций момента кол-ва движения частицы записываются след. образом: 
, 
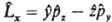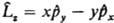и 
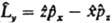. Собств. значения оператора 
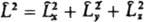, равные 
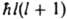, определяются неотрицат. целыми числами l, а собств. значения оператора проекции момента на к.-л. фиксированное направление, напр. ось z, - числами -l, -l+1,...,+l.
4. Волновые ф-ции y, описывающие состояния системы, являются решениями ур-ния Шрёдингера, или волнового ур-ния:
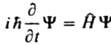
где
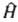-оператор полной энергии системы, наз. оператором Гамильтона или гамильтонианом; он получается из классич. ф-ции Гамильтона по правилам, указанным в п. 3.
5. У каждой элементарной частицы м.б. собств. момент кол-ва движения, не связанный с перемещением ее как целого. Этот момент наз. спином или собств. моментом кол-ва движения. Спин измеряется в единицах постоянной Планка и равен
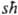, где s - характерное для каждого вида частиц целое или полуцелое неотрицат. число, наз. спиновым квантовым числом или просто спином. Проекция спина на любое фиксир. направление в пространстве может принимать значения (в единицах 
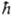) — s, —s+1,...,+s. Напр., спин электрона, протона и нейтрона равен 1/2, спин p-мезона-0, спин ядра атома дейтерия - l.
Т. обр., частица или система из неск. частиц может находиться в разл. квантовых состояниях, каждому из к-рых отвечает свое значение спина и его проекции. Это обстоятельство обычно отражается в том, что для каждой частицы вводится помимо трех пространств, переменных дополнит, четвертая переменная s, от к-рой зависят и спиновые операторы. Волновая ф-ция системы с учетом спина м. б. записана в виде:
y(r1, si; r2, s2;...; rN; sN; t)=y(1,2, ...,N; t). Системы тождеств, частиц (одной и той же массы, заряда и т.д.) с целочисленным спином подчиняются статистике Бозе - Эйнштейна, системы частиц с полуцелым спином -статистике Ферми-Дирака (см. Статистическая термодинамика). В свою очередь, симметрия волновой ф-ции системы тождеств. частиц полностью определяется типом статистики, к-рой подчиняются частицы: для частиц с целым спином волновая ф-ция симметрична, т.е. не меняется при перестановке индексов двух тождеств. частиц; для частиц с
полуцелым спином волновая ф-ция антисимметрична, т.е. меняет знак при любой такой перестановке (В. Паули, 1940). Перестановка индексов частиц означает переход к описанию того же состояния системы при др. порядке нумерации частиц.
Состояния квантовой системы, описываемые волновыми ф-циями, наз. чистыми состояниями. Для них имеется максимально полная информация о квантовой системе. Однако в квантовой механике возможно описание и таких состояний, с к-рыми нельзя сопоставить определенную волновую ф-цию, а можно только указать набор вероятностей |сi|2 появления при измерении к.-л. физ. величины А состояний, в к-рых эта величина принимает определенные значения. Для таких состояний нельзя построить волновую ф-цию в виде линейной комбинации волновых ф-ций ji чистых состояний с коэффициентами сi, поскольку известны лишь квадраты модуля этих коэффициентов, но неизвестны их фазы. Такие состояния наз. смешанными. Они м.б. охарактеризованы нек-рой операторной ф-цией, наз. матрицей плотности и позволяющей вычислять средние значения и вероятности разл. значений физ. величин в таком состоянии. Матрица плотности r зависит от тех переменных, к-рые определяют квантовую систему, и от времени; она удовлетворяет квантовому ур-нию Лиувилля: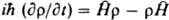
Ур-ние Шрёдингера и мат. аппарат квантовой механики. Ур-ние Шрёдингера является линейным дифференциальным и - что очень важно - однородным ур-нием. Это означает, что если y1 и y2 - к.-л. два решения этого ур-ния, то и любая их линейная комбинация c1y1+с2y2 с постоянными коэф. c1 и с2 будет также решением ур-ния Шрёдингера (т. наз. принцип суперпозиции). Если гамильтониан
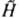не зависит в явном виде от времени (напр., для своб. молекулы или для молекулы, находящейся во внеш. стационарном поле), ур-ние Шрёдингера допускает разделение пространственных переменных, определяющих положения частиц, и времени. Волновая ф-ция состояния с энергией Ek (энергетич. уровень системы) принимает вид: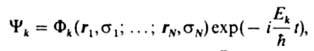
где ф-ция Фk удовлетворяет ур-нию
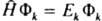, к-рое наз. стационарнымур-нием Шрёдингера. Вероятностная интерпретация квадрата модуля волновой ф-ции, сформулированная в п. 1 осн. постулатов квантовой механики для состояний системы с дискретным спектром уровней энергии, требует выполнения условия нормировки. Нормировка
волновой ф-ции на единицу возможна,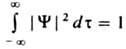
если соответствующий интеграл по всему конфигурац. пространству сходится, что имеет место всегда, когда модуль волновой ф-ции достаточно быстро убывает вне нек-рой конечной области (финитное движение). В этом случае энергетич. спектр, т. е. множество уровней энергии, оказывается дискретным, а волновые ф-ции, принадлежащие разл. уровням энергии (в общем случае-разл. собств. значениям эрмитова оператора), оказываются ортогональными:
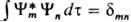, где dmn=1 при m=п и dmn=0 при т№п. В противном случае, когда частицы уходят на сколь угодно большое расстояние, напр., от места их столкновения (инфинитное движение), спектр собств. значений непрерывен, а нормировка и ортогональность волновых ф-ций таких состояний формулируется с помощью 5-ф-ции. Напр., для состояний частицы с определенными импульсами p' и р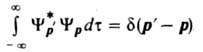
Волновая ф-ция, описывающая к.-л. состояние системы, определяется неоднозначно, но все такие описания эквивалентны, т. е. приводят к одинаковым наблюдаемым следствиям. Так, любую волновую ф-цию можно умножить на произвольный фазовый множитель ехр(iа), где a - действительная постоянная, не меняя средних значений любых операторов. Далее, любые преобразования систем отсчета, оставляющие инвариантным ур-ние Шрёдингера, преобразуют волновую ф-цию, но все получаемые при этом ее представления будут эквивалентными. И, наконец, волновая ф-ция м. б. задана в разл. формах при разл. представлениях пространства, на к-ром определяются волновые ф-ции; так, волновая ф-ция, заданная как ф-ция пространств. координат, т.е. в конфигурац. (или координатном) представлении, м. б. разложена в интеграл Фурье, так что коэффициенты этого разложения (т.е. ее фурье-образ) будут представлять волновую ф-цию того же состояния в импульсном представлении. Мат. аппарат квантовой механики определяется прежде всего тем, что наблюдаемые физ. величины представляются эрмитовыми операторами. Разл. соотношения между наблюдаемыми величинами должны сказываться на тех мат. соотношениях, к-рым подчиняются операторы. Если, напр., для рассматриваемого состояния системы волновая ф-ция является собст. ф-цией оператора
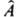нек-рой наблюдаемой величины А с собств. значением а, то в этом состоянии измерение величины А будет приводить к одному и тому же значению а. Измерение др. физ. величин F(k) будет также приводить к определенным значениям f(k) только в том случае, если эти величины имеют в рассматриваемом состоянии определенные значения. Это возможно, если отвечающие этим величинам операторы 
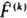коммутируют с оператором 
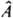, т. е. если выполняется соотношение: 
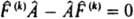. Если же нек-рый оператор
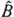не коммутирует с А, так что 
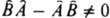, то не может существовать состояний системы, для к-рых А и В имеют одновременно определенные значения. В частности, не существует состояний, в к-рых координата и импульс частицы имели бы определенные значения, т. к. имеют место соотношения: 
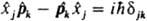, где индексы j и k принимают значения 1, 2, 3 и относятся к нумерации переменных: 
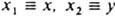и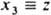 
. Из приведенных коммутационных соотношений для координат и импульсов следует, что в любом состоянии произведение среднеквадратичных разбросов координат Dr2 и импульсов Dp2 для каждой из частиц удовлетворяет соотношению: 
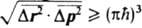. Это неравенство наз. соотношениемнеопределенностей для координат и импульсов. Следует подчеркнуть, что в квантовой механике подобного типа соотношение справедливо также для энергии системы и времени: 
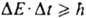, где DE - разброс в измеряемых значениях энергии, обусловленный взаимод. между измерит, прибором и исследуемой системой, Dt - длительность процесса измерения. Это же соотношение может иметь и др. смысл: в качестве DЕ может выступать неопределенность значения энергии нестационарного состояния замкнутой системы, тогда Dt будет тем характерным для данного состояния временем, за к-рое существенно меняются средние значения физ. величин. Соотношения неопределенностей для координат и импульсов, для энергии и времени имеют важное значение для понимания осн. положений квантовой механики и их интерпретации. Поэтому эти соотношения часто наз. принципом неопределенности.
Совокупность волновых ф-ций в заданном представлении (конфигурационном или импульсном), описывающих стационарные квантовые состояния системы из N частиц, наз. полной, если любая др. волновая ф-ция этой системы м. б. представлена в виде линейной комбинации или ряда, состоящего из таких ф-ций. Волновые ф-ции полной системы являются совместными собств. ф-циями 3N (без учета спина) или 4N (при учете спина) эрмитовых операторов, к-рые коммутируют между собой. Один из этих операторов - гамильтониан. Если одному и тому же уровню энергии системы отвечает неск. состояний, различающихся собств. значениями др. операторов, то такие уровни наз. вырожденными (см. Вырождение энергетических уровней).
Собств. значения ряда операторов либо пропорциональны целым числам, либо выражаются через целые числа. Такие числа наз. квантовыми числами; они часто служат для идентификации состояний квантовомеханич. системы. В ряде случаев набор квантовых чисел позволяет полностью задать состояние системы. Напр., для указания состояния
атома водорода достаточно четырех квантовых чисел: главное квантовое число n=1,2,... определяет спектр возможных энергий Еп=-R/n2, где R - постоянная Ридберга, равная 13,6 эВ (109737 см-1); азимутальное (или орбитальное) квантовое число l=0,1, ..., n—1 (при заданном п) определяет квадрат орбитального (углового) момента 
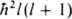; магн. квантовое число т=-l, -l(-)+1,..., l определяет проекцию 
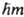орбитального момента на заданную ось; спиновое квантовое число s (- 1/2 или -1/2) определяет проекцию спина (
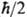или -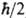
) на ту же ось. При описании молекул также используются квантовые числа, задающие, напр., состояния отдельных электронов (см. Орбиталь), возможные значения спина, орбитального и полного моментов, а также колебат. квантовые числа, характеризующие колебат. составляющую полной энергии, и вращат. квантовые числа, характеризующие вращат. составляющую полной энергии молекулы.
Точное решение ур-ния Шрёдингера удается найти лишь в редких случаях. Поэтому важное значение имеют разл. приближенные методы. Если при рассматриваемом движении импульсы частиц достаточно велики, а потенц. энергия их взаимод. изменяется медленно, то применимо квазиклассич. приближение. Оно позволяет, напр., рассчитывать вероятность прохождения частиц и квантовых систем через области пространства, к-рые недоступны для них согласно классич. механике вследствие недостатка энергии (см. Туннельный эффект). Иногда приближенные волновые ф-ции к.-л. состояния м.б. найдены в виде суперпозиции волновых ф-ций близкой, но более простой системы с коэффициентами, подбираемыми из условия минимума энергии системы (см. Вариационный метод). Если взаимод. в системе частиц записывается в виде суммы неск. частей, с одной из к-рых точное решение ур-ния Шрёдингера возможно, а остальные могут рассматриваться как малые возмущения первой, применяют возмущений теорию. Специфич. задачей квантовой механики является рассмотрение нестационарных волновых ф-ций, соответствующих переходам системы частиц из одного стационарного состояния в другое под влиянием нек-рого возмущения, зависящего от времени.
Релятивистская квантовая механика рассматривает квантовые законы движения микрочастиц, удовлетворяющие требованиям теории относительности. Осн. ур-ния релятивистской квантовой механики строго сформулированы только для одной частицы, напр, ур-ние Дирака для электрона либо любой др. микрочастицы со спином 1/2, ур-ние Клейна - Гордона - Фока для частицы со спином 0. Релятивистские эффекты велики при энергиях частицы, сравнимых с ее энергией покоя, когда становится необходимым рассматривать частицу, создаваемое ею поле и внеш. поле как единое целое (квантовое поле), в к-ром могут возникать (рождаться) и исчезать (уничтожаться) др. частицы. Последоват. описание таких систем возможно только в рамках квантовой теории поля. Тем не менее в большинстве атомных и мол. задач достаточно ограничиться приближенным учетом требований теории относительности, что позволяет для их решения либо построить систему одноэлектронных ур-ний типа, ур-ния Дирака, либо перейти к феноменологич. обобщению одноэлектронного релятивистского подхода на многоэлектронные системы. В таких обобщениях к обычному (нерелятивистскому) гамильтониану добавляются поправочные члены, учитывающие, напр., спин-орбитальное взаимодействие, зависимость массы электрона от его скорости (масс-поляризац. поправка), зависимость кулоновского закона взаимод. от скоростей заряженных частиц (дарвиновский член), электрон-ядерное контактное сверхтонкое взаимодействие и др.
Роль квантовой механики в химии. Большинство совр. теоретич. представлений о строении в-ва, переходов между разл. состояниями молекул и элементарных актах хим. р-ций основаны на квантовомех. понятиях. Совместно с квантовой или классич. статистикой квантовая механика позволяет развить представления и аппарат статистич. термодинамики и хим. кинетики. На основе представлений и с помощью методов квантовой механики разработан важный раздел теоретич. химии - квантовая химия, тесно связанная с классич. теорией хим. строения и экспериментально установленными закономерностями в хим. св-вах соединений. Квантовая механика служит основой теоретич. интерпретации атомных спектров и молекулярных спектров; она позволяет объяснить процессы, происходящие с в-вом при воздействии интенсивного излучения (см. Лазерная химия), поверхностные явления, металлич. проводимость и др., вести направленный поиск в-в с заданными св-вами. Результаты нерелятивистской квантовой механики находятся в согласии со всеми явлениями микромира; пока не обнаружено ни одного явления, к-рое потребовало бы ее дополнения или пересмотра. Перспектива развития квантовой механики заключается в уточнении методов расчета структуры молекул, разработке существующих и создании новых моделей для интерпретации явлений, характерных для систем большого числа частиц, в частности ферромагнетизма, сверхпроводимости.
===
Исп. литература для статьи «КВАНТОВАЯ МЕХАНИКА»: Дирак П. А. М., Принципы квантовой механики, пер. с англ., 2 изд., М., 1979; Ландау Л. Д., Лифшиц Е. М., Краткий курс теоретической физики, кн. 2 - Квантовая механика. 4 изд., М., 1972; Давыдов А. С.. Квантовая механика, 2 изд., М., 1973; Соколов А. А., Тернов И. М.. Жуковский В. Ч., Квантовая механика, М., 1979; Квантовая механика (терминология), под ред. Н.П. Клепикова, М., 1985 (КНТТ АН СССР); Клепиков Н. П., "Успехи физ. наук", 1987, т. 152, в. 3, с. 521-29. Н. П. Клепиков. Н. Ф. Степанов.
Страница «КВАНТОВАЯ МЕХАНИКА» подготовлена по материалам химической энциклопедии.
Активные темы форума
21 Фляги Ti