Квантовая химия

КВАНТОВАЯ ХИМИЯ, раздел теоретич. химии, в к-ром строение и св-ва хим. соединений, их взаимод. и превращения в хим. р-циях рассматриваются на основе представлений и с помощью методов квантовой механики. Квантовая химия тесно связана с экспериментально установленными закономерностями в св-вах и поведении хим. соед., в т. ч. с закономерностями, описываемыми классич. теорией хим. строения. Начало развитию квантовой химии положили работы ряда исследователей, выполненные в период становления квантовой механики. В. Гейзенберг (1926) впервые провел расчет атома гелия; В. Гайтлер и Ф. Лондон (1927) на примере молекулы водорода дали квантовомех. интерпретацию ковалентной связи. Их подход нашел дальнейшее развитие в работах Дж. Слейтера (1931) и Л. Полинга (1931) и получил назв. валентных связей метод. В этот же период Ф. Хунд (1928), Р. Малликен (1928), Дж. Леннард-Джонс (1929) и Э. Хюккель (1930) заложили основы широко распространенного в настоящее время молекулярных орбиталей метода. Одновременно появились и основополагающие работы Д. Хартри (1927) и В. А. Фока (1930), создавших самосогласованного поля метод, а также работы Дж. Слейтера (1929-30) по мат. основам конфигурационного взаимодействия метода. X. Бете (1929) и Дж. Ван Флек (1932-35) разработали кристаллического поля теорию, развитие к-рой привело к созданию поля лигандов теории, нашедшей широкое применение в координац. химии. Общая схема квантовохим. подхода. Квантовохим. рассмотрение атомов, молекул и более сложных систем, свободных или находящихся во внеш. поле, не зависящем от времени, обычно начинается с решения стационарного ур-ния Шрёдингера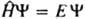

, где E и Y-полная энергия и волновая ф-ция системы,

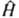-оператор Гамильтона (гамильтониан) системы, представляющий собой сумму операторов кинетич. и потенц. энергии электронов и ядер, входящих в систему. Оператор кинетич. энергии равен: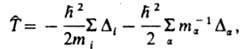

где индекс i нумерует электроны, индекс a-ядра, т и т_a- массы электрона и ядра а соотв.,

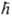- постоянная Планка. В декартовых координатах D_i и D_a представляют собой сумму вторых частных производных по координатам электрона i и ядра a соотв., напр.: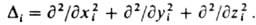

Оператор потенц. энергии равен сумме операторов кулоновского взаимод. частиц, к-рые зависят от расстояний r_ijмежду парами частиц, а также операторов взаимод. частиц с внеш. полем. Напр., для молекулы LiH (4 электтрона) в отсутствие внеш. поля гамильтониан выглядит след. образом:

При учете спина в гамильтониан входят также операторы спин-орбитального взаимодействия и спин-спинового взаимодействия. Волновая ф-ция для мол. системы, получаемая в результате решения ур-ния Шрёдингера, должна удовлетворять общим требованиям, предъявляемым к волновым ф-циям в квантовой механике. В частности, для многоэлектронной системы она должна быть антисимметричной относительно перестановки координат (пространственных и спиновых) любой пары электронов, т. е. должна менять знак при такой перестановке (см. Паули принцип). Задача нахождения волновой ф-ции и энергии мол. системы обычно решается с помощью вариационного метода или методов возмущений теории. Поскольку соответствующие расчеты весьма трудоемки, в зависимости от сложности объекта и целей исследования используют неэмпирические либо более простые полуэмпирические расчетные методы. В неэмпирических методах заранее задают только числа электронов и ядер в системе, а также заряды ядер и значения фундам. постоянных (напр., постоянной Планка, заряда и массы электрона). В полуэмпирических методах дополнительно из опыта заимствуются значения отдельных входящих в расчет величин, напр, величин, определяющих взаимод. электронов с ядрами, межэлектронное взаимод. и др. (см. Молекулярные интегралы). При этом вычисляемые величины, напр. энергия молекулы, взятой в качестве эталона, должны совпадать с эксперим. значениями. Неэмпирич. расчеты, называемые часто ab initio, получили широкое распространение лишь после достаточного развития вычислит. техники и сами в немалой степени способствовали этому развитию. Обычная схема введения упрощений при решении стационарного ур-ния Шрёдингера для молекулы сводится к следующему. В предположении, что центр масс молекулы находится в начале системы координат, вводят адиабатическое приближение, позволяющее решать задачу в два этапа: сначала рассмотреть систему электронов, движущихся в поле неподвижных ядер (электронное ур-ние Шрёдингера), а за тем - систему ядер, движущихся в усредненном поле электронов (ядерное ур-ние Шрёдингера). На первом этапе тем или иным способом (обычно с помощью прямого вариац. метода) находят волновую ф-цию системы из N электронов при разл. конфигурациях ядер для k-го электронного состояния Ф_k(r₁, r₂, ..., r_N; R), где r_i (i=1,2,...) - радиусы-векторы электронов, а R - совокупность переменных, определяющих положения ядер (напр., для заданной ядерной конфигурации совокупность независимых расстояний R_ab между парами ядер a и b. Одновременно получают и электронные энергии E_k(R), также зависящие от R. Ф-ция E_k(R) определяет тот потенциал, в к-ром движутся ядра молекулы в ее k-м электронном состоянии. С геом. точки зрения эта ф-ция представляет собой многомерную пов-сть, называемую поверхностью потенциальной энергии или потенц. поверхностью. Ф-цию E_k(R), вычисленную путем решения электронного ур-ния или найденную с помощью к.-л. модельных соображений (напр., в приближении многомерного гармонич. осциллятора), используют на втором этапе, решая волновое ур-ние для ядер, предварительно выделив ту часть гамильтониана, к-рая соответствует вращению системы ядер как целого. Получаемые при этом волновые ф-ции отвечают смещениям ядер друг относительно друга и обычно наз. колебат. волновыми ф-циями, а соответствующие им собств. значения-колебат. уровнями энергии. Совр. состояние и перспективы развития квантовой химии. Анализ электронного строения молекул (строения электронных оболочек, распределения электронной плотности и др.) позволил интерпретировать разл. типы хим. связей, мн. понятия классич. теории хим. строения и хим. кинетики, такие как валентность, кратность хим. связей, сопряжение и сверхсопряжение, энергия активации хим. р-ций и др. На начальных этапах развития квантовой химии были введены в химию новые понятия - гибридизация атомных орбиталей, s- и a-связи, трехцентровые связи, спин-орбитальное взаимод., электроотрицательность атомов, порядки связей, индексы реакц. способности и пр. Были установлены корреляции между вычисляемыми характеристиками (как правило, для равновесных конфигураций атомных ядер молекулы) и св-вами в-ва, а также его поведением в хим. р-циях, развита качеств, теория реакционной способности молекул. В 60-е гг. сформулирован и разработан принцип сохранения орбитальной симметрии в хим. р-циях (см. Вудворда-Хофмана правила). Квантовохим. расчеты поверхности потенц. энергии создали основу для решения задачи об особенностях движения (динамике) ядер частиц, участвующих в элементарном акте хим. р-ции. В результате стало возможным вычислять сечения р-ции и микроскопич. константы скорости, характеризующие переход из исходного квантового состояния системы в конечное (подробнее см. Динамика элементарного акта хим. р-ции). Благодаря развитию вычислит. методов и значит. совершенствованию неэмпирич. расчетов электронного строения молекул было установлено, что для достижения точности расчетов, сравнимой с точностью лучших эксперим. измерений, вариационные волновые ф-ции должны быть построены на значительно более широком базисе исходных ф-ций, чем при использовании методов мол. орбиталей, и содержать слагаемые, отвечающие не одной, а нескольким разл. конфигурациям электронной оболочки. Это позволяет получить более сложную картину электронного строения молекул, учитывающую локальное, а не усредненное по всем возможным положениям влияние электронов друг на друга, т.е. электронную корреляцию. Расчеты показывают, что во мн. случаях электронная корреляция определяющим образом влияет на энергетические и др. характеристики молекул. Квантовохим исследования позволили выявить ряд новых особенностей движения ядер частиц, составляющих молекулу. Так, было обнаружено наличие множественных минимумов на потенц. пов-стях, разделенных сравнительно невысокими потенц. барьерами. Кроме того, обнаружена высокая чувствительность электронного строения молекул в возбужденных состояниях к изменению конфигурации их ядер и к малым внеш. возмущениям. Переход к локализованным мол. орбиталям позволил по-ноаому оценить такие понятия классич. теории хим. строения, как двухцентровые связи, возбуждение той или иной отдельной связи или функц. группы в молекуле и т.п., а также подтвердил возможность использовать характеристики, относящиеся к данному мол. фрагменту (напр., параметры распределения электронной плотности, энергию фрагмента и др.), для всех молекул одного гомологич. ряда, включающих этот фрагмент. Вычислит. квантовая химия позволяет рассчитывать с достаточно высокой точностью такие важные характеристики молекул, как равновесные межъядерные расстояния и валентные углы, энергии хим. связей, барьеры внутр. вращения и барьеры перехода между разл. конформациями, энергии активации простейших хим. р-ций, а также величины, к-рые затруднительно или даже невозможно определить экспериментально (напр., энергии и геом. параметры молекул в возбужденных состояниях, вероятности квантовых переходов и т.п.). Квантовая химия позволяет учесть эффекты, связанные с проявлением взаимод. между разл. типами движений в молекулах. Было выяснено, в частности, в каких случаях адиабатич. приближение неприменимо и движение электронов и ядер следует рассматривать одновременно в их взаимодействии (см. Электронно-колебательное взаимодействие). Такое взаимод. в определенных случаях приводит к неустойчивости симметричной геом. конфигурации молекулы (эффекты Яна-Теллера). На основе квантовой химии разработана теория электронных спектров поглощения и люминесценции молекул, фотоэлектронных и рентгеноэлектронных спектров. Квантовая теория электрич. и магн. св-в молекул способствовала внедрению в химию физ. методов исследования, в частности ЭПР, ЯМР и ЯКР, и значительно облегчила интерпретацию эксперим. результатов. Получено большое число расчетных данных по вероятностям электронных переходов, временам жизни возбужденных состояний и спектроскопич. постоянным молекул. К числу осн. направлений развития квантовой химии относятся: всестороннее изучение влияния электронной корреляции на св-ва молекул в разл. состояниях и на особенности взаимод. молекул между собой; изучение связи разл. типов движений в молекулах и установление специфики состояний и св-в, в к-рых эта связь играет определяющую роль (напр., в случае неприменимости адиабатич. приближения); получение и накопление достоверных численных данных высокой точности по св-вам молекул, необходимых для решения прикладных вопросов; развитие теории колебательных и колебательно-вращат. спектров молекул, анализ особенностей колебат. движения при сильном возбуждении многоатомных молекул, переход к локальным колебаниям и др. В исследовании межмолекулярных взаимодействий задачи квантовой химии заключаются в нахождении потенциалов взаимод. при разл. ориентациях молекул, установлении зависимости этих потенциалов от строения молекул, создании моделей, позволяющих учесть влияние среды на св-ва молекул и механизмы элементарных процессов. Это позволит решить ряд проблем адсорбции и гетерог. катализа, поведения примесных молекул в твердом теле и др. Разработка этих направлений оказывает заметное влияние на развитие квантовой химии твердого тела. Изучение химии и физики плазмы, развитие лазерной техники, анализ процессов в атмосфере и космосе потребовали создания новых теоретич. методов, позволяющих исследовать эволюцию мол. систем на основе временного ур-ния Шрёдингера. Эти методы применяются, напр., при исследовании упругих столкновений атомов, ионов и молекул, развития мол. систем после импульсного их возбуждения лазерным излучением, при анализе динамики элементарного акта хим. р-ций, прежде всего газофазных. Квантовохим. представления и методы начинают активно применяться при изучении высокомол. соед. В частности, созданы адекватные модели для описания высокой проводимости орг. полимеров, переноса заряда по цепи полимера, а также ряда др. процессов. Методы квантовой химии используются в мол. биологии, напр. для расчета моделей биол. мембран, моделирования работы мышцы и др. Результаты квантовохим. расчетов совместно с данными, получаемыми методами теоретич. физики, начинают использовать в материаловедении для направленного создания материалов с заданными электрич. и магн. св-вами-сплавов, орг. полупроводников, композиц. материалов и др. Лит.. Цюляке Л., Квантовая химия, пер. с нем., т. 1, М., 1976; Минкин В. И., Сим кия Б. Я., Миняев P.M., Теория строения молекул. Электронные оболочки, М., 1979; Фларри Р., Квантовая химия. Введение, пер. с англ., М., I98S; Минкин В. И., Симкин Б. Я., Миняев Р. М., Квантовая химия органических соединений. Механизмы реакций, М., 1986; Берсукер И. Б., Электронное строение и свойства координационных соединений. Введение в теорию, 3 изд.. Л., 1986; Современные проблемы квантовой химии. Строение и свойства молекул, под ред. М. Г. Вё-селова. Л., 1986; Современные проблемы квантовой химии. Методы квантовой химии в теории межмолекулярных взаимодействий и твердых тел, Л., 1987. Н. Ф. Степанов, Н. Д. Соколов.

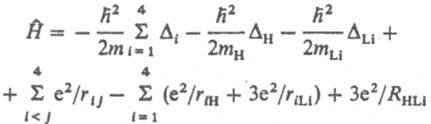
Ещё по теме

Квантовая химия — основы и применение

Квантово-химические методы в химии — применение и точность расчётов

Физическая химия — основы и методы исследования

Ядерная химия — открытия и методы исследования

Электронные представления в органической химии — от Беркенгейма до квантовой теории

Химическая физика — история и современные достижения

Химическая связь

Квантовая механика

Метод Хюккеля в квантовой химии

Химическая кинетика — основные понятия и законы

Квантовохимические расчёты в молекулярной спектроскопии

Теория химического строения органических соединений