ВВЕДЕНИЕ

Квантовая механика и статистическая физика в принципе позволя­ют дать исчерпывающее объяснение любым экспериментальным дан­ным о реакционной способности органических соединений и пред­сказать возможные направления реакций. Однако для реализации этих возможностей необходимо располагать очень мощными ЭВМ и доста­точно точными вычислительными методами. За последние годы в этих областях был достигнут существенный прогресс. Химические инсти­туты получили возможность широко использовать быстродейству­ющие ЭВМ, а благодаря быстрому развитию квантовой химии были разработаны достаточно эффективные полуэмпирические и неэмпири­ческие варианты метода молекулярных орбиталей (МО), которые можно использовать для изучения реакционной способности больших моле­кул, представляющих интерес не только для органической химии, но даже для биохимии. С их помощью удается установить, какие факторы определяют направление и относительный выход продуктов реакции, а также получить недоступную для эксперимента инфор­мацию о геометрии и электронной структуре переходных состояний. Однако в условиях многообразия и неравноценности квантовохимических методов представляется целесообразным охарактеризовать конкретные возможности каждого из них, отметить преимущества и недостатки и оценить перспективы развития путей их применения в органической химии.

Подробное описание теории МО можно найти в целом ряде монографий (см., например, [1, 2]). Однако при проведении приклад­ных квантовохимических расчетов нет необходимости углубляться в изучении ее основ. Необходимо иметь лишь общее представле­ние о теории МО, уметь пользоваться квантовохимическими про­граммами и научиться извлекать полезную информацию из резуль­татов расчета. Поэтому в настоящем разделе дано лишь краткое описание теории МО и расшифрованы сокращенные названия мето­дов, которые наиболее широко используются в отечественной и за­рубежной литературе в области органической химии.

В основе современной квантовой химии лежит уравнение Шрёдингера для стационарных состояний. Его обычно решают в адиабатическом приближении, т.е. в предположении, что ядерную и электронную волновые функции можно разделить и решать урав­нения для движения ядер и электронов раздельно. В этом прибли­жении уравнение Шрёдингера для электронной волновой функции записывается следующим образом:

ĤΨ=ЕΨ,                                                                                                             (1)

где Ĥ — гамильтониан системы, т.е. сумма операторов кинети­ческой и потенциальной энергий; Ψ=Ψ(х₁, x₂, …, х_n) — волновая функ­ция для системы из n частиц, которая зависит от их расположения в пространстве и спинов; Е — полная электронная энергия. Однако точно решить это уравнение удается лишь в случае одноэлектрон­ных систем. Поэтому в квантовохимических расчетах используются приближенные методы. Среди них наиболее широкое распространение получил метод Хартри—Фока [1, 2], или метод самосогласованного поля (ССП). В этом методе полагается, что каждый электрон дви­жется в поле атомных ядер, положение которых фиксировано в про­странстве, и в эффективном (усредненном) поле других электронов. Многоэлектронную волновую функцию ищут в виде антисимметризованнрго произведения спин-орбиталей, т.е. одноэлектронных МО φ_i(μ), умноженных на спиновые волновые функции α или β  соот­ветствующего электрона:

Ψ=Adet[φ₁(1)α(1)φ₁(1')β(1')…φ_n(n')β(n')],                                                             (2)

где 2n — число электронов в молекуле; μ — номер электрона. Значение коэффициента А определяется условием нормировки |Ψ|² к единице. В приближении Хартри—Фока уравнение Шрёдингера пере­ходит в систему интегрально-дифференциальных уравнений для движе­ния каждого отдельного электрона:  

Fφ_i=ε_iφ_i,                                                                                                                (3)

где F — фокиан (гамильтониан в приближении ССП), ε_i — энергии МО.

Молекулярные орбитали φ_i(μ) обычно ищут в виде линейных комбинаций атомных орбиталей (ЛКАО) χ_i(μ)

φ_m(μ)=∑C_miχ_i(μ),                                                                                                   (4)

где C_mi — искомые коэффициенты.

Таким образом, совокупность атомных орбиталей (АО) χ_iявля­ется физически наглядным базисом для построения молекулярной волновой функции φ_m. Обычно количество базисных АО недоста­точно велико, т.е. базис является неполным. Основное требование к неполному базисному набору АО заключается в том, чтобы он мог достаточно точно передать распределение электронной плотности в молекуле, т.е. базис должен быть достаточно сбалансированным. К сожалению, на практике выполнить это условие бывает трудно. Атомные орбитали хорошо аппроксимируют распределение электрон­ной плотности в изолированных атомах, но их использование при расчетах волновых функций молекул может приводить к погрешностям, связанным с неспособностью передать некоторые особенности измене­ния электронного распределения при образовании валентных связей. Поэтому в случае молекул приходится расширять атомные базисные наборы χ_iпутем включения в них дополнительных функций.

Для определения коэффициентов C_miиспользуется вариационная процедура минимизации полной электронной энергии молекулы Е. Рутан показал [З], что коэффициенты C_mi, соответствующие минимальной величине, могут быть определены из следующей системы уравнений:

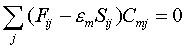,                                                                                              (5)

где

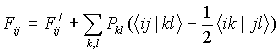; условие нормировки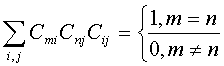

Суммирование ведется по всем базисным орбиталям  χ_i, χ_j, χ_kи χ_l;

S_ij — интервал перекрывания АО χ_i и χ_j, F'_ij — матричный эле­мент одноэлектронного гамильтониана, в который включены кинетическая энергия электронов и энергия взаимодействия электронов и атомных ядер; P_kl — матрица зарядов и порядков связей; <ij|kl> — интеграл кулоновского взаимодействия двух электронов:

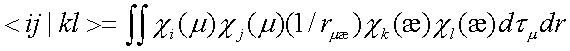.                                 (6)

В этом выражении интегрирование производится по всему прост­ранству декартовых координат: r_μæ — расстояние между электронами μ и æ.

Для решения нелинейной системы уравнений (5) применяется метод самосогласования, в котором в качестве нулевого приближения берется совокупность коэффициентов C_mi, причем выбор их может быть довольно произвольным. По коэффициентам нулевого приближения строят матрицу F_ij; по ней, решая уравнения (5), находят набор коэффициентов C_mi, который используют для построения новой матрицы F_ijи т.д., пока матричные элементы F_ijи коэффициенты C_mi не перестанут изменяться.

На практике обычно пользуются как полуэмпирическими, так и неэмпирическими методами. Они различаются методикой вы­числения матричных элементов, описывающих взаимодействие элект­ронов между собой и электронов и атомных ядер в уравнениях (5). В полуэмпирических методах для этой цели используются приближен­ные эмпирические формулы и известные из эксперимента параметры атомов. В неэмпирических методах проводится непосредствен­ный аналитический расчет матричных элементов. Для неспециалиста название "неэмпирический" является синонимом слова "точный", но в действительности это не так. Неэмпирические методы также являются приближенными, прежде всего из-за неполноты ис­пользованного базиса. Большинство неэмпирических расчетов проводят в базисах небольшого и среднего размеров. Это вносит су­щественную ошибку в результаты расчета, так как такие базисные наборы не могут передать некоторые особенности распределения электронной плотности в молекулах. В результате все без исключения параметры молекул вычисляются с некоторой ошибкой. Было бы желательно (хотя на практике это сделать очень трудно из-за больших затрат машинного времени) использовать достаточно большие базисы, которые обеспечивают выход на так называемый хартри-фоковский предел, когда дальнейшее увеличение числа базисных орбиталей не влияет на полученные результаты. Но даже в этом случае мы найдем не точное решение уравнения Шрёдингера, а лишь его решение в приближении Хартри-Фока. Для получения точного решения уравнения Шрёдингера необходимо еще учесть электронную корреляцию (см. ниже).

Полуэмпирические расчеты в настоящее время чаще всего про­водят в валентных приближениях ППДП, ЧПДП и ПДДП [4].

В перечисленных выше приближениях волновые функции рас­считывают только для валентных электронов, а электроны внутрен­них оболочек включают в остов молекулы; используют минималь­ный слейтеровский базис; пренебрегают некоторой частью матрич­ных элементов кулоновского взаимодействия электронов. Послед­нее допущение является наиболее существенным, так как оно по­зволяет значительно упростить расчет. Количество матричных элементов кулоновского взаимодействия электронов (6) очень велико, оно пропорционально числу базисных орбиталей в четвертой сте­пени, поэтому при увеличении базиса в 2 раза необходимо вы­числить в 16 раз больше кулоновских интегралов (6). Их расчет требует очень больших затрат машинного времени и для многих соединений, представляющих интерес с точки зрения органической химии, на современных ЭВМ практически неосуществим.

В полуэмпирических методах пренебрегают большей частью кулоновских интегралов (6), которые имеют небольшую абсолютную величину, но точность расчета при этом заметно снижается (величина каждого кулоновского интеграла, которым пренебрегают, мала, но их количество велико). Это удается частично ком­пенсировать за счет удачного подбора параметров. В приближении ППДП учитываются только одноцентровые интегралы типа <ii|ii> и двухцентровые интегралы типа <ii|kk> (χ_i и χ_k принадлежат разным атомам). В приближении ЧПДП дополнительно учитываются кулоновские интегралы, у которых все четыре орбитали χ_i, χ_j, χ_kи χ_lпринадлежат одному атому. В приближении ПДДП, кро­ме интегралов, которые учитываются в приближениях ППДП и ЧПДП, в расчет дополнительно включаются интегралы <ik|jl>, у которых орбитали χ_i и χ_kпринадлежат одному атому, а χ_j и χ_l— другому.

Для вычисления одноцентровых матричных элементов в полуэмпирических методах, как правило, используются данные эксперимента по атомным спектрам, а двухцентровые обычно рассчитывают по эмпирическим формулам, которые приближенно отражают зависимость взаимодействия электронов и атомных ядер и электро­нов между собой от взаимного расположения атомных орбиталей.

Для определения параметров двухцентровых интегралов, входя­щих в эмпирические формулы, приходится привлекать данные не только для атомов, но и для малых молекул. При этом задача решается неоднозначно и различия в способах подбора параметров характеризуют модификации методов ППДП, ЧПДП и ПДДП. Рациональ­ней подбор параметров позволяет смягчить недостатки приближений ППДП, ЧПДП и ПДДП и даже самого метода ССП.

Для расчета свойств основного состояния органических молекул в настоящее время широко используются следующие полуэм­пирические методы: ППДП/2 [5, 6] и ППДП/БУ [7] (приближение ППДП), ЧПДП [8] и различные варианты метода МЧПДП [9 — 13] (приближение ЧПДП), МПДП и AM1 [14—16] (приближение ПДДП). Параметры в методах ППДП/2 и ЧПДП подобраны так, чтобы воспроизвести распределение электронной плотности в малых моле­кулах, которое дает неэмпирический расчет в минимальном слейтеровском базисе. Эти методы позволяют рассчитать геометрию и дипольные моменты молекул. Их можно использовать для расчета индексов реакционной способности, но для вычисления поверхностей потенциальной энергии органических реакций и пара­метров переходных состояний данные методы не годятся.

Параметры в методе ППДП/БУ подобраны так, чтобы воспроизвести кривые Морзе для двухатомных молекул. Этот метод позволяет рассчитать геометрию, потенциалы ионизации и энергии атомизации молекул, но хорошее согласие с экспериментом получается только для малых молекул. С увеличением размера молекулы расхождение данных расчета и эксперимента становится больше. Кроме того, метод ППДП/БУ существенно переоценивает стабильность переходных состояний для большинства органических реакций. Параметры, которые используются в методах МЧПДП/2, МЧПДП/3, МПДП и AM1 для оценки величины матричных элементов, подобраны так, чтобы воспроизвести геометрию и теплоты образования органических соединений. Кроме геометрии и теплот образования, эти методы позволяют неплохо вычислить потенциалы ионизации и дипольные моменты молекул, а также геометрию переходных состояний и энергии активации. В настоящее время их довольно широко используют для расчета поверхностей потенциальной энергии органических реакций. В большинстве случаев получаются удовлетворительные результаты. При вычислении геометрии и относительной стабильности интермедиатов и переходных состояний метод МПДП обычно дает лучшее согласие с экспериментом по сравнению с методами МЧПДП/2 и МЧПДП/3. Это связано, по-видимому, с более точным учетом кулоновского взаимодействия электронов.

Расчетов с использованием метода AM1 пока опубликовано очень мало, поэтому мы не можем охарактеризовать область его при­менения. По-видимому, он дает примерно такие же результаты, как метод МПДП. Метод AM1 отличается от МПДП способами подбора параметров и формулой для вычисления энергии отталкивания остова. За счет более совершенной методики подбора параметров удается немного повысить точность вычисления теплот образования молекул, содержащих атомы кислорода и азота. За счет изменения формулы для вычисления энергии отталкивания остова удалось несколько улучшить согласие с экспериментом при расчете межмолекулярных взаимодействий. Однако количественное улучшение согласия с экспериментом, которое при этом получается, по имеющимся в настоящее время данным невелико.

В неэмпирических методах все матричные элементы взаимодействия электронов и атомных ядер и электронов между собой вычисляются с помощью аналитического расчета необходимых интегралов в некотором базисе АО. Наиболее точно распределение электронной плотности в атомах можно передать с помощью слейтеровских АО, т.е. функций типа ехр(-αr), rехр(-αr), хехр(-αr), yехр(-αr) и т.д. Однако со слейтеровскими орбиталями очень трудно вычислить интегралы, которые входят в фокиан для молекул. Поэтому в качестве базисных АО обычно берут гауссовы функции — для s-орбиталей: ехр(-αr²);

для p-орбиталей: xехр(-αr²), yехр(-αr²), zехр(-αr²);

для d-орбиталей: x²exp(-αr²), y²exp(-αr²), z²exp(-αr²), xyexp(-αr²), xzexp(-αr²), yzexp(-αr²).

Это так называемые примитивные гауссовые функции. С ними отно­сительно легко вычислять матричные элементы, но, когда их мало, они плохо воспроизводят распределение электронной плотности в атомах и молекулах. В связи с этим гауссовых орбиталей приходится брать намного больше, чем слейтеровских. Обычно исполь­зуют так называемые сгруппированные базисы, в которых каждая базисная орбиталь представляет собой линейную комбинацию из нескольких примитивных гауссовых функций.

В настоящее время для изучения реакционной способности и строения органических соединений наиболее широко используются базисы, предложенные Поплом с сотр.: минимальный базис ОСТ-3ГФ, валентно-расщепленные базисы 3-21ГФ, 4-31ГФ, 6-31ГФ, валентно-расщепленные базисы с поляризационными орбиталями 6-31ГФ* и 6-31ГФ**, валентно-расщепленные базисы с диффузными s- и p-орбиталями 3-21+ГФ и 4-31+ГФ [17—21].

ОСТ-ЗГФ — минимальный базис, в котором каждая слейтеровская орбиталь аппроксимирована линейной комбинацией из трех гауссовых функций.

3-21ГФ, 4-31ГФ, 6-31ГФ — валентно-расщепленные базисы, в которых каждая слейтеровская орбиталь для электронов внутренних оболочек аппроксимирована линейной комбинацией соответственно из трех, четырех и шести гауссовых функций, а для валентных электронов вместо каждой слейтеровской орбитали используются две линейные комбинации гауссовых функций: одна — из двух (базис 3-21ГФ) или трех (базисы 4-31ГФ и 6-31ГФ), а другая — из одной примитивной гауссовой функции. В этих трех базисах одинаковое число сгруппированных гауссовых функций, но число примитивных функций в базисах 6-31ГФ и 4-31ГФ больше, чем в базисе 3-21ГФ.

Использование базисов 6-31ГФ и 4-31ГФ позволяет получить более точную аппроксимацию распределения электронной плотности, особенно вблизи атомных ядер, однако точность результатов при вычислении большинства физико-химических параметров молекул повышается незначительно, а затраты машинного времени возрастают существенно (наиболее сильно в расчетах с оптимизацией геометрии). Поэтому в прикладных работах в настоящее время наиболее широко используется базис 3-21ГФ.

6-31ГФ* и 6-31ГФ** - валентно-расщепленные базисы с поляризационными d-орбиталями. В базис 6-31ГФ* включены поляризационные d-орбитали на р-элементах, т.е. на атомах углерода, азота и т.д., а в базис 6-31ГФ** — d-орбитали на р-элементах и р-орбитали на атомах водорода. Включение в базис поляризационных орбиталей существенно повышает точность расчета, но, к сожалению, при этом очень сильно возрастают затраты машинного времени.

3-21+ГФ и 4-31+ГФ – с дополнительными диффузными s- и р-орбиталями – используются в квантовохимических расчетах  физико-химических параметров анионов. При образовании аниона из электрически нейтральной молекулы МО становятся более диффузными. Этот эффект не удается передать при использовании валентно-расщепленных базисов, подобранных для расчета незаряжанных молекул, поэтому точность неэмпирического расчета для анионов в таких базисах оказывается существенно ниже, чем для нейтральных соединений. Повышение точности может быть достигнуто за счет дополнительного включения в базис диффузных s- иp-орбиталей. Это наиболее экономичный способ повышения точности неэмпирических расчетов для анионов. Затраты машинного времени при этом возрастают лишь в 1,5 раза. При изучении анионов можно также использовать базисы с поляризационными орбиталями, так как d-орбитали на р-элементах и р-орбитали на атомах водорода являются диффузными функциями, но в этом случае затраты машинного времени на выполнение расчета возрастают сильнее.

Таким образом, мы видим, что все неэмпирические квантово-химические методы являются в большей или меньшей степени приближенными и их результаты очень сильно зависят от выбора базиса. Увеличение числа базисных функций обычно позволяет точнее передать распределение электронной плотности в молекулах и его изменение в ходе химических реакций. Вообще говоря, желательно расширять базис до выхода на хартри-фоковский предел. Однако сделать это удается лишь для простейших молекул. Для более сложных соединений приходится идти на компромисс между точностью расчета, с одной стороны, и затратами машинного времени (стоимостью расчета,  возможностями ЭВМ) - с другой. Поэтому при изучении таких соединений приходится ограничиваться базисами среднего и даже минимального размеров, но тогда в расчет вносится значительный элемент произвола и теряется его универсальность, т.е. оказывается, что различные параметры молекул нужно рассчитывать в разных базисах.

Кроме того, использование приближения Хартри-Фока (метода ССП) также может вносить немалую ошибку в результаты расчета. В этом приближении вероятность найти электрон в некоторой точке пространства не зависит от местонахождения других электронов, распределение в пространстве которых задано одноэлектронными волновыми функциями. В результате двум электронам с одинаковыми спинами не запрещено занимать одну и ту же точку пространства. В действительности электроны с одинаковыми спинами стремятся избежать находиться не только в одной точке пространства, но даже близко друг от друга. Другими словами, электроны движутся зависимо, т.е. их движение носит коллективный характер. Пренебрежение этим эффектом, который принято называть электронной корреляцией, приводит к существенному завышению энергии взаимодействия электронов и, как следствие, завышению полной энергии молекулы.

Учет электронной корреляции является весьма трудоемкой задачей, требующей очень больших затрат машинного времени. Для этой цели в настоящее время чаще всего используют различные варианты метода конфигурационного взаимодействия, теории возмущений или метода электронных пар. В методе конфигурацион­ного взаимодействия [1] многоэлектронную волновую функцию Ф ищут в виде линейной комбинации большого числа детерминантов Ψ_k:

Ф=∑C_kΨ_k,                                                                                                            (7)

где C_k— коэффициенты разложения; Ψ_k(где k≥1) — детерминанты, которые построены из одноэлектронных волновых функций основного состояния и отличаются от Ψ_o(волновой функции основного состояния, рассчитанной в приближении Хартри-Фока) тем, что один, два или более электронов перешли с занятых МО на вакантные.

Расчеты по теории возмущений основаны на предположении, что электронная корреляция относительно мало меняет волновую функцию основного состояния. В программе ГАУССИАН-80, которая наиболее широко в настоящее время применяется для неэмпирических квантово-химических расчетов, корреляционные поправки учи­тываются по теории возмущений Мёллера—Плезетта. В работах [22, 23] был предложен вариант метода МПДП с учетом электронной корреляции по теории возмущений Бриллюэна—Вигнера (КМПДП).

В методе электронных пар использовано формальное выраже­ние, в котором корреляционная энергия записана как сумма кор­реляционных эффектов от каждой электронной пары [24]. Простейшим вариантом этого метода является приближение независимых электронных пар (в зарубежной литературе принято сокращенное обозначение IEPA). В данном приближении не учитывается взаимо­действие электронных пар, поэтому уравнение для каждой электронной пары решается отдельно, а полная корреляционная энергия вычисляется как сумма корреляционных энергий всех электронных паp. IEPA является относительно дешевым (с точки зрения затрат машинного времени) методом учета корреляционных эффектов, но энергия электронной корреляции в этом приближении получается сильно завышенной.

В приближении связанных электронных пар (в зарубежной литературе принято сокращенное обозначение СЕРА) [25] учитывается взаимодействие электронных пар, поэтому уравнения можно решить только с помощью итерационной процедуры. Результаты получаются более точными, но затраты машинного времени на такой расчет необычайно велики. Так, расчет с учетом энергии электронной корреляции методом СЕРА для переходного состояния в реакции Сl^- + СН₃Сl = ClСН₃ + Сl^-c фиксированной геометрией потребовал свыше 10 ч на ЭВМ с быстродействием около 10 млн операций в секунду (для сравнения расчет для этого переходного состояния без учета энергии электронной корреляции на аналогичной ЭВМ требует 15—20 мин).

Во Введении мы дали краткое описание квантово-химических методов. Более детальное знакомство с ними практически не тре­буется для решения прикладных задач. Это связано с тем, что на основе анализа приближений, сделанных при разработке того или иного квантово-химического метода, как правило, не удается установить область его применения и очертить круг задач, кото­рые можно решить с его помощью. К сожалению, многие квантово-химические методы, которые лучше обоснованы с теоретической точки зрения, на практике дают плохие результаты и поэтому не применяются, а более грубые модели с удачно подобранными параметрами широко используются. Это связано с тем, что в любом квантово-химическом методе сделано достаточно много различных приближений. В некоторых методах ошибки, к которым приводят эти приближения, частично компенсируют друг друга и в результате получается хорошее согласие с экспериментом. Сказать зара­нее, будет или не будет иметь место такая компенсация, нельзя, поэтому выяснить область применения и охарактеризо­вать точность каждого конкретного метода можно лишь на основе численного эксперимента и систематизации опубликованного расчетного материала. Знание этого вопроса (какие параметры молекулы каким методом следует вычислять и какие при этом могут получиться ошибки) отличает "опытного" квантового химика от "неопытного". В следующих разделах книги мы постараемся помочь нашему читателю стать "опытным" квантовым химиком.