Электронная плотность

ЭЛЕКТРОННАЯ ПЛОТНОСТЬ, плотность вероятности распределения электронов в квантовой системе (атоме, молекуле, кристалле). В квантовой химии в понятие электронной плотности вкладывают неск. смыслов. Если система N электронов описывается волновой ф-цией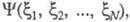 где символом 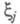обозначен набор всех координат электрона, включая спиновую координату 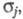то обычно задают электронную плотность как ф-цию радиус-вектора электрона r (r = r₁)

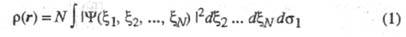
(интегрирование ведется по всей области изменения указанных переменных). Поскольку согласно Паули принципу ф-ция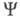 антисимметрична относительно перестановок электронных переменных, 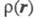не зависит от того, координаты какого именно электрона фигурируют в ее определении. Электронная плотность 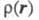отражает пространственное распределение заряда и электрич. св-ва частицы (дипольный момент и т. п.), ее наз. также зарядовой плотностью.
Если в выражении (1) при интегрировании по спиновой переменной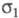 учитывать, что проекции спина на выделенную ось различны, то 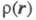определяется как спиновая плотность и отражает пространственное распределение спина в мол. системах с ненулевым суммарным спином (радикалы, триплетные возбужденные состояния молекул и др.). Спиновая плотность м. б. изучена экспериментально методами ЭПР.
В экспериментах по рассеянию электронов или по ионизации молекул электронным ударом данные об энергетич. распределении электронов позволяют оценить импульсную электронную плотность, к-рая определяется ф-лой (1), при условии, что координатное представление ф-ции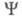заменено на импульсное, т. е. в роли 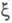использованы вектор импульса электрона Р и спин. Величина р(Р) позволяет находить кинетич. энергию и импульсы электронов системы.

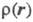лектронную плотностьчаще всего получают с помощью рентгенографич. экспериментов - т. наз. форм-факторы отвечают фурье-обра-зу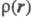(см. Рентгеновский структурный анализ). Зависимость электронной плотности от положений ядер усреднена при этом по термодина-мич. ансамблю, т. е. определяется с поправкой на тепловое движение. Оценки 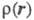представляют картами типа топографических, на к-рых для определенных сечений трехмерного пространства задаются линии уровня электронной плотности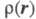= const. Как правило, электронная плотность имеет максимумы лишь в точках R_a, отвечающих положениям ядер, и хотя в целом электронная плотность- гладкая ф-ция, в указанных точках она имеет особенности: вдоль любого направления, выходящего из точки R_a, модуль градиента электронной плотности не равен нулю и пропорционален заряду ядра Z_a (т. наз. условие Като). Нек-рые из ядер на картах электронной плотности соединены "хребтами", к-рые можно соотнести с хим. связями. Такое соотнесение естественно, поскольку топология электронных распределений существенно меняется лишь при таких изменениях ядерной конфигурации, к-рые можно связать с изменением системы связей. Приводят и разностные карты электронной плотности молекул и образующих их атомов, позволяющие судить об особенностях перераспределения электронной плотности при образовании молекул или кристаллов из атомов.

С электронной плотностью обычно связывают эффективные заряды на атомах. Так, если с атомом соотнести нек-рую пространств. область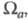, то эффективный заряд Q_a можно определить как 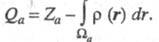Область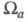и заряд Q_a зависят от геометрии молекулы (и способа выделения 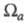причем атому, вообще говоря, может отвечать неограниченная область пространства). В экспериментах по ЯМР, ЯКР и мёссбауэровской спектроскопии изменение электронной плотности вблизи ядра нередко интерпретируют с помощью зарядов на атомах. Распределение электронов в области внутр. оболочек атома меняется под действием соседних ядер, что определяется по данным фото- и рентгеноэлектронной спектроскопии. Эти явления также описывают как изменение зарядов на атомах. Все указанные заряды определяются поведением электронной плотности в разл. областях пространства и, вообще говоря, не коррелируют друг с другом или с дипольным моментом мол. системы.

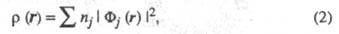
где заселенности п_j - неотрицат. числа, не превосходящие 2, причем сумма всех заселенностей (при бесконечном, вообще говоря, числе значений j)равна N. В приближении мол. орбиталей все занятые орбитали системы можно считать натуральными. Переход к локализованным орбиталям позволяет описать электронную плотность вблизи ядра неск. орбиталями, соотносимыми с хим. связью, или неподеленной парой электронов. При моделировании натуральных орбиталей нередко используют гибридные орбитали (см. Гибридизация атомных орбиталей). В рамках ЛКАО-приближения электронную плотность определяют через коэф. разложения в ряд натуральных мол. орбиталей по атомным орбиталям, причем пространств. область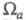 соотносится с областью локализации атомной орбитали. Симметрия мол. орбиталей позволяет разбить электронную плотность на вклады, создаваемые 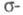и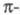электронами, и анализировать их раздельно, учитывая при необходимости их взаимное влияние (напр., индукционное) (см.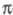-Электронное приближение).
Согласно теореме Хоенберга-Кона, для основного состояния молекулы электронная плотность отражает всю специфику молекулы. Напр., при r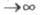 электронная плотность экспоненциально спадает, причем показатель экспоненты пропорционален потенциалу ионизации. Делаются попытки соотнести энергию молекулы с величиной 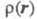в рамках к.-л. из вариационных методов (т. наз. методы функционалов плотности), одним из первых вариантов к-рых можно считать приближение Томаса-Ферми; иногда к этим методам относят самосогласованного поля метод.
Электронная плотность- важная физ. характеристика мол. системы, анализ к-рой позволяет соотнести хим. строение молекулы с локальными особенностями электронного распределения. Перераспределение электронной плотности молекулы по сравнению с электронной плотностью входящих в ее состав атомов отражает характер хим. связи и позволяет судить о взаимном влиянии атомов, изменении строения того или иного мол. фрагмента в ряду родственных молекул. Методы изучения и анализа электронной плотности интенсивно развиваются.

Лит. см. при ст. Квантовая химия.

В. И. Пупышев.