4.4. Основы построения детерминированных математических моделей элементов ХТС
Как было сказано выше, детерминированные или физико-химические математические модели отражают теоретические закономерности процессов, протекающие в элементах ХТС. При разработке таких моделей используют законы сохранения массы и энергии, законы переноса вещества, энергии и импульса, закономерности кинетики протекающих химических реакций, гидродинамику потоков и т.д. В связи со сложностью реальных технологических процессов, при разработке их математических моделей обычно вводят ряд допущений, упрощающих описание реального процесса, и позволяющих применить блочный принцип построения моделей, согласно которому математическое описание объекта в целом получают как совокупность описаний отдельных элементарных процессов, протекающих в рассматриваемом объекте. Рассмотрим основы построения детерминированных математических моделей процессов на некоторых примерах.
Модуль смесителя:
Модуль смесителя является одним из наиболее простых модулей. В соответствии с исходной задачей, два потока вещества, имеющие расходы G1 и G2(моль/сек), температуры T1 и T2 (град.К), составы X1i и X2i(мольные доли), теплоту Q1 и Q2(Вт) подаются в смеситель, откуда выходит один поток с расходом G3, температурой T3, составом Х3i и теплотой Q3(см.Рис.4.11).
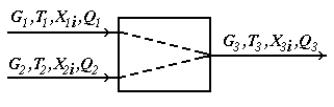
Рис.4.11. Схема модуля смесителя
Физико-химическая модель смесителя предназначена для расчета материального и теплового балансов процесса смешения двух потоков вещества. Существуют модули для смешения нескольких потоков вещества, но они являются расширенной модификацией смесителя для смешения двух потоков.
Обычно при составлении упрощенной детерминированной модели принимаются некоторые допущения. Для смесителя, допущения будут следующие:
1) Структура потока в аппарате соответствует режиму идеального смешения;
В противном случае, поток на выходе смесителя будет не полностью перемешанный, и, в таком случае необходимо будет либо усложнять модель с учетом коэффициента перемешивания, либо усложнять модель с учетом гидродинамики потоков в аппарате. Это может быть не оправдано по удельным затратам времени на разработку модели, а при неполном учете в модели всех протекающих физико-химических явлений приводить к значительным ошибкам.
2) Процесс смешения – адиабатический, не учитывается теплота смешения;
В противном случае необходимо учитывать процессы подвода и отвода теплоты, а также теплоту смешения, выделяющуюся при смешении веществ (в особых случаях, в тепловом балансе смесителя требуется учитывать теплоту смешения).
3) Все потоки имеют одно фазовое состояние;
В противном случае модель нужно будет значительно усложнить, т.к. необходимо использовать смеситель, имеющий 2 или 3 выходных потока (газ, жидкость и твердое), т.к. одним потоком невозможно одновременно выразить различные фазовые состояния, будет необходимо учитывать фазовое равновесие в системе твердое-жидкость-газ, и условия его установления, а также тепловой баланс процессов установления фазового равновесия.
4) Давление входных и выходных потоков – одинаковое;
При изменении давления могут возникнуть условия, приводящие к изменению фазового состояния (см.выше).
При соблюдении всех указанных выше допущений рассмотрим уравнения, входящие в основу математического описания модели смесителя.
Общее уравнение материального баланса запишется:
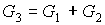 [4.2]
[4.2]
С использованием уравнения материального баланса для вещества можно рассчитать состав выходного потока:
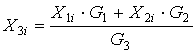 , при i=1…k [4.3]
, при i=1…k [4.3]
При составлении материального баланса особое внимание требуется обратить на единицы измерения расходов и составов. Обычно рекомендуется использовать мольный расход [моль/сек] и состав [%мольн.] или массовый расход [кг/сек] и состав [%масс.] или, при смешении газовых потоков, объемный расход при нормальных термодинамических условиях (0ОС и 1 атм), т.е. [нм3/сек], и объемный состав [%об.].
Следует отметить, что при расчетах состав потока обычно используется не в процентах, а в долях (сумма = 1), а использование различных единиц измерения для расхода и состава недопустимо.
Общее уравнение теплового баланса запишется:
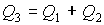 [4.4]
[4.4]
При неизвестной теплоте потока, она может быть рассчитана на основании материального баланса по уравнению:
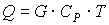 [4.5]
[4.5]
где СР – удельная изобарная теплоемкость потока (смеси веществ), которая рассчитывается по правилу аддитивности:
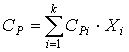 [4.6]
[4.6]
где СРi – изобарная теплоемкость i-го компонента потока, которая может быть рассчитана по уравнению:
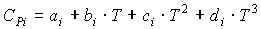 [4.7]
[4.7]
коэффициенты a, b, c и d которого для i-го вещества берутся из справочника.
Температура выходного потока рассчитывается методом итераций:
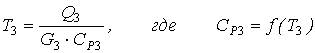 [4.8]
[4.8]
Модуль делителя:
Модуль делителя является одним из наиболее простых модулей. В соответствии с исходной задачей, поток вещества, имеющий расход G1 (моль/сек), температуру T1 (град.К), составы X1i (мольные доли) и теплоту Q1 (Вт) подается в делитель, откуда выходят два потока с расходами G2 иG3, температурами T2 и T3, составами X2i и Х3i и теплотой Q2 и Q3(см.Рис.4.12).
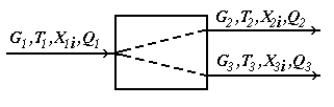
Рис.4.12. Схема модуля делителя
Физико-химическая модель делителя предназначена для расчета материального и теплового балансов процесса деления одного потока вещества на два потока. Существуют модули для деления потока на большее количество потоков, но они являются расширенной модификацией делителя на два потока.
Для делителя, допущения будут следующие:
1) Состав, температура и давление выходных потоков равны составу, температуре и давлению входного потока;
2) Все потоки имеют одно фазовое состояние.
Известно два способа деления потока. Для ПЕРВОГО способа требуется знать расход первого выходящего потока, а для ВТОРОГО – коэффициент деления потока. В зависимости от типа связанного с делителем оборудования, применяться могут оба способа, однако ПЕРВЫЙ способ имеет ограничения, которые заключаются в том, что используются абсолютные значения, а не относительные. Например, в процессе расчетов, расход входящего потока будет меньше заданного расхода первого выходящего потока, т.е. второй выходящий поток будет иметь отрицательный расход, что невозможно. ВТОРОЙ способ более стабильный в расчетах, т.к. используются относительные значения, однако, в зависимости от типа связанного с делителем оборудования, использование фиксированного коэффициента деления может не соответствовать реальной ХТС.
Для реализации ПЕРВОГО способа необходимо знать: расход G1 (моль/сек), температура T1 (град.К), состав X1i (мольные доли) и теплота Q1 (Вт), также расход первого выходящего потока G2.
Основное уравнение материального баланса запишется:
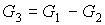 [4.9]
[4.9]
Исходя из допущения, состав выходных потоков будет равен составу входного потока:
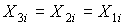 , при i=1…k [4.10]
, при i=1…k [4.10]
Теплоты выходящих потоков могут быть рассчитаны пропорционально расходам выходящих потоков (температура и состав выходящих потоков равны входящему) или рассчитаны на основании материального баланса по уравнению:
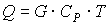 [4.11]
[4.11]
где СР – удельная изобарная теплоемкость потока (смеси веществ), которая рассчитывается по правилу аддитивности:
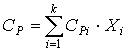 [4.12]
[4.12]
где СРi – изобарная теплоемкость i-го компонента потока, которая может быть рассчитана по уравнению:
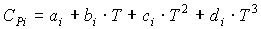 [4.13]
[4.13]
коэффициенты a, b, c и d которого для i-го вещества берутся из справочника.
Для реализации ВТОРОГО способа расчета должны быть известны: расход G1 (моль/сек), температура T1 (град.К), состав X1i (мольные доли) и теплота Q1 (Вт), также задан коэффициент деления входящего потока Kf (в соответствии с обозначениями на Рис.4.3, Kf = G2/G1).
В данном случае расходы выходящих из делителя потоков могут быть рассчитаны по формулам:
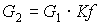 [4.14]
[4.14]
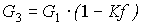 [4.15]
[4.15]
Далее, алгоритм расчета не отличается от алгоритма ПЕРВОГО способа расчета, приведенного выше.
Модуль теплообменника:
В отличие от модулей смесителя и делителя, модуль теплообменника не является столь простым, т.к. при изменении температуры потоков возможно изменение их фазового состояния, а, следовательно, при расчете необходимо учитывать такие изменения. В связи с этим, например, только для систем газ-газ, жидкость-жидкость и газ-жидкость различают следующие модели теплообменников:
1) Теплообменник газ-газ или жидкость-жидкость без фазовых переходов (нагреватели и холодильники);
2) Теплообменник газ-газ или жидкость-жидкость с фазовым переходом (для системы газ-газ он называется конденсатор, а для системы жидкость-жидкость – испаритель, также существует более сложный вариант, когда тепло от конденсирующегося газа используется для испарения жидкости);
Кроме того, так как на процесс расчета теплообменника оказывает влияние его конструкция, то для каждого указанного выше типа теплообменников различают следующие модели:
1) Противоточный ("холодный" и "горячий" агенты идут навстречу друг другу, т.е. противотоком);
2) Прямоточный ("холодный" и "горячий" агенты идут параллельно, т.е. прямотоком);
3) Перекрестноточный (промежуточный вариант между указанными выше);
4) Одноходовой или многоходовой теплообменники (в многоходовых теплообменниках часть труб работает в режиме противотока, а часть – в режиме прямотока, или в многоходовом перекрестноточном теплообменнике жидкость или газ по трубам может двигаться по ходу или против хода потока в межтрубном пространстве);
5) Варианты, когда один из агентов (или оба агента) движется за счет естественной конвекции, которые, по интенсивности перемешивания потока за счет естественной конвекции, в свою очередь делятся на горизонтальные и вертикальные;
6) Теплообменники смешения ("холодный" и "горячий" агенты непосредственно контактируют друг с другом, например, в аппарате с насадкой).
И, наконец, теплообменники, различающиеся по режиму работы на:
1) периодические;
2) непрерывные.
Следует отметить, что согласно исходной задачи для модуля ХТС, требуется рассчитать параметры выходных потоков при известных параметрах входных потоков и параметров элемента ХТС (в случае теплообменника, при известной площади теплообмена и коэффициента теплопередачи), что соответствует проверочному расчету теплообменника. Однако иногда возникает необходимость рассчитать размеры теплообменника, входящего в ХТС. В таком случае необходимо использовать проектный расчет теплообменника.
В качестве примера рассмотрим проверочный расчет теплообменника-подогревателя для системы газ-газ, жидкость-жидкость или газ-жидкость с учетом следующих допущений:
- Одноходовой кожухотрубный теплообменник в стационарном режиме;
- Теплопередача не сопровождается изменением агрегатного состояния;
- Коэффициенты теплоотдачи для "холодного" и "горячего" потоков рассчитывается при начальных температурах теплоносителей;
- Схема движения потоков – противоточная;
- Потери теплоты отсутствуют.
Схема теплообменника представлена на Рис.4.13.
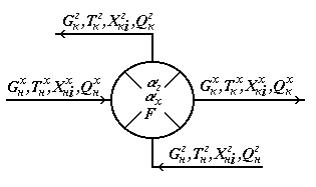
Рис.4.13. Схема теплообменника
В соответствии с исходной задачей, для входного "горячего" потока известен расход GГН, температура ТГН, состав ХГН и теплота QГН., для входного "холодного" потока – расход GХН, температура ТХН, состав ХХН и теплота QХН. Кроме параметров потока, для теплообменника известны коэффициенты теплоотдачи для "холодного" и "горячего" потоков aХ и aГ, и площадь теплопередачи F.
В связи с тем, что фазового перехода не происходит, материальный баланс теплообменника запишется равенствами расходов и составов выходных потоков входным:
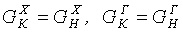 [4.16]
[4.16]
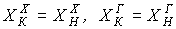 [4.17]
[4.17]
В соответствии с тепловым балансом:
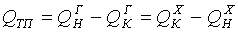 [4.18]
[4.18]
или
 [4.19]
[4.19]
где, коэффициент теплопередачи:
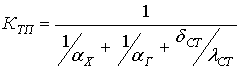 [4.20]
[4.20]
где, dСТ и lСТ – толщина и теплопроводность стенки
"движущая сила" теплопередачи:
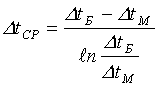 [4.21]
[4.21]
где DtБ и DtМ – большая и меньшая разности температур на входах и выходов теплообменника с учетом взаимного хода потоков, например, для противотока:
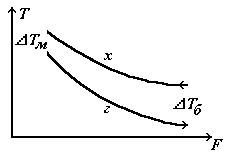
т.е. DtБ = большее из (ТГН - ТГК), ( ТХК - ТХН) [4.22]
DtМ = меньшее из (ТГН - ТГК), ( ТХК - ТХН) [4.23]
Так как температуры "горячего" и "холодного" потоков на выходе теплообменника неизвестны, то провести простой расчет не представляется возможным, поэтому, можно рекомендовать проведение расчета методом перебора или минимизации в соответствии со следующим алгоритмом:
1. Задается некоторое первоначальное значение температуры "холодного" потока на выходе из теплообменника. Обычно: ТХК = ТХН+0,1;
2. При известной температуре "холодного" потока на выходе, его составе и расходе, по формуле [4.11] с учетом формул [4.12 и 4.13] рассчитывается его теплосодержание QХК;
3. С использованием формулы теплового баланса [4.18] рассчитывается тепловая нагрузка на теплообменник QТП и теплосодержание выходного "горячего" потока QГК;
4. По величине теплосодержания выходного "горячего" потока QГК определяется его температура (см. [4.7]) и движущая сила теплопередачи [4.21];
5. Определяется разность теплоты теплопередачи, рассчитанной в п.3 и по формуле основного уравнения теплопередачи [4.19];
6. Если разность, определенная в п.5, меньше заданной точности расчета, то расчет заканчивается. В противном случае температура выходящего "холодного" потока увеличивается на некоторое значение, и расчет повторяется с п.2.
При использовании математических методов минимизации, в п.4 необходимо добавить логические условия по анализу пересечения линий нагревания/охлаждения, т.е. чтобы температура "холодного" потока на входе и выходе теплообменника не была выше температуры "горячего" потока.
В заключение следует отметить, что кроме указанного алгоритма поверочного расчета теплообменника, существуют другие алгоритмы, приводящие к аналогичным результатам.
Из всего разнообразия теплообменного оборудования, исходя из начальных условий, выше был рассмотрен простейший вариант одноходового противоточного кожухотрубного теплообменника-подогревателя без учета фазовых переходов и потерь. При возникновении фазовых переходов расчет значительно усложняется, т.к. в данном случае требуется не только учитывать в тепловом балансе теплоту фазовых переходов, их полноту и "излом" линий нагрева/охлаждения, но и пересчитывать материальный баланс с учетом фазового равновесия и изменения состава и массы потоков вследствие фазовых переходов. Несомненно, данная задача является достаточно сложной и не универсальной, т.к. требует создания алгоритмов расчета для каждого конкретного случая.
Кроме рассмотренного выше интегрального подхода к расчету теплообменника, существует и дифференциальный подход, заключающийся в интегрировании дифференциальных уравнений материального и теплового баланса теплообменника по площади теплообмена с учетом всех нюансов. Основным преимуществом дифференциального подхода является отсутствие сложных методов учета всех особенностей теплопередачи для всего теплообменника и его универсальность, т.к. различные особенности теплообмена всегда учитываются в дифференциальных уравнениях для элементарной площади теплопередачи dF. Именно поэтому, данный подход используется большинством программных продуктов для расчета ХТС, речь о которых пойдет в последних главах.
В связи с относительно высокой сложностью алгоритмов расчета теплообменников с учетом фазовых переходов, модулей реакторов, модулей фазового равновесия, межфазного массообмена и т.д., в настоящем конспекте лекций они не приводятся. Полное описание алгоритмов расчета этих модулей, а также дополнительные алгоритмы расчета смесителя, делителя и теплообменника, можно найти в литературе по моделированию химико-технологических процессов.


