1.2. Зависимость поверхностного натяжения жидкостей от температуры
Как известно, с увеличением температуры интенсивность межмолекулярного взаимодействия уменьшается, поэтому снижается и поверхностное натяжение жидкостей на границе с воздухом или с собственным паром. Вдали от критической температурыповерхностное натяжение уменьшается прямо пропорционально росту температуры. Эту зависимость обычно описывают эмпирическим уравнением
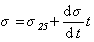 1 1.11
1 1.11
где s25 – поверхностное натяжение при температуре 25оС.
Температурный коэффициент поверхностного натяжения, имеющий отрицательное значение, остается постоянным вдали от критической температуры. При температуре, близкой к критической, поверхностное натяжение резко снижается вплоть до нуля. Следует отметить, что такая зависимость справедлива только для чистых жидкостей, тогда как для растворов наряду с изменением поверхностного натяжения возможно изменение концентрации растворенного вещества в поверхностном слое, что приведет к вторичным эффектам, способным вызвать повышение поверхностного натяжения. Полная внутренняя энергия при изменении температуры вдали от критической остается практически неизменной (изменяется лишь при температуре, близкой к температуре исчезновения поверхности раздела фаз).
Эмпирическое уравнение, устанавливающее зависимость поверхностного натяжения от температуры, предложил Этвеш. Интегральная форма этого уравнения имеет вид
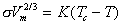 , (1.1.14)
, (1.1.14)где Vm- молярный объем жидкости; K- постоянная; Tс- критическая температура.
Учитывая предложенное Ван-дер-Ваальсом уравнение
 , (1.1.15)
, (1.1.15)
где n=11/9 для многих органических жидкостей, n=1 для металлов; s0 – гипотетическое поверхностное натяжение при температуре 0 K; для постоянной K уравнения (1.1.14) получаем выражение
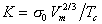 . (1.1.16)
. (1.1.16)
Уравнения (1.1.15) и (1.1.16) достаточно корректны для неполярных жидкостей, а для воды дают большую погрешность. Из уравнения (1.1.16) следует размерность постоянной K [Дж/град·моль2/3], что не имеет физического смысла. Если относить эту постоянную к одной молекуле, то для большинства жидкостей получается величина, соответствующая постоянной Больцмана 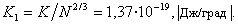 Из этого следует, что уравнение Этвеша достаточно строго можно вывести из статистико-механической теории жидкостей.
Из этого следует, что уравнение Этвеша достаточно строго можно вывести из статистико-механической теории жидкостей.
Строгое уравнение зависимости поверхностного натяжения от температуры можно получить из уравнения Гиббса-Гельмгольца
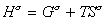 , (1.1.17) где индекс s указывает на отнесение энтальпии энергии Гиббса и энтропии к единице площади поверхности. Часто энтальпия и полная внутренняя энергия поверхности неразличимы и могут хорошо аппроксимировать друг друга. Поэтому уравнение (1.1.17) можно записать
, (1.1.17) где индекс s указывает на отнесение энтальпии энергии Гиббса и энтропии к единице площади поверхности. Часто энтальпия и полная внутренняя энергия поверхности неразличимы и могут хорошо аппроксимировать друг друга. Поэтому уравнение (1.1.17) можно записать 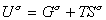 , (1.1.18)
, (1.1.18)или, учитывая, что для единицы площади поверхности Gs=s, запишем
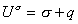 , (1.1.19) где
, (1.1.19) где 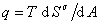 . Учитывая, что
. Учитывая, что  , (1.1.20)
, (1.1.20)можем записать для единицыплощади поверхности
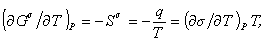 (1.1.21)
(1.1.21)
поэтому
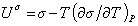 , (1.1.22)
, (1.1.22)
или
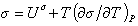 . (1.1.23)
. (1.1.23)
Уравнение (1.1.23) описывает зависимость поверхностного натяжения от температуры. Уравнение (1.1.22) может быть также записано в виде
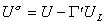 , (1.1.24)
, (1.1.24)
где U - внутренняя энергия молекул на единице площади поверхности; UL- внутренняя энергия молекулы в объеме жидкости; 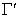 - общее число молекул на единице площади поверхности.
- общее число молекул на единице площади поверхности.
Уравнение (1.1.24) известно как уравнение Гугенгейма-Гудриха.
Зная температурный коэффициент поверхностного натяжения, можно рассчитать внутреннюю энергию поверхности. Для многих неполярных жидкостей энергия Us остается постоянной и в широкой области температуры вплоть до критической, вблизи которой как s, так и Us резко уменьшаются вплоть до нуля.
Действительно, независимость Us от температуры становится очевидной, если продифференцировать по температуре уравнение Гиббса-Гельмгольца для поверхностного слоя:
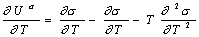 . (1.1.25)
. (1.1.25)
Поскольку для многих жидкостей первая производная поверхностного натяжения по температуре имеет постоянную величину в широкой области температуры и лишь вблизи критической температуры теряет это свойство, то
|
 , (1.1.26)
, (1.1.26)
поэтому
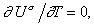 (1.1.27)
(1.1.27)
т.е.
Us= const
|
На рис. 1.3 приведена зависимость внутренней энергии поверхности и поверхностного натяжения от температуры.
При критической температуре, когда свойства пара и жидкости становятся одинаковыми и исчезает поверхность раздела фаз, все энергетические поверхностные характеристики системы стремятся к нулю, как это показано на рис. 1.3.

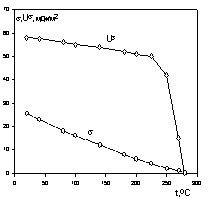 Рис. 1.3. Зависимость энергетических параметров поверхности от температуры
Рис. 1.3. Зависимость энергетических параметров поверхности от температуры Рис. 1.4. Схема изменения объема пузырька
Рис. 1.4. Схема изменения объема пузырька 
