Ван-дер-Ваальса уравнение

ВАН-ДЕР-ВААЛЬСА УРАВНЕНИЕ, ур-ние состояния реального газа. Для п молей газа, имеющего объем V при т-ре Т и давлении р. имеет вид: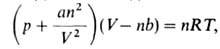

где R-газовая постоянная, а и b-постоянные Ван-дер-Ваальса, характерные для данного в-ва. Член an²/V² учитывает притяжение молекул газа (уменьшение давления) вследствие межмолекулярных взаимод., член nb-отталкивание молекул на близких расстояниях из-за наличия у них "собственного объема". Для разреженных газов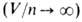 Ван-дер-Ваальса уравнение принимает вид: pV = nRT (см. Клапейрона-Менделеева уравнение). Постоянные а и b определяют экспериментально, напр. по параметрам критич. точки.

Ван-дер-Ваальса уравнение - простейшее ур-ние состояния, позволяющее определять точку фазового перехода газ - жидкость и критич. т-ру, выше к-рой в-во может находиться только в газообразном состоянии. Однако Ван-дер-Ваальса уравнение является приближенным и количественно описывает нек-рые св-ва газа лишь при высоких Т и низких р. Оно даже качественно не описывает многие св-ва реального газа, напр. зависимость изохорной теплоемкости от плотности. Термодинамич. св-ва газов м. б. рассчитаны с достаточной точностью на основе вириаль-ного уравнения состояния.

Ур-ние было предложено И. Д. Ван-дер-Ваальсом в 1873.

Лит. см. при ст. Газы. М.А. Анисимов.

Комментарии^*

Дополнения к описанию уравнения Ван-дер-Ваальса:

Структура уравнения: (p + an²/V²)(V - nb) = nRT
Физическая интерпретация постоянных:
- Постоянная a характеризует силу притяжения между молекулами
- Постоянная b соответствует объему, исключенному из-за конечного размера молекул
Критическая точка: Уравнение предсказывает существование критической точки с параметрами:
- Критический объем: Vк = 3nb
- Критическое давление: pк = a/(27b²)
- Критическая температура: Tк = 8a/(27Rb)
Значение в истории науки: Это была первая успешная попытка модифицировать уравнение состояния идеального газа с учетом межмолекулярных взаимодействий
Диаграммы состояния: Уравнение описывает изотермы, показывающие переход между газообразной и жидкой фазами
Современное применение: Хотя уравнение имеет ограничения, оно остается важным учебным инструментом для понимания поведения реальных газов и фазовых переходов