3.2.1. Модель монослоя
Основоположником мономолекулярной модели физической адсорбции был Ленгмюр. В соответствии с развитыми им представлениями адсорбционный слой состоит из локализованных на экспотенциальной поверхности не взаимодействующих друг с другом молекул (отсутствуют латеральные – боковые - взаимодействия).
При равновесном давлении Р и постоянной температуре T количествоадсорбированных молекул (на единице площади адсорбента) выражается числом молей n s или молекул N s в адсорбционном слое:
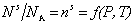 , (1.3.4)
, (1.3.4)
где NA – Число Авогадро.
Такую зависимость называют изотермой адсорбции.
Часто адсорбцию выражают через эквивалентный для nsмолей адсорбата объем при нормальных температуре и давлении V s (см3). Поэтому изотерма адсорбции может быть выражена как
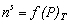 или
или 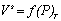 . (1.3.5)
. (1.3.5)
Для описания мономолекулярного при малых степенях заполнения адсорбционного слоя прибегают к модели двумерного газа, а при насыщении адсорбционного слоя считают его двумерной жидкостью. В таком случае для ненасыщенного слоя адсорбата полагается справедливым уравнение состояния двумерного газа
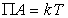 , (1.3.6)
, (1.3.6)
где 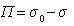 – поверхностное давление;
– поверхностное давление; 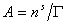 – площадь, занимаемая одним молем адсорбированного вещества; Г – гиббсовская адсорбция (поверхностный избыток); s0, s – поверхностное натяжение на межфазной границе до и после адсорбции, соответственно.
– площадь, занимаемая одним молем адсорбированного вещества; Г – гиббсовская адсорбция (поверхностный избыток); s0, s – поверхностное натяжение на межфазной границе до и после адсорбции, соответственно.
Записывая уравнение Гиббса
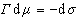 (1.3.7)
(1.3.7)
и вводя замену 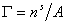 , получаем
, получаем
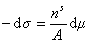 . (1.3.8)
. (1.3.8)
Введем степень заполнения адсорбционного слоя
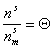 , (1.3.9)
, (1.3.9)
где 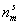 – предельное количество адсорбата при насыщении адсорбционного слоя.
– предельное количество адсорбата при насыщении адсорбционного слоя.
Домножая числитель и знаменатель правой части уравнения (1.3.8) на 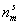 , получаем
, получаем
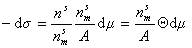 . (1.3.10)
. (1.3.10)
Химические потенциалы молекул в адсорбционном слое и в равновесной газовой фазе должны быть равны, поэтому
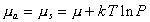 и
и 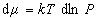 . (1.3.11)
. (1.3.11)
Поэтому
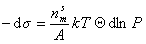 . (1.3.12)
. (1.3.12)
Интегрируя уравнение (1.3.12) при условии, что при P=0 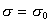 , учитывая, что П=s0 - s , и обозначая Аm=А/nsm
, учитывая, что П=s0 - s , и обозначая Аm=А/nsm
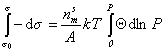 , (1.3.13)
, (1.3.13)
получаем
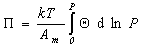 . (1.3.14)
. (1.3.14)
Уравнение состояния двумерного идеального газа (1.3.6) можем переписать в виде
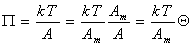 . (1.3.15)
. (1.3.15)
Дифференцируя и сопоставляя уравнения (1.3.14) и (1.3.15), получаем
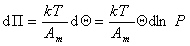 (1.3.16)
(1.3.16)
или 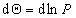 , откуда
, откуда
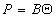 , (1.3.17)
, (1.3.17)
где B – постоянная. Уравнение (1.3.17) известно как уравнение Генри. Учет собственных размеров молекул адсорбата А0 в уравнении состояния двумерного газа проводится как
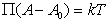 . (1.3.18)
. (1.3.18)
В общем случае уравнение состояния двумерного газа может быть записано в виде
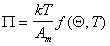 . (1.3.19)
. (1.3.19)
Использование описанного выше при выводе уравнения Генри подхода дает обобщенную функцию идеальной модельной изотермы, которая выражается уравнением Ленгмюра
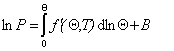 , (1.3.20)
, (1.3.20)
или
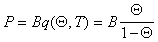 . (1.3.21)
. (1.3.21)
Учитывая уравнение (1.3.18), использование указанного выше подхода приводит к уравнению Фольмера
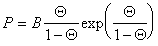 . (1.3.22)
. (1.3.22)
Введение двумерного аналога уравнения Ван-дер-Ваальса
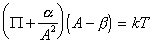 , (1.3.23)
, (1.3.23)
где a и b – постоянные, дает изотерму адсорбции, известную как уравнение Хилла-де-Бура
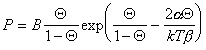 . (1.3.24)
. (1.3.24)
Приведенное выше уравнение (1.3.21) Ленгмюр вывел на основании рассмотрения динамического равновесия между адсорбционным слоем и объемом газовой фазы.
Из кинетической теории газов следует, что число молекул газа, сталкивающихся за единицу времени с единицей площади адсорбента (диффузионный поток), будет
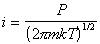 . (1.3.25)
. (1.3.25)
Учитывая, что адсорбция не может происходить, если молекула контактирует с уже занятым активным центром, из диффузионного потока будет захвачена адсорбентом лишь часть молекул j, остальные молекулы будут отражены. Если доля занятых активных центров будет Q, то скорость адсорбции можно выразить как
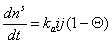 . (1.3.26)
. (1.3.26)
Скорость десорбции будет
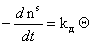 . (1.3.27)
. (1.3.27)
При равновесии
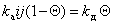 , (1.3.28)
, (1.3.28)
где kа и kд – постоянные скорости процессов адсорбции и десорбции.
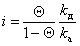 . (1.3.29)
. (1.3.29)
Подставляя в уравнение (1.3.29) выражение для i из (1.3.25), получаем
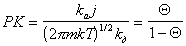 , (1.3.30)
, (1.3.30)
откуда
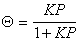 ,
, (1.3.31)
(1.3.31)
или
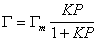 , (1.3.32)
, (1.3.32)
где K – постоянная равновесия процесса адсорбции,Q =Г/Гm.
Сопоставление уравнений (1.3.30) и (1.3.21) показывает, что постоянная интегрирования обратна величине постоянной равновесия адсорбции, т.е. В = 1/K.
Уравнение Ленгмюра справедливо лишь для идеального локализованного монослоя, исключающего латеральные взаимодействия между молекулами, адсорбированными на соседних центрах.
Очевидно, что такое взаимодействие в реальных системах должно проявляться и статистико-термодинамическое рассмотрение приводит к уравнению Фаулера-Гугенгейма
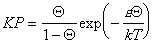 , (1.3.33)
, (1.3.33)
где e – энергия латерального взаимодействия.
Уравнение (1.3.33) дает изотермы, практически идентичные с уравнением (1.3.24) Хилла-де-Бура. Существуют определенные критические условия, при которых начинает проявляться латеральное взаимодействие, т.е. происходит двумерная конденсация и уравнение Ленгмюра становится неприменимым. В случае изотермы Фаулера-Гугенгейма критическим условиям соответствуют КР = 0,1353 и Q = 0,5; e/kT= 4.
Все приведенные выше изотермы адсорбции, основанные на мономолекулярной модели адсорбционного слоя предполагают экспотенциальность поверхности, которая считается однородной. В реальных системах поверхности неоднородны, особенно это проявляется у волокон полимерных материалов.


