1.3.1. Уравнение Лапласа
Рассмотрим сферический пузырек воздуха радиуса r в среде жидкости. Если увеличить размер пузырька, например при введении некоторого количества газа, как это показано на рис. 1.4, то увеличится поверхность пузырька, а затраченная на это увеличение работа может быть выражена как работа на преодоление сил поверхностного натяжения или как работа увеличения объема пузырька на преодоление внутреннего давления в жидкости Pk. Учитывая, что давление в пузырьке должно быть больше давления в жидкости, можем записать
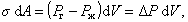 (1.1.28)
(1.1.28)
где Pг - давление газа в пузырьке.
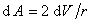 , (1.1.29)
, (1.1.29)
поэтому
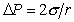 , (1.1.30)
, (1.1.30)
т.е. разность давлений в соседних фазах, разделенных искривленной поверхностью, определяется радиусом кривизны поверхности.
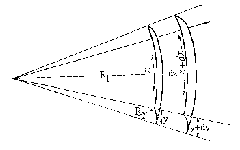
Рис. 1.5. Схема изменения мениска произвольной формы |
Рассмотрим расширение некоторой фигуры произвольной кривизны, схема небольшого участка поверхности (мениска) которой приведена на рис. 1.5. Кривизна этой поверхности выражается двумя радиусами R1 и R2. Один из этих радиусов (R1) лежит в плоскости рисунка, а другой (R2)– в перпендикулярной плоскости. Если выбранный участок поверхности достаточно мал, то R1 и R2 можно считать постоянными. Если поверхность сместить на некоторую бесконечно малую величину dz, то площадь изменится на величину
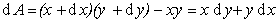 , (1.1.31)
, (1.1.31)
а объем на величину
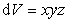 . (1.1.32)
. (1.1.32)
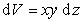 . (1.1.32)
. (1.1.32)
Из подобия треугольников, приведенных на рис. 1.5., следует, что
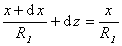 или
или 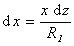 ; (1.1.33)
; (1.1.33)
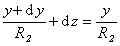 или
или 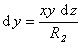 . (1.1.34)
. (1.1.34)
Так как при равновесии системы работа увеличения поверхности будет равна работе увеличения объема, то
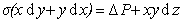
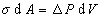 . (1.1.36) Поэтому с учетом уравнений (1.1.33) и (1.1.34)
. (1.1.36) Поэтому с учетом уравнений (1.1.33) и (1.1.34) 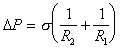 . (1.1.37)
. (1.1.37)Уравнение (1.1.37) представляет собой основное уравнение теории капиллярных явлений и также как уравнение (1.1.30) носит название «уравнение Лапласа».