1.3.2. Сферические мениски
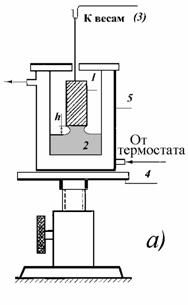
Наиболее простой случай проявления капиллярности возможен при образовании мениска в капилляре круглого сечения с небольшим радиусом в приборе для определения поверхностного натяжения, схема которого приведена на рис. 1.6,а. В этом случае оба радиуса кривизны равны радиусу капилляра и уравнение Лапласа (1.1.37) записывают в виде
ΔР=2σ/r=2σ cosΘ/r0, (1.1.38)
где r0 – радиус капилляра, r – радиус кривизны мениска, r = r0cosQ, Q - угол смачивания стенки капилляра жидкостью.
В случае полного смачивания стенки жидкостью, когда Q=0, а cosQ =1, используют уравнение
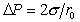 . (1.1.39)
. (1.1.39)
Обозначим высоту мениска в капилляре над плоской поверхностью h. Нулевым считается уровень, для которого 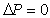 . Объемом жидкости в мениске (т.е. выше h) пренебрегают. Очевидно, что в равновесном состоянии капиллярное давление уравновешивается гидростатическим:
. Объемом жидкости в мениске (т.е. выше h) пренебрегают. Очевидно, что в равновесном состоянии капиллярное давление уравновешивается гидростатическим:
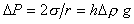 , (1.1.40)
, (1.1.40)где Dr – разность плотностей жидкости и газа.
Из этого уравнения
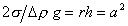 , (1.1.41)
, (1.1.41)
где a – капиллярная постоянная.
Уравнение (1.1.40) лежит в основе определения поверхностного натяжения методом капиллярного поднятия. Это уравнение не учитывает объема жидкости в мениске, поэтому оно считается достаточно корректным только для тонких капилляров (диаметром менее 1 мм), в которых r/h=2·10-2.
Для более точного расчета поверхностного натяжения необходимо учитывать массу жидкости в мениске. Существуют различные поправки, учитывающие также и отклонение формы мениска от сферической. Все эти поправки справедливы только при полном смачивании, т. е. приQ=0.
Одной из первых была предложена поправка для учета количества жидкости в сферическом мениске путем введения дополнительного слагаемого в уравнение (1.1.41):
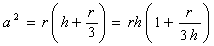 . (1.1.42)
. (1.1.42)
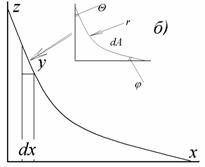
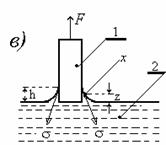
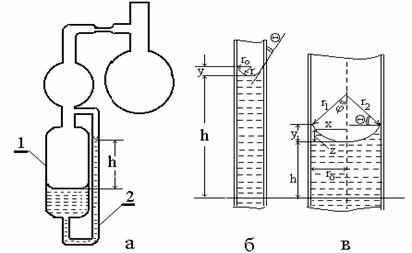
Отклонение формы мениска от сферической можно учитывать с помощью уравнения Рэлея, справедливого при r< Рис. 1.6. Схема прибора для определения поверхностного натяжения методом капиллярного поднятия (a), мениск жидкости в узком (б) и в широком (в) капиллярах Первый член разложения соответствует простому уравнению (1.1.41), второй - учитывает массу жидкости в мениске, форма которого предполагается сферической, а третий - отклонение формы мениска от сферической. Хаган и Дизайненс при решении задачи для эллиптического мениска пришли к аналогичному уравнению: Для узких трубок поправки, рассчитанные по уравнениям (1.1.42), (1.1.43) и (1.1.44), соответственно составляют 1,005; 1,006617 и 1,006623, что коррелирует с погрешностью определения h порядка 10-6м. Решение задачи введения поправок на отклонение от сферичности для широких капилляров привело Рэлея к выводу, что для воды необходима трубка с диаметром 5 см, чтобы исключить капиллярное поднятие. Для капилляров промежуточного размера используют поправки Бешфорта и Адамса. Если рассматривать фигуру вращения, приведенную на рис. 1.6, в, в точке пересечения мениска с его осью, т.е. при капиллярном поднятии на его дне, то оба радиуса кривизны должны быть равны (r1=r2). Обозначим в точке z r1=r2=b. Тогда При z=0 DP=2s/b, а при любом другом значении z изменение давления DP=Dgz. Бешфорт и Адамс для расчета поправок предложили использовать уравнения в безразмерной форме: где j - угол, дополняющий угол смачивания до 90o. Числовые решения уравнения (1.1.46) были проведены Бешфортом и Адамсом и приведены в виде таблиц для различных b и j. Эти таблицы позволяют внести поправки при расчете поверхностного натяжения по экспериментально измеренным радиусам капилляров, плотности жидкостей и воздуха, высоте подъема жидкостей по капиллярам и уточнить значения радиуса кривизны мениска и поверхности натяжения. Рис.1.7. Схема прибора для определения поверхностного натяжения методом Вильгельми (а), схема цилиндрического мениска у вертикальной пластинки (б), пластинка, подвешенная в жидкости (в).
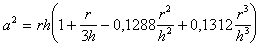 . (1.1.43)
. (1.1.43)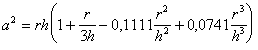 . (1.1.44)
. (1.1.44)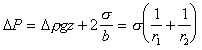 . (1.1.45)
. (1.1.45)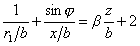 , (1.1.46)
, (1.1.46) 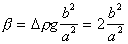 , (1.1.47)
, (1.1.47)