Капиллярные явления
КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ, поверхностные явления на границе жидкости с др. средой, связанные с искривлением ее пов-сти. Искривление пов-сти жидкости на границе с газовой фазой происходит в результате действия поверхностного натяжения жидкости, к-рое стремится сократить пов-сть раздела и придать ограниченному объему жидкости форму шара. Поскольку шар обладает миним. пов-стью при данном объеме, такая форма отвечает минимуму поверхностной энергии жидкости, т.е. ее устойчивому равновесному состоянию. В случае достаточно больших масс жидкости действие поверхностного натяжения компенсируется силой тяжести, поэтому маловязкая жидкость быстро принимает форму сосуда, в к-рый она налита, а ее своб. пов-сть представляется практически плоской. В отсутствие силы тяжести или в случае очень малых масс жидкость всегда принимает сферич. форму (капля), кривизна пов-сти к-рой определяет мн. св-ва в-ва. Поэтому капиллярные явления ярко выражены и играют существ. роль в условиях невесомости, при дроблении жидкости в газовой среде (или распылении газа в жидкости) и образовании систем, состоящих из мн. капель или пузырьков (эмульсий, аэрозолей, пен), при зарождении новой фазы капель жидкости при конденсации паров, пузырьков пара при вскипании, зародышей кристаллизации. При контакте жидкости с конденсир. телами (др. жидкостью или твердым телом) искривление пов-сти раздела происходит в результате действия межфазного натяжения. В случае смачивания, напр., при соприкосновении жидкости с твердой стенкой сосуда, силы притяжения, действующие между молекулами твердого тела и жидкости, заставляют ее подниматься по стенке сосуда, вследствие чего примыкающий к стенке участок пов-сти жидкости принимает вогнутую форму. В узких каналах, напр., цилиндрич. капиллярах, образуется вогнутый мениск - полностью искривленная пов-сть жидкости (рис. 1).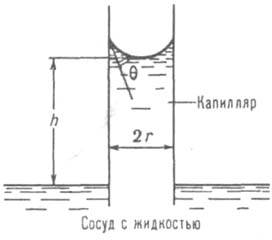
Рис. 1. Капиллярное поднятие на высоту h жидкости, смачивающей стенки капилляра радиуса r; q - краевой угол смачивания.
Капиллярное давление. Т. к. силы поверхностного (межфазного) натяжения направлены по касательной к пов-сти жидкости, искривление последней ведет к появлению составляющей, направленной внутрь объема жидкости. В результате возникает капиллярное давление, величина к-рого Dp связана со средним радиусом кривизны пов-сти r0 ур-нием Лапласа:
Dp = p1 - p2 = 2s12/r0, (1)
где p1 и p2 - давления в жидкости 1 и соседней фазе 2 (газе или жидкости), s12 - поверхностное (межфазное) натяжение. Если пов-сть жидкости вогнута (r0<0), давление в ней оказывается пониженным по сравнению с давлением в соседней фазе p1 < р2 и Dp < 0. Для выпуклых пов-стей (r0 > 0) знак Dp изменяется на обратный. Отрицат. капиллярное
давление, возникающее в случае смачивания жидкостью стенок капилляра, приводит к тому, что жидкость будет всасываться в капилляр до тех пор, пока вес столба жидкости высотой h не уравновесит перепад давления Dp. В состоянии равновесия высота капиллярного поднятия определяется ф-лой Жюрена:
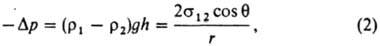
где r1 и r2 - плотности жидкости 1 и среды 2, g - ускорение силы тяжести, r - радиус капилляра, q - краевой угол смачивания. Для несмачивающих стенки капилляра жидкостей cos q < 0, что приводит к опусканию жидкости в капилляре ниже уровня плоской пов-сти (h < 0).
Из выражения (2) следует определение капиллярной постоянной жидкости а = [2s12/(r1 — r2)g]1/2. Она имеет размерность длины и характеризует линейный размер Z [ а, при к-ром становятся существенными капиллярные явления. Так, для воды при 20 °С а = 0,38 см. При слабой гравитации (g : 0) значение а возрастает. На участке контакта частиц капиллярная конденсация приводит к стягиванию частиц под действием пониж. давления Dp < 0.
Уравнение Кельвина. Искривление пов-сти жидкости приводит к изменению над ней равновесного давления пара р по сравнению с давлением насыщ. пара ps над плоской пов-стью при той же т-ре Т. Эти изменения описываются ур-нием Кельвина:
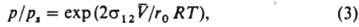
где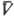 
- молярный объем жидкости, R - газовая постоянная. Понижение или повышение давления пара зависит от знака кривизны пов-сти: над выпуклыми пов-стями (r0 > 0) p > ps; над вогнутыми (r0 < 0) р < рs. Так, над каплями давление пара повышено; в пузырьках, наоборот, понижено.
На основании ур-ния Кельвина рассчитывают заполнение капилляров или пористых тел при капиллярной конденсации. Т. к. значения р различны для частиц разных размеров или для участков пов-сти, имеющей впадины и выступы, ур-ние (3) определяет и направление переноса в-ва в процессе перехода системы к состоянию равновесия. Это приводит, в частности, к тому, что относительно крупные капли или частицы растут за счет испарения (растворения) более мелких, а неровности пов-сти некристаллич. тела сглаживаются за счет растворения выступов и залечивания впадин. Заметные различия давления пара и р-римости имеют место лишь при достаточно малых r0 (для воды, напр., при r0 [ 0,1 мкм). Поэтому ур-ние Кельвина часто используется для характеристики состояния коллоидных систем и пористых тел и процессов в них.
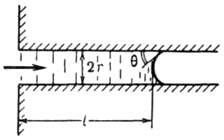
Рис. 2. Перемещение жидкости на длину l в капилляре радиуса r; q - краевой угол.
Капиллярная пропитка. Понижение давления под вогнутыми менисками - одна из причин капиллярного перемещения жидкости в сторону менисков с меньшим радиусом кривизны. Частным случаем этого является пропитка пористых тел - самопроизвольное всасывание жидкостей в лиофильные поры и капилляры (рис. 2). Скорость v перемещения мениска в горизонтально расположенном капилляре (или в очень тонком вертикальном капилляре, когда влияние силы тяжести мало) определяется ур-нием Пуазёйля:
где l - длина участка впитавшейся жидкости, h - ее вязкость, Dp - перепад давления на участке l, равный капиллярному
давлению мениска: Dp = — 2s12cos q/r. Если краевой угол q не зависит от скорости v, можно рассчитать кол-во впитавшейся жидкости за время t из соотношения:
l(t) = (rts12cos q/2h)l/2. (5)
Если q есть ф-ция v, то l и v связаны более сложными зависимостями.
Ур-ния (4) и (5) используют для расчетов скорости пропитки при обработке древесины антисептиками, крашении тканей, нанесении катализаторов на пористые носители, выщелачивании и диффузионном извлечении ценных компонентов горных пород и др. Для ускорения пропитки часто используют ПАВ, улучшающие смачивание за счет уменьшения краевого угла q. Один из вариантов капиллярной пропитки - вытеснение из пористой среды одной жидкости другой, не смешивающейся с первой и лучше смачивающей пов-сть пор. На этом основаны, напр., методы извлечения остаточной нефти из пластов водными р-рами ПАВ, методы ртутной порометрии. Капиллярное впитывание в поры р-ров и вытеснение из пор несмешивающихся жидкостей, сопровождающиеся адсорбцией и диффузией компонентов, рассматриваются физико-химической гидродинамикой.
Помимо описанных равновесных состояний жидкости и ее движения в порах и капиллярах, к капиллярным явлениям относят также равновесные состояния очень малых объемов жидкости, в частности тонких слоев и пленок. Эти капиллярные явления часто наз. капиллярными явлениями II рода. Для них характерны, напр., зависимость поверхностного натяжения жидкости от радиуса капель и линейное натяжение.
Капиллярные явления впервые исследованы Леонардо да Винчи (1561), Б. Паскалем (17 в.) и Дж. Жюреном (18 в.) в опытах с капиллярными трубками. Теория капиллярных явлений развита в работах П. Лапласа (1806), Т. Юнга (1804), А. Ю. Давыдова (1851), Дж. У. Гиббса (1876), И. С. Громеки (1879, 1886). Начало развития теории капиллярных явлений II рода положено трудами Б. В. Дерягина и Л. М. Щербакова.
===
Исп. литература для статьи «КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ»: Адамсон А., Физическая химия поверхностей, пер. с англ., М., 1979; Хейфец Л. И., Неймарк А. В., Многофазные процессы в пористых средах, М., 1982; Аксельруд Г. А., Альтшулер М. А., Введение в капиллярно-химическую технологию, М., 1983. Н. В. Чураев.
Страница «КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ» подготовлена по материалам химической энциклопедии.