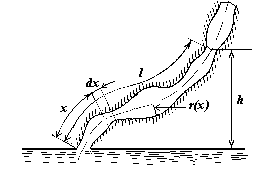
2.3.3. Смачивание как капиллярное явление.
Капиллярное впитывание

Осуществление значительного числа технологических процессов, в том числе и в текстильной промышленности, связано с пропиткой капиллярно-пористых тел. Текстильные материалы представляют собой классический пример капиллярных тел. Расчет скорости впитывания жидкости капиллярным телом, пронизанным капиллярами (среднего радиуса r и средней длиной l ),основан на использовании уравнения Пуазейля, описывающего скорость установившегося течения жидкости через капилляр, и уравнения Лапласа для избыточного давления в капилляре радиуса r.

Для объемной скорости течения V (м³/с) при установившемся режиме течения уравнение Пуазейля имеет вид

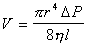, (1.2.62)

где r – радиус капилляра длиной l; h – вязкость жидкости, текущей через капилляр, DP – давление, под которым течет жидкость.

Движение жидкости по капиллярам осуществляется в результате действия капиллярного давления P_к, которое определяется углом смачивания Q жидкостью стенки капилляра, поверхностным натяжением жидкости s и радиусом капилляра r. Связь между всеми этими величинами описывается уравнением Лапласа:

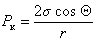, (1.2.63)

где s – поверхностное натяжение жидкости, Q – динамический угол смачивания, r – радиус кривизны, считающийся равным радиусу капилляра.

Если капилляры располагаются горизонтально, то можно не учитывать противодействие течению гидростатического давления жидкости. Если же они не горизонтальны, а располагаются к горизонтали под некоторым углом a , как это показано на рис. 1.26, то следует учитывать гидростатическое давление

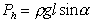, (1.2.64)

где r – плотность жидкости, g – ускорение силы тяготения.

Учитывая влияние гидростатического давления, можно записать для объемной скорости течения жидкости через капилляры ткани, в которой размеры капилляров неравномерны и поэтому следует ввести по длине некоторое значение эффективного радиуса r_е , учитывающего эту неравномерность размера,

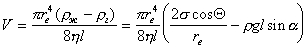. (1.2.65)

В уравнение (1.2.65) входят две неизвестные величины, не подлежащие прямому измерению, а именно эффективный радиус капилляров и динамический угол смачивания. Поэтому одну из этих величин исключают, поступая следующим образом. Очевидно, что в процессе смачивания ткани жидкость поднимается на высоту Н = l sin a и гидростатическое давление растет по мере увеличения высоты поднятия, в то время как капиллярное давление остается неизменным. Поэтому в некоторый момент времени t_к, достигнув некоторого значения длины l_max, впитывание прекратится вследствие равенства Р_к = Р_h.

Поэтому

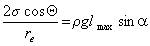, (1.2.66)

где l_max – предельная длина впитывания жидкости в капилляр.

Поэтому с учетом уравнения (1.2.66) запишем уравнение (1.2.65) в виде

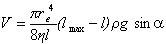. (1.2.67)

Заменим объемную скорость течения на линейную:

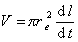. (1.2.68)

Из уравнений (1.2.67) и (1.2.68) следует

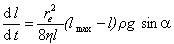. (1.2.69)

После разделения переменных получаем

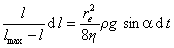. (1.2.70)

После интегрирования (1.2.70) в пределах от t =0 до t и от l=0 до l получаем

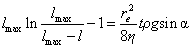. (1.2.71)

При вертикальном положении капилляров sin a =1, тогда

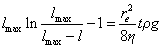. (1.2.72)

Уравнение (1.2.72) называют уравнением Уошборна, его можно использовать для определения эффективного радиуса капилляров r_e , так как все остальные величины поддаются непосредственному экспериментальному определению.

Если капилляры горизонтальные, то гидростатическое давление не оказывает влияния на скорость впитывания жидкости, поэтому из уравнений (1.2.65) и (1.2.68) при Р_h =0 следует

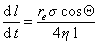. (1.2.73)

После интегрирования уравнения (1.2.73) в пределах от t =0 до t и от l =0 до l получаем

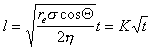. (1.2.74)

Уравнение (1.2.74) может быть использовано и на начальных стадиях впитывания жидкости в капилляр при условии

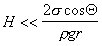. (1.2.75)

Уравнения (1.2.72) и (1.2.74) были впервые получены Уошборном, предложившим учитывать сопротивление воздуха в капиллярах.

Этот подход реализуется также при рассмотрении капиллярного вытеснения одной жидкости другой, например, при вытеснении масляных загрязнений из капилляров ткани растворами ПАВ. В этом случае уравнение капиллярной пропитки принимает вид

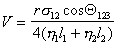, (1.2.76)

где l₁, l₂ – длина участков капилляра, занятых соответственно жидкостями 1 и 2, имеющими вязкость h₁ и h₂ ; s₁₂– межфазное натяжение на границе этих жидкостей; Q₁₂₃ – угол смачивания на границе двух жидкостей с твердым телом.