2.3.4. Гистерезис смачивания

Ранее мы рассмотрели зависимости равновесного смачивания жидкостью поверхности идеального недеформируемого твердого тела. Для таких систем нет различия в механизме достижения равновесия - будет ли оно достигнуто при натекании жидкости на поверхность или при ее отекании. Для реальных тел с шероховатой поверхностью, на которой возможны загрязнения или адсорбционные пленки, значение равновесного угла смачивания зависит от предыстории достижения равновесия.

В большинстве случаев смачивания жидкостью поверхности твердого тела краевой угол натекания и угол отекания жидкости не равны, причем угол натекания всегда больше. Разница между этими углами составляет десятки, а иногда и сотни градусов. Например, угол натекания капли ртути на стали на 154^o больше угла отекания. Очевидно, что для практических расчетов необходимо знать, каким образом был измерен угол смачивания. Можно назвать, по крайней мере, три причины различия в углах натекания и отекания. Первая из них – неоднородность поверхности, например ткани, в результате загрязнения каким-либо гидрофобным веществом, например маслом. В этом случае при смачивании поверхности водой масляное загрязнение будет растекаться по поверхности воды и снижать ее поверхностное натяжение, а поверхность твердого тела после удаления масляной пленки и отступания капли воды будет иметь более высокое поверхностное натяжение.

Анализ уравнения Юнга (1.2.45) 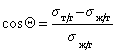показывает, что угол смачивания при отекании в этом случае будет меньше угла натекания.

Тщательная предварительная очистка поверхности твердого тела в значительной степени исключает гистерезис смачивания, особенно если твердое тело нерастворимо в жидкости и имеет гладкую поверхность.

Вторая причина гистерезиса – шероховатость твердого тела, влияние которой на величину краевого угла смачивания мы обсудили выше. Поскольку углы натекания чаще бывают тупыми (Q_н > 90^o), а углы отекания острыми (Q_о< 90^o), то шероховатость увеличивает угол натекания и снижает угол отекания. Отметим, что шероховатость должна быть соизмерима с размером капли, иначе ее влияние будет незначительным. Практически все поверхности шероховаты на микроскопическом уровне, но такой вид шероховатости не оказывает влияния на смачивание. При макроскопической шероховатости возможно запирание пузырьков воздуха и поверхность твердого тела ведет себя как составная, что резко повышает величину углов натекания.

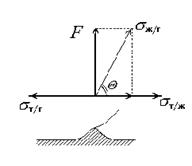
Третья причина состоит в подвижности (или неподвижности) поверхности твердого тела в макроскопическом масштабе. Если поверхность способна деформироваться под действием молекулярных сил притяжения и по периметру смачивания формируется валик, этот валик способен оказывать такое же влияние на угол смачивания, как и шероховатость, рис. 1.27. Образование валика происходит под действием нескомпенсированной нормальной составляющей силы поверхности .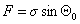

Такая деформация видна невооруженным глазом на свежих набухших полимерных пленках, например на геле желатина. При перемещении фронта смачивания происходит смещение волны поверхностной деформации. Такой фактор вполне может проявляться и при смачивании полимерных волокон, особенно эластичных.

Скорость движения жидкости также оказывает влияние на величину краевого угла смачивания. При увеличении скорости течения угол смачивания растет и становится тем больше равновесного значения, чем выше скорость течения. В этом случае говорят о динамическом угле смачивания.

Для расчета величины динамического угла смачивания при течении в режиме с малым значением критерия Нуссельта 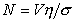используют уравнение

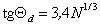, (1.2.77)

где V – скорость течения; h , s – вязкость и поверхностное натяжение текущей жидкости.

Для определения значений динамического угла смачивания измеряют скорость капиллярного впитывания жидкости с использованием приведенного выше уравнения (1.2.72) Уошборна при вертикальном расположении капилляров. При выражении скорости течения как

,

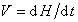где Н – высота жидкости в капилляре радиуса r, t– время, уравнение Уошборна принимает вид

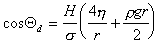. (1.2.78)

Расчет Q_d по этому уравнению позволяет получить значения, достаточно хорошо совпадающие с измеренными экспериментально.