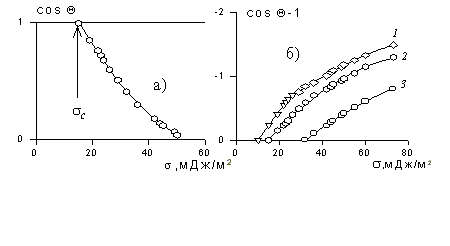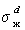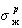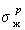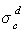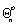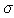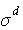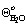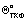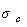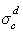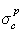2.3.2. Смачивание и растекание на границе твердое тело – жидкость – газ

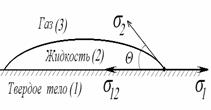
В большинстве случаев жидкость на поверхности твердого тела остается в виде капли, большей или меньшей толщины, контактирующей с твердым телом под определенным углом, который называется краевым углом смачивания и обозначается буквой Q (рис. 1.24). Растекание капли по поверхности прекратится при достижении равновесия, которое без учета сил тяжести может быть описано уравнением Юнга:

(1.2.44)

или

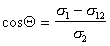, (1.2.45)

где индексы 1, 2, 3 – обозначают, соответственно, твердую, жидкую и газовую фазы.

Работа адгезии выражается уравнением Дюпре:

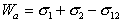(1.2.46)

или

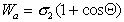. (1.2.47)

Работа адгезии при 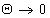,т.е. при полном смачивании, 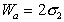, что эквивалентно работе когезии жидкости. Если Q = 180^o, соs Q = -1 и в соответствии с уравнением (1.2.47) W_a = 0, т.е. жидкость не смачивает твердую поверхность. При Q» 90^o жидкость проявляет слабое смачивание.

Следует помнить, что определение работы адгезии в реальных системах предполагает равновесие фаз, насыщенных относительно друг друга.

Кроме того, твердая поверхность, по которой происходит растекание жидкости, не свободна. Она обычно покрыта пленкой вещества, адсорбированного из газо-паровой фазы. Эта пленка имеет поверхностное давление p, поэтому

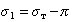, (1.2.48)

где s _т - поверхностное натяжение «чистого» твердого тела на границе с воздухом.

Смачивание неоднородных, пористых или шероховатых поверхностей сопровождается запиранием пузырьков воздуха в неровностях. В результате этого краевые углы смачивания сухой и предварительно увлажненной поверхностей различаются. Такое явление носит название «гистерезис смачивания». Гистерезис смачивания проявляется также при загрязнении поверхности, в результате чего она становится неоднородной при закреплении на ней твердых частиц или жировых пленок. В этом случае поверхность ведет себя как составная.

Шероховатость поверхности учитывается введением коэффициента шероховатости r, представляющего отношение площади поверхности реального тела к площади идеально гладкой поверхности, тогда

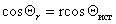. (1.2.49)

Можно отметить, что если краевой угол смачивания гладкой поверхности, например полимерной пленки, меньше 90^o, то шероховатость (ткань из волокон этого полимера) уменьшает его, если же он больше 90^o, то шероховатость его увеличивает. Для составной поверхности, которая специфична для большинства текстильных материалов, наличие участков различной природы может быть учтено введением коэффициентов x, характеризующих долю поверхности с различными свойствами. Например, если текстильный материал изготовлен из волокон двух видов 1 и 2, то

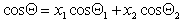. (1.2.50)

Если переплетение нитей таково, что получается сетчатый или дырчатый материал, то уравнение (2.50) принимает вид

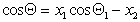, (1.2.50')

где х₂ – доля открытой поверхности.

Как мы обсуждали выше, поверхностное натяжение можно разделить на компоненты дисперсионных и полярных сил, а при нахождении межфазового натяжения для многих жидких границ можно ограничиться лишь дисперсионной составляющей. Такое ограничение позволяет провести обсуждение явления смачивания (по крайней мере, низкоэнергетических поверхностей, к каковым можно отнести подавляющее большинство волокнообразующих полимеров), в рамках теории дисперсионных сил.

Как показал Н. В. Чураев смачивание неполярной жидкостью твердой поверхности возможно, если будет соблюдаться условие смачивания, которое выражается уравнением

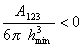, (1.2.51)

где А₁₂₃ – составная постоянная Гамакера при взаимодействии жидкости (фаза 2) с твердым телом (фаза 1) на границе с воздухом (фаза 3); h_min - наименьшая толщина пленки, которая фактически соответствует Ван-дер-Ваальсову расстоянию, т.е. h_min = (0,22¸0,24) нм. Например, для воды на поверхности тефлона А₁₂₃ = -7·10^-21 Дж.

Учет только дисперсионных сил приводит к уравнению

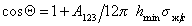, (1.2.52)

гдеs _ж/г – поверхностное натяжение жидкости.

При расчетах углов смачивания твердых поверхностей следует учитывать поверхностное давление пленки, образованной при адсорбции из газо-паровой фазы. Тогда с учетом уравнения (1.2.48), уравнение Юнга (1.2.45) следует записать в виде

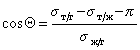. (1.2.53)

Способ расчета поверхностного давления предложили Бэнгхэм и Разорук:

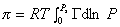, (1.2.54)

где P – равновесное давление, Г– равновесная адсорбция газа (пара), P_s – давление насыщения.

При больших углах смачивания и слабом взаимодействии жидкости с твердым телом поверхностное давление обычно не учитывают.

Для неполярных жидкостей на низкоэнергетической поверхности твердого тела для работы адгезии было получено выражение

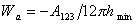. (1.2.55)

Поэтому уравнение Дюпре (1.2.46) можно записать

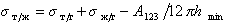. (1.2.55')

Для дисперсионной составляющей жидкости

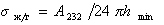, (1.2.56)

где А₂₃₂ – постоянная Гамакера взаимодействия жидкости через прослойку газа (пара).

Сочетая уравнения (1.2.47), (1.2.55) и (1.2.56), получаем

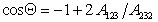. (1.2.57)

Очевидно, что Q = 0, т.е. при полном смачивании, cosQ = 1, если

А₁₂₃= А₂₃₂.

Уравнение (1.2.57) позволяет прогнозировать вероятность смачивания (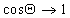) или наоборот - несмачивания (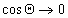) жидкостью поверхности твердого тела по известным постоянным межмолекулярных сил взаимодействия.

Чаще, однако, прибегают к определению постоянной Гамакера по известному значению межфазового натяжения на границе «твердое тело - газ». Эту характеристику поверхности твердого тела находят при распространении подхода Джирифалько и Гуда, рассмотренного нами выше для границы двух жидкостей, на поверхность раздела «жидкость - твердое тело», уравнения (1.2.23), (1.2.35).

Так приложение уравнения (1.2.34) к уравнению Юнга для случая смачивания неполярной жидкостью поверхности полимерного материала позволяет получить уравнение, известное как уравнение Фоукса, при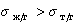

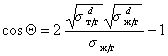. (1.2.58)

Если жидкости неполярны и 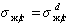, то уравнение (1.2.58) переходит в уравнение

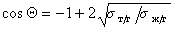. (1.2.59)

Уравнение (1.2.59) Зисман предложил использовать для определения поверхностного натяжения твердых тел. Очевидно, что при 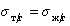cosQ =1, а угол смачивания будет равен нулю (Q = 0), т.е. наступает полное смачивание.

Естественно, что метод Зисмана ограничен некоторыми условиями, в частности, из уравнения (1.2.57) следует, что полное смачивание возможно при дисперсионной неразличимости твердого тела и жидкости, т.е. при А₂₃₂= А₁₂₃.

В действительности такого условия никогда невозможно достигнуть хотя бы потому, что если жидкость и твердое тело будут иметь одинаковый химический состав, их постоянные Гамакера будут различаться из-за различий в плотности.

Другое ограничение, связанное с применением метода Зисмана, основано на том, что использовать для измерения краевых углов смачивания следует лишь неполярные жидкости. Наиболее целесообразно применять гомологические ряды жидкостей. При величине поверхностного натяжения жидкостей более 35 мДж/м² метод Зисмана уже дает высокую погрешность, так как необходимо учитывать вклад полярных сил, которые в отличие от дисперсионной составляющей могут иметь и отрицательное значение. С другой стороны, приложение для смачивания твердых тел полярными жидкостями уравнения Ву (1.2.36) позволяет рассчитать полярную составляющую поверхностного натяжения жидкости, если для одной из неполярных жидкостей измерить краевой угол смачивания. Для расчета используют уравнение

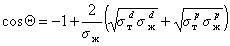. (1.2.60)

Этот метод позволил разделить величину поверхностного натяжения жидкостей на полярную и дисперсионную компоненты и определить поверхностное натяжение многих волокнообразующих полимеров.

Пример зависимости косинуса угла смачивания поверхности пленок различными жидкостями приведен на рис.1.25. Для описания этих зависимостей Зисман предложил использовать эмпирическое уравнение

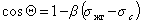, (1.2.61)

где bэмпирическая постоянная, s_с – «критическое» поверхностное натяжение твердого тела, при котором происходит полное смачивание твердого тела жидкостью. Очевидно, что cos Q =1 при условии s_жг = s_с .

Как мы обсуждали выше, этот критерий в известной мере является условным, хотя и отражает энергетическое состояние поверхности твердого тела.

Реальное значение поверхностного натяжения твердого тела экспериментально определить невозможно, также как и рассчитать его теоретически. В этой связи метод Зисмана нашел широкое применение в практике исследования полимерных материалов, а также полимерных покрытий тканей, используемых в качестве отделочных материалов

Таблица 1.2

Значения поверхностного натяжения жидких и твердых веществ,

при Т=293 К по данным М.Saito

Из приведенных на рис. 1.25 зависимостей видно, что линейность соблюдается только в области поверхностных натяжений жидкостей, не слишком отличающихся от величины критического поверхностного натяжения твердой поверхности, которую находят путем экстраполирования линейного участка зависимости к величине cos Q = 1 (рис. 1.25, а) или cos Q- 1 = 0 (рис. 1.25, б). Целесообразно проводить определение критического поверхностного натяжения твердых тел при использовании жидкостей одинакового строения, например только алканов или только спиртов, и т.д.

Найденные методом Ву значения инкрементов поверхностного натяжения некоторых веществ приведены в табл. 1.2 и 1.3.

Таблица 1.3

Угол смачивания и поверхностное натяжение при Т= 293 К

Q_n, 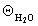,Q_ткф – углы смачивания парафина жидкостью, смачивания твердого вещества водой и трикрезилфосфатом; s_c – критическое поверхностное натяжение; индексы d и p соответствуют дисперсионной и полярной составляющим.