Характеристика взаимодействий в адсорбционном слое

Для характеристики энергии взаимодействия ионов или молекул в адсорбционном слое обычно используется величина изостерической (т.е. при постоянстве адсорбции) теплоты адсорбции, которая рассчитывается по уравнению

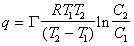, (1.5.32)

где С₁,С₂ – равновесные концентрации, соответствующие постоянной адсорбции Г при температурах Т₁ и Т₂.

Типичная зависимость изостерической теплоты адсорбции от степени заполнения адсорбционного слоя приведена на рис. 1.53. Величины qхарактерны для ван-дер-ваальсовой адсорбции и составляют 10-20 кДж/моль. До степени заполнения 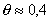в адсорбционном слое преобладают взаимодействия полярных групп, выше 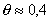- латеральные взаимодействия адсорбат-адсорбент. Катионоактивное ПАВ адсорбируется с вытеснением неорганических противоионов, причем обмен происходит необратимо и преимущественно в плотной части (слой Штерна) двойного слоя вследствие электростатического взаимодействия положительно заряженных ионов ПАВ с фиксированными отрицательно заряженными группами поверхности. При насыщении мономолекулярного слоя катионных ПАВ, т.е. при взаимодействии всех доступных для адсорбции диссоциированных поверхностных групп с органическим катионом, поверхностный потенциал, характеризуемый экспериментальной величиной z-потенциала, будет равен нулю (изоэлектрическое состояние). Причем совсем необязательно, что углеводородные радикалы будут располагаться нормально к поверхности. Они могут взаимодействовать и с гидрофобными участками поверхности волокна. В состоянии ИЭТ. проявляется только специфическое взаимодействие адсорбат-адсорбент. Выше ИЭТ. 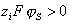, так как штерновский потенциал меняет знак, и электрическое взаимодействие будет препятствовать адсорбции.

По величине адсорбции катионоактивных ПАВ G_ИЭТ в изоэлектрическом состоянии поверхности можно определить поверхностную плотность заряда адсорбента:

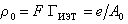, (1.5.33)

где е – элементарный заряд; А₀ – площадь молекулы ПАВ в насыщенном монослое. Можно рассчитать поверхностную плотность заряда, зная обменную емкость Е и удельную поверхность адсорбента:

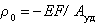. (1.5.34)

Зависимость плотности заряда в штерновском слое от равновесной концентрации раствора ПАВ можно рассчитать, используя подход Штерна-Грэма по уравнению

, (1.5.35)

в предположении постоянства плотности поверхностного заряда 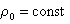и линейной зависимости адсорбции от равновесной концентрации в области разбавленных растворов (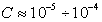моль/л). Здесь В – адсорбционная постоянная, учитывающая латеральные взаимодействия.

Постоянную В определяют из очевидного условия, что в ИЭТ., т.е. при С=С_ИЭТ, электрокинетический z и Штерновский 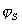потенциалы, а также диффузный заряд r_dравны нулю.

Из условия электронейтральности

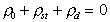(1.5.36)

следует, что 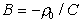_ИЭТ , поэтому для любой концентрации

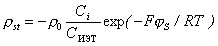. (15.37)

Величину 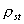можно рассчитать также из величины равновесной адсорбции:

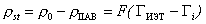. (1.5.38)

При малой концентрации растворов ПАВ диффузную 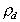и поверхностную 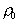плотность зарядов для сферических частиц можно рассчитать по уравнениям

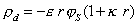, (1.5.39)

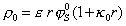, (1.5.40)

где 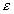– диэлектрическая проницаемость среды; r – радиус частиц; 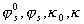– штерновский потенциал и параметр Дебая до и после адсорбции ПАВ.

Вводя в выражения для 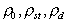условие электронейтральности, можно получить для сферических частиц уравнение для расчета штерновского потенциала в зависимости от концентрации ПАВ:

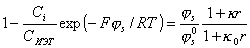(1.5.41)

При низких концентрациях фоновых электролитов в растворах можно принять . Значения С_ИЭТ находят по зависимост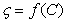и при 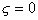. Для расчета r₀ необходимо измерять адсорбцию ПАВ в изоэлектрической точке. Уравнения (1.5.38), (1.5.39), (1.5.41) дают возможность оценить влияние заряда поверхности на адсорбцию заряженных молекул ПАВ. Они же могут быть использованы для расчета толщины неподвижной (штерновской) части двойного слоя, которую следует знать при проведении некоторых термодинамических расчетов и при оценке стабилизирующего (очищающего) действия ПАВ. Например, одним из возможных способов расчета сродства адсорбированных молекул (красителя или ПАВ) к адсорбенту может быть определение коэффициента распределения адсорбата между раствором и адсорбционным слоем (слоем Штерна):

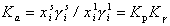(1.5.42)

где 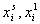– молярные доли i-того компонента системы, например, ПАВ, в адсорбционном слое и в равновесном растворе; 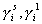– соответствующие коэффициенты активности; 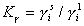– стремится к единице в области разбавленных растворов и адсорбционного слоя, далекого от насыщения, т.е. при 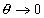; K_р – коэффициент распределения, для расчета которого необходимо знать концентрации адсорбата как в растворе, так и в адсорбционном слое. Для этого требуется определять объем адсорбированного раствора. Этот объем (отнесенный к единице массы адсорбента) рассчитывается как произведение поверхности на толщину неподвижной части адсорбционного слоя, т.е.

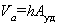. (1.5.43)

При физической адсорбции, т.е. в изоэлектрическом состоянии поверхности, при концентрациях, соответствующих бесконечно разбавленным раствору и адсорбционному слою,

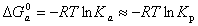. (1.5.44)

Для определения толщины адсорбционного слоя можно воспользоваться уравнением теории строения двойного ионного слоя Гуи- Чепмена, предполагая, что адсорбционный слой неподвижен и разрыв двойного слоя проходит по его границе:

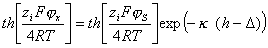, (1.5.45)

где

,

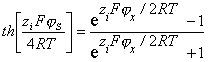– толщина слоя Штерна (=0,3¸0,5нм); h – толщина неподвижного слоя жидкости; 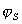– потенциал слоя Штерна, рассчитанный по адсорбции.

При малых величинах 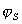и z (менее 50 мВ) уравнение (1.5.45) переходит в

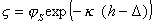, (1.5.46)

откуда

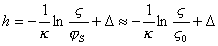. (1.5.47)

Расчеты, основанные на измерении адсорбции катионоактивных ПАВ и электрокинетического потенциала, показывают, что толщина граничного слоя h составляет 10-20 нм и уменьшается в результате вытеснения воды по мере заполнения поверхности молекулами ПАВ, достигая минимального значения при насыщении адсорбционного слоя.

Учет взаимодействий между адсорбированными молекулами (ионами) с атомами поверхности и между собой проведен в уравнении Хилла, которое отличается от уравнения Фольмера (1.5.15) дополнительным членом 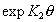и имеет вид

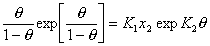, (1.5.48)

или в линейной форме

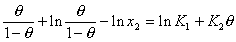. (1.5.49)

Постоянная K₁ отражает постоянную адсорбционного равновесия K_а, так как

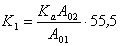, (1.5.50)

где А₀₁, А₀₂ – площади ван-дер-ваальсовых проекций молекул воды и ПАВ в адсорбционном слое; K₂– учитывает межмолекулярное (латеральное) взаимодействие в адсорбционном слое, которое проявляется в отклонении коэффициента активности адсорбированных молекул ПАВ от единицы.

Построение изотерм адсорбции в линейной форме уравнения Хилла (1.5.49) позволяет определить постоянных K₁ и K₂, рассчитать энергию Гиббса адсорбции и охарактеризовать межмолекулярные взаимодействия в адсорбционном слое. Следует отметить, что уравнение Хилла (1.5.48) достаточно строго описывает изотерму адсорбции до степени заполнения адсорбционного слоя 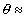0,75.

Экстраполяцию к бесконечному разбавлению адсорбционного слоя для нахождения постоянной адсорбционного равновесия можно проводить и в координатах ln(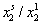) - 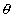, как это было описано выше.