4.1.2 Основы теории строения двойного ионного слоя
Современные представления о строении двойного ионного слоя сложились в результате эволюции взглядов на его структуру. Первоначально предполагалось, что ДИС имеет вид плоского конденсатора. Теоретическое рассмотрение такого слоя впервые описано в работах Гельмгольца (1879 г.). Последующее развитие этих представлений было проведено Перреном (1904 г.).
В соответствии с такой моделью поверхностный потенциал может быть рассчитан, как
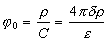 , (1.4.3)
, (1.4.3)
где r– поверхностная плотность заряда,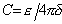 -емкость единицы площади раздела фаз, d– расстояние между обкладками конденсатора, e- диэлектрическая постоянная.
-емкость единицы площади раздела фаз, d– расстояние между обкладками конденсатора, e- диэлектрическая постоянная.
При рассмотрении двойного ионного слоя как плоского конденсатора предполагалось, что внутренняя обкладка его образована зарядами, фиксированными на поверхности твердого тел, а внешняя - зарядами, локализованными в жидкости. Считалось, что количество потенциалопределяющих и противоионов в двойном ионном слое эквивалентно. Ионы рассматривались как точечные заряды. Слой жидкости, непосредственно прилегающий к поверхности, остается неподвижным в электрическом поле. Толщина двойного слоя считалась незначительной и соответствовала примерно двум молекулярным слоям.
Таким образом, в теории Гельмгольца-Перрена не учитывалось тепловое движение ионов, и предпосылка об эквивалентности потенциалопределяющих и противоионов в двойном ионном слое оказалась несостоятельной. На этот факт обратили внимание, независимо друг от друга Гуи (1910 г.) и Чепмен (1913 г.), которые отметили, что избыток ионов одинакового знака не может быть сосредоточен на межфазной границе, но обязательно вследствие теплового движения они (ионы) будут распределяться в виде диффузионной оболочки. Протяженность этой оболочки определяется конкуренцией электростатического взаимодействия противоионов с потенциалопределяющими с одной стороны и тепловым движением противоионов - с другой. Такая предпосылка предполагает плавное изменение потенциала внутри ДИС от величины поверхностного потенциала j0до нуля внутри раствора. При этом в пределах ДИС концентрация ионов, одноименных с потенциалопределяющими, изменяется от нуля до величины, соответствующей концентрации в растворе. Одновременно с этим концентрация противоионов, имеющая максимальную величину вблизи поверхности фаз, снижается до величины, равной концентрации ионов противоположного заряда для симметричных электролитов (т.е. электролитов с одинаковым по величине зарядом ионов) или эквивалентной ей (для прочих электролитов).
Распределение противоионов диффузионной части двойного ионного слоя зависит от их природы, концентрации электролитов в растворе и от температуры. Предполагается, что это распределение подчиняется закону распределения Больцмана
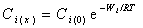 , (1.4.4)
, (1.4.4)
где 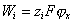 – работа перемещения 1 кг-экв. ионов с бесконечно большого расстояния в точку x двойного ионного слоя; jx– потенциал в этой точке; Сi(x), Сi(0)- концентрация ионов i – того сорта на расстоянии х от поверхности и в растворе (кмоль/м3 ); zi– заряд иона (с учётом знака).
– работа перемещения 1 кг-экв. ионов с бесконечно большого расстояния в точку x двойного ионного слоя; jx– потенциал в этой точке; Сi(x), Сi(0)- концентрация ионов i – того сорта на расстоянии х от поверхности и в растворе (кмоль/м3 ); zi– заряд иона (с учётом знака).
Предполагается, что объёмная плотность заряда в точке х диффузного слоя rxописывается уравнением
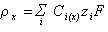 . (1.4.5)
. (1.4.5)
В объеме раствора rx = 0 (условие электронейтральности).
Для аналитического совместного решения уравнений (1.4.4) и (1.4.5) следует ввести предпосылки, сделанные Гуи и Чепменом :
1) двойной ионный слой является плоским, т.е. предполагается, что радиус кривизны поверхности твердого тела значительно больше толщины ионного слоя, т.е. r > 1/k, где k - параметр Дебая, равный обратной величине протяженности двойного ионного слоя;
2) диэлектрическая проницаемость растворителя в пределах ДИС считается постоянной, независимо от расстояния до поверхности;
3) предполагается, что для перевода ионов из раствора в точку хследует совершить работу лишь против сил электрического взаимодействия;
4) считается, что собственный объем ионов исчезающе мал, т.е. рассматриваются точечные заряды;
5) считается, что распределение ионов в пределах двойного ионного слоя подчиняется закону распределения Больцмана.
Удобным для расчетов является случай симметричного бинарного электролита, для которого 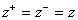 . При этих условиях были получены уравнения для поверхностей с потенциалом не более 50·10-3В :
. При этих условиях были получены уравнения для поверхностей с потенциалом не более 50·10-3В :
– для плотности заряда на поверхности
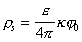 , (1.4.6)
, (1.4.6)
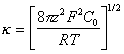 , (1.4.7)
, (1.4.7)
где j0 – потенциал поверхности, k – параметра Дебая, С0 – концентрация ионов в растворе;
– для зависимости потенциала от расстояния до поверхности
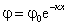 . (1.4.8)
. (1.4.8)
Величина 1/k эквивалентна понятию «радиус ионной атмосферы», введенному в теорию растворов сильных электролитов Дебаем позднее создания теории Гуи-Чепмена.
Для любых значений j0 и, следовательно, j Овербек получил выражение
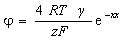 (1.4.9)
(1.4.9)
где
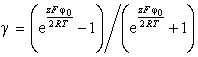 . (1.4.10)
. (1.4.10)
Из уравнения (1.4.6) можно видеть, что поверхностный заряд пропорционален потенциалу поверхности.
При течении жидкости, как известно, скорость течения ее вблизи поверхности равна нулю и возрастает по мере удаления от нее. Плоскость, которая отделяет слой неподвижной жидкости вблизи стенки от жидкости, текущей по капилляру, и разделяет двойной ионный слой на две части, называется плоскостью скольжения. Потенциал на этой плоскости называют электрокинетическим, и обозначают буквой z (дзета). Обычно считается, что этот потенциал равен электрическому потенциалу на расстоянии D от поверхности твердой фазы, т.е. 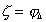 . Хотя концентрация ионов в растворе не влияет на потенциал поверхности, электрокинетический потенциал снижается пропорционально С1/2.
. Хотя концентрация ионов в растворе не влияет на потенциал поверхности, электрокинетический потенциал снижается пропорционально С1/2.
В этом основное отличие электрокинетического потенциала от термодинамического. Причем z-потенциал может изменяться в пределах от z = j0 при концентрации электролита в растворе 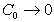 до
до 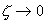 при высоких значениях С0. В соответствии с теорией во всех случаях j0 и z-потенциалы должны иметь один знак. Эти рассуждения не справедливы для ионов, отнесенных ранее к группе 1, повышение концентрации которых приводит к росту потенциала поверхности. Кроме того, теория Гуи-Чепмена не может объяснить наблюдающиеся на практике случаи, когда электрокинетический и термодинамический потенциалы имеют различный знак.
при высоких значениях С0. В соответствии с теорией во всех случаях j0 и z-потенциалы должны иметь один знак. Эти рассуждения не справедливы для ионов, отнесенных ранее к группе 1, повышение концентрации которых приводит к росту потенциала поверхности. Кроме того, теория Гуи-Чепмена не может объяснить наблюдающиеся на практике случаи, когда электрокинетический и термодинамический потенциалы имеют различный знак.
Можно отметить, что теория Гуи-Чепмена хорошо объясняет качественное различие между j0 и z-потенциалами, влияние на электрокинетический потенциал индифферентных (непотенциал- определяющих) ионов, но она не в состоянии объяснить, например, изменение знака z-потенциала при повышении концентрации некоторых электролитов и дает завышенное на порядок значение емкости двойного ионного слоя.
Дальнейшее развитие теория строения двойного ионного слоя получила в работах Штерна (1924 г.). Штерн отметил, что ионы, образующие диффузную часть ДИС, распределяются в ней не только под действием сил электростатического взаимодействия и теплового движения, но и под влиянием адсорбционного взаимодействия с твердой поверхностью. Для учета этого взаимодействия Штерн использовал введенное им понятие «специфического» адсорбционного потенциала. Как показывают исследования, эти силы могут быть значительными, что способно, например, приводить к сверхэквивалентной по отношению к потенциалопределяющим ионам адсорбции поливалентных противоионов. Образующийся адсорбционный слой, как правило, мономолекулярный. Если адсорбируются ионы одного типа, то на межфазной поверхности накапливается некоторое количество электричества и потенциал вблизи поверхности jD будет отличаться от j0подчас не только по величине, но и по знаку.
Главным в модели Штерна является разделение двойного слоя на две части, внутреннюю и внешнюю.Во внешней части адсорбционные силы и собственный размер гидратированных ионов не учитываются, так как предполагается, что протяженность действия сил, обусловливающих специфическую адсорбцию, в отличие от электростатических, столь мала, что учет их важен только на расстоянии, соответствующем размеру гидратированного иона. Распределение потенциала в диффузной части двойного слоя можно описать уравнением теории Гуи-Чепмена. Внутреннюю часть Штерн описал на основании теории мономолекулярной адсорбции Ленгмюра, расширив представление об адсорбции на активных участках ионов. Потенциал jD часто называют штерновским. Слой потенциалопределяющих ионов и слой специфически адсорбированных ионов образуют как бы плоский конденсатор. Заряд поверхности с плотностью rs компенсирован суммой зарядов второй обкладки плоского конденсатора (внутренний слой) rst и внешнего (диффузного) слоя rd. Полное падение потенциала в пределах двойного ионного слоя будет слагаться из падения потенциала диффузионной части и потенциала в плотной части j0-jD. Положение плоскости скольжения в рассматриваемой модели остается неясным. Часто полагают, что плоскость скольжения совпадает с границей, разделяющей слой Штерна от слоя Гуи. При этом считают, что 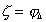 . Однако в более общем случае можно представить, что плоскость скольжения проходит в слое Гуи.
. Однако в более общем случае можно представить, что плоскость скольжения проходит в слое Гуи.
Термин «специфическая» адсорбция не имеет четкого определения, но чаще всего полагают, что к «специфической» адсорбции следует относить такую, в процессе которой количество адсорбированного заряженного вещества различно для ионов одинакового заряда в результате наложения на электростатическое взаимодействие межмолекулярных сил притяжения. В соответствии с этим «неспецифической» следует называть адсорбцию, одинаковую для ионов одинакового по величине и знаку заряда, т.е. ионов одного сорта. Именно такая адсорбция ионов в диффузионной части двойного ионного слоя описывается уравнением распределения статистики Пуассона-Больцмана. Адсорбция ионов в недиффузионной части двойного слоя должна рассматриваться как «специфическая», не подчиняющаяся закону распределения Больцмана. Такая адсорбция зависит от размера гидратированного иона и приводит к лиотропным рядам.
Согласно такой формулировке потенциалопределяющие ионы, расположенные непосредственно на поверхности раздела фаз, тоже следует рассматривать как «специфически» адсорбированные.
В соответствии с классификацией по типу адсорбции все заряженные молекулы (ионы) текстильно-вспомогательных веществ, молекулы активных красителей должны рассматриваться как адсорбирующиеся «специфически» и при их адсорбции рассматриваются две составляющие свободной энергии, а именно электростатическая и молекулярная. Последнюю, в свою очередь, можно разделить на полярную и неполярную компоненты.
Чтобы упростить изображение схемы и одновременно подчеркнуть сложность состава коллоидной частицы Дюкло (1908 г.) предложил использовать специальный термин «мицелла», введенный в науку в 1858 г. Нагели.
При образовании труднорастворимых соединений энергия гидратации меньше энергии кристаллической решетки, что способствует прочной фиксации адсорбируемых потенциалопределяющих ионов. Эти представления Фаянс использовал для объяснения образования коллоидных систем (на примере галоидов серебра). Например, в результате реакции AgNO3 с избытком КIобразуется кристаллик AgI, который по предложенной Н.П. Песковым (1934 г.) терминологии называют агрегатом. Действительно, эта часть мицеллы всегда состоит из агрегата атомов. Агрегат совместно с адсорбированными на нем потенциалопределяющими (nI-) ионами называют ядром мицеллы. В рассматриваемом случае схема мицеллы будет изображаться условной формулой, представленной на рис.1.36.

Рис. 1.36. Схема мицеллы
Вертикальные фигурные скобки разделяют слои, определяя плоскость скольжения; (n- x)K+ - противоионы, расположенные в плотной части, физически адсорбированные в слое Штерна; xK+ – противоионы, распределенные в диффузионной части двойного слоя.
На поверхности частицы будут всегда адсорбироваться те ионы, которые способны достраивать кристаллическую решетку, или изоморфные им. Так, кристаллик AgI будет способен адсорбировать не только ионы I-, но и Сl-, Br-.
Теория Штерна распространяется не только на твердые частицы с четко выраженной границей раздела, но и на системы, в которых граница раздела фаз размыта, например, на волокна, набухающие в водных растворах, или даже при отсутствии поверхности раздела, что характерно для растворов белков и полиэлектролитов. В любом случае в системе должно устанавливаться электрохимическое равновесие. При большом количестве ионогенных групп или активных центров на частицах уравнение закона действующих масс, используемое для описания степени диссоциации поверхностных ионогенных групп, и уравнение изотермы адсорбции Ленгмюра совпадают. Это позволяет использовать теорию Штерна для описания процессов в разнообразных системах. Адсорбция заряженных частиц (ионов) может считаться специфической, если она сопровождается следующими эффектами:
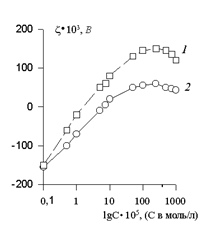
Рис.1.37. Зависимость электрокинетического потенциала золя красителя кристаллического фиолетового при добавлении электролитов: 1 - Аl(NO3)3, 2 - Th(NO3)4 |
1. Изменением знака электрокинетического потенциала zс увеличением концентрации иона в растворе при постоянном или возрастающем поверхностном потенциале. Схематично такой случай приведен на рис. 1.37. Такое изменение z-потенциала возможно при сверхэквивалентной (по отношению к потенциалопределяющим ионам) адсорбции противоионов в слое Штерна. Очевидно, что при отсутствии специфической адсорбции такой эффект невозможен, так как адсорбция в данном случае определяется лишь электрической компонентой (ZiFj). Изменение знака z-потенциала приводит к появлению «неправильных» рядов коагуляции, т.е. вместо ожидаемой коагуляции к повышению устойчивости гидрофобных коллоидных систем при добавлении в них электролитов, содержащих поливалентные ионы. Неправильные ряда коагуляции также свидетельствуют о специфической адсорбции.
2. Смещением точки нулевого заряда (ТНЗ) и изоэлектрической точки (ИЭТ) при прочих равных условиях. Направление сдвига указывает на знак заряда иона, который адсорбируется специфически, если D(ТНЗ)>0, а D(ИЭТ)< 0, то адсорбируется анион. При перемене знаков - специфическая адсорбция катиона.
Если на поверхности раздела фаз имеются потенциалопределяющие ионы Н+ и ОН-, то при отсутствии специфической адсорбции (ТНЗ) и (ИЭТ) совпадают, при добавлении какого-либо электролита K+А-, у которого специфически адсорбируется анион А‑, в то время как катион K+ взаимодействует лишь электростатически, анион будет способен накапливаться у поверхности и изменять адсорбционное равновесие ионов Н+ и ОН- в (ТНЗ). До адсорбции А-должно соблюдаться равенство ГH+ = ГOH-, а после адсорбции ГH+ > ГOH-, так как адсорбция Н+ должна увеличиваться пропорционально ГA-, а адсорбция ОН- уменьшается. Поэтому для восстановления условия (ТНЗ) ГH+ = ГOH- необходимо повысить концентрацию ионов ОН- в растворе, т.е. повысить рН. Если определяется электрокинетический потенциал, то можно характеризовать изоэлектрическую точку (ИЭТ), которая будет иметь обратную от рассмотренной выше зависимость от рН. Действительно, если адсорбируются специфически ионы А-, то для восстановления z-потенциала потребовалось бы увеличить адсорбцию ионов Н+, что возможно в случае снижения рН. Аналогично можно объяснить и специфическую адсорбцию катионов.
Сдвиг ТНЗ и ИЭТ в разных направлениях - очень характерный критерий специфической адсорбции. По величине сдвига ТНЗ или ИЭТ можно даже оценить количество специфически адсорбированных ионов. Значения ИЭТ определяются электрокинетическими методами, а ТНЗ – потенциометрическим титрованием.
3. Проявлением лиотропных рядов при коагуляции гидрофобных коллоидов или при изменении электрокинетического потенциала при прочих равных условиях. Например, порог коагуляции уменьшается при переходе от иона Li+ к Сs+. В последнем случае специфичность адсорбции определяется способностью к гидратации ионов, что влияет на расстояние, на которое они способны приближаться к поверхности. При этом интенсивность специфического взаимодействия ионов с твердой поверхностью определяется именно различием в приближении к поверхности и изменением гидратных оболочек.
Строго говоря, теорию Штерна следует считать в определенной степени качественной теорией строения двойного слоя, так как в ней имеется неопределенность схематичного распределения заряда на диффузионную и адсорбционную части. Кроме того, Штерн использовал теорию адсорбции Ленгмюра, что накладывает дополнительные ограничения и не может исчерпывающе объяснить распределение заряда в двойном слое.
Вместе с тем теория Штерна объяснила обращение знака z-потенциала, что невозможно было сделать с привлечением теории Гуи-Чепмена. Поправка на специфическую адсорбцию позволяет также скорректировать завышенную величину заряда диффузного слоя, рассчитанную по теории Гуи-Чемпена.