Координата реакции
КООРДИНАТА РЕАКЦИИ, величина, характеризующая изменение многоатомной системы в процессе ее хим. превращ. из реагентов в продукты р-ции. Определение координаты реакции тесно связано с топографией поверхности потенциальной энергии (ППЭ) U (qi), к-рая является ф-цией N внутр. координат системы qi (i=1,2, ..., N), определяющих взаимное расположение атомных ядер, т. е. конфигурацию системы. Реагентам и продуктам на ППЭ соответствуют минимумы с конфигурациями (совокупностями координат) q'={q'1,q'2,...,q'N} и q''={q''1, q''2,..., q''N}, активированному комплексу -седловая точка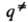
= {
,
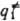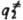
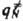}. Кривая, проходящая через эти три точки, наз. путем р-ции и определяется как путь скорейшего спуска из конфигурации 
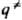в конфигурации q' и q: (рис. 1). При таком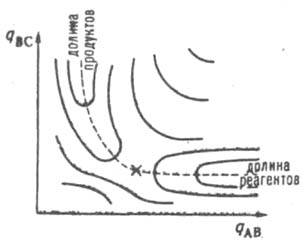
Рис. 1. Поверхность потенциальной энергии хим. р-ции А+ВС:АВ+С. Крестом обозначена седловая точка, пунктиром - путь р-ции.
определении путь р-ции часто называют путем минимальной энергии. Путь р-ции состоит из двух ветвей, одна из к-рых соответствует дну долины, ведущей из минимума, отвечающего реагентам, в точку перевала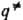 
, а другая-дну долины, ведущей из 
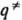в минимум, отвечающий продуктам. Координата реакции определяется как длина дуги s(q,q') на кривой пути р-ции, отсчитанная от начальной точки q' до любой точки q, лежащей на этой кривой. В точке перевала координата реакции 
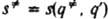, а в минимуме, отвечающем продуктам, координата реакции s''=s(q:,q'). Для нек-рых целей удобно пользоваться безразмерной координатой реакции а: 0[а= s/s:[1.
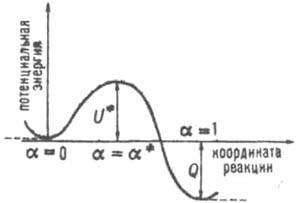
Рис. 2. Сечение поверхности потенциальной энергии вдоль пути р-ции. Реагентам и продуктам соответствуют минимумы при а=0 и а=1 (два изомера в случае изомеризации). Если долине реагентов или продуктов соответствуют дв" мол. фрагмента со свободным относит. движением, минимумы вырождаются в горизонтальные асимптотич. полупрямые (показаны пунктиром).
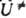, тепловой эффект р-ции Q и положение а№ вершины барьера на К- р. (ур-ния Поляки - Семенова, Брёнстеда, Маркуса, постулат Хаммонда и др.). Вудворда - Хофмана правила обычно выводят из корреляц. диаграмм, характеризующих изменения энергетич. уровней хим. системы при ее переходе от исходного состояния реагентов к продуктам вдоль предполагаемого пути р-ции, сохраняющего определенные элементы симметрии системы.
Уточнение и развитие концепции координаты реакции связано с проблемами динамики элементарного акта хим. р-ции. Во-первых, описанный выше выбор кривой пути р-ции как пути кратчайшего спуска из седловой точки в долины реагентов и продуктов на ППЭ неоднозначен. Он зависит от выбора внутр. координат системы qi. Однозначный (инвариантный) выбор модифицирует определение пути р-ции таким образом, что получаемая кривая в любой системе координат представляет собой одну и ту же последовательность геом. конфигураций q={q1, q2, .... qN} системы. Координата реакции, определенная на инвариантном пути р-ции, наз. собственной координатой реакции. Во-вторых, вводится понятие кривизны пути р-ции К=dy/ds, где s - собственная координата реакции, g=g(s) - угол между направлением касательной к инвариантной кривой пути р-ции и нек-рым заданным фиксир. направлением (напр., осью х, рис. 3а). Для описания дина ми ч. эволюции системы удобно перейти от внутр. координат qi к спец. криволинейным координатам - естеств. координатам. Одной из них является собственно координата реакции s. а остальные, наз. поперечными координатами, отсчитываются вдоль нормалей к пути р-ции в каждой его точке. Поперечные координаты локально являются координатами нормальных колебаний (нормальными колебат. модами), для к-рых равновесные положения лежат на пути р-ции, а формы и частоты изменяются с
изменением s. В естеств. координатах записывается гамильтониан системы (гамильтониан пути р-ции), позволяющий наглядно интерпретировать динамику элементарного акта процесса.
Динамич. взаимодействие между собственной координатой реакции и поперечными координатами в осн. определяется величиной К. В области поворота пути р-ции, где кривизна велика (рис. 3, а), происходит обмен энергией между поступательными (вдоль собственной координаты реакции) и колебательными движениями и создается неравновесная заселенность уровней поперечных колебат. степеней свободы. Если пренебречь кривизной пути р-ции и сопутствующими динамич. эффектами, то движение вдоль координаты реакции оказывается независимым от поперечных колебаний. Эта модель хим. процесса наз. адиабатической, она лежит в основе активированного комплекса теории.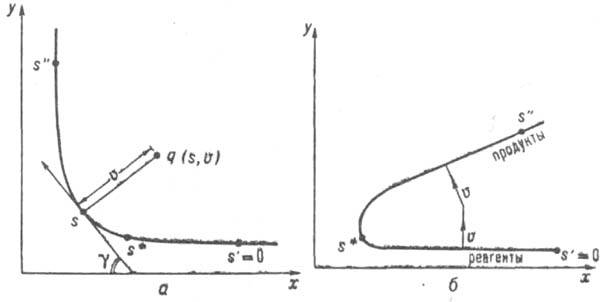
Рис. 3. Двухмерные схемы естественных координат р-ции: a - при малой кривизне пути р-ций. v поперечная колебат. координата, ортогональная пути р-ции. Точка q на плоскости ху (конфигурация системы) м. 6. описана в координатах s, v. Угол g определяет направление касательной к пути р-ции в каждой его точке; б - при большой кривизне пути р-ции. Переход из долины реагентов в долину продуктов вдоль колебат. координаты v показан стрелками.
Концепция координаты реакции не может быть универсальной и применимой к любым хим. процессам. Так, в системах с очень большой кривизной пути р-ции описание динамики элементарного акта в естественных координатах реакции неудовлетворительно. Возникает возможность прямых переходов из долины реагентов в долину продуктов не вдоль собственной координаты реакции, а вдоль поперечных координат (рис. 3,б), к-рые невозможно учесть в гамильтониане пути р-ции. Они имеют место, напр., при туннельных р-циях обмена легкого атома типа R1Н+R2:R1+R2H (см. Туннельный эффект в химии).
===
Исп. литература для статьи «КООРДИНАТА РЕАКЦИИ»: Базилевский М. В., Рябой В. М., Поверхности потенциальной энергии, в Сб.: Проблемы квантовой химии, т. 2, М., 1989.
Страница «КООРДИНАТА РЕАКЦИИ» подготовлена по материалам химической энциклопедии.