4.3. Политропный процесс

Политропным процессом называется процесс, все состояния которого удовлетворяются условию:

P· nⁿ = Const, (4.24)

где n – показатель политропы, постоянная для данного процесса.

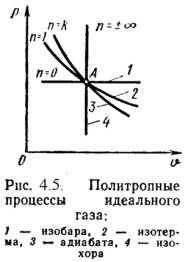
Изобарный, изохорный, изотермический и адиабатный процессы являются частными случаями политропного процесса (Рис.4.5):

при n = ± ¥ n = Const, (изохорный),

n = 0 P = Const, (изобарный),

n = 1 T = Const, (изотермический),

n = l P· n= Const, (адиабатный).

Работа политропного процесса определяется аналогично как при адиабатном процессе:

l = R·(T₁ – T₂) / (n – 1); (4.25)

l = R·T₁·[1 – (n ₁/ n ₂) ^n-1] /(n – 1); (4.26)

l = R·T₂·[1 – (P₂/P₁) ^{(n-1)/ n}] /(n – 1). (4.27)

Теплота процесса:

q = c_n ·(T₂ – T₁), (4.28)

где c_n = c_v ·(n - l)/(n – 1) – массовая теплоемкость (4.29)

политропного процесса.

 Предыдущая страница | Следующая страница

СОДЕРЖАНИЕ