Изображение молекул углеводов на плоскости

Хотя уже пещерные художники умели несколькими штрихами создавать адекватные образы явлений внешнего мира, проблема двухмерного изображения трехмерных объектов актуальная и по сей день. Вот, например, как столкнулся с ней шестилетний Антуан Сент-Экзюпери: «Я много раздумывал о полной приключений жизни джунглей и тоже нарисовал цветным карандашом свою первую картинку… Я показал свое творение взрослым и спросил, не страшно ли им. – Разве шляпа страшная? – возразили мне. А это была совсем не шляпа. Это был удав, который проглотил слона. Тогда я написовал удава изнутри, чтобы взрослым было понятнее. Им ведь всегда все нужно объяснять».

Из опыта автора «Маленького принца» мы видим, что есть два пути изображения объекта: подробное и схематическое. Первое технически сложно и мало годится для повседневности, второе удобно, но для его понимания требуется некоторое воображение. Для самого художника последнее ограничение не было существенным – он ведь много размышлял о своем предмете, прежде чем взялся за карандаш.

Молекулы сахаров – существенно трехмерные объекты. Но это еще не все. Гораздо важнее и менее тривиально, что у них нет никаких элементов симметрии, которые позволили бы изобразить их на бумаге в двух измерениях, без существенной потери информации. Это не бензол, имеющий плоскость симметрии и позволяющий без большого ущерба забыть об одной из пространственных координат и уверенно манипулировать на бумаге с плоским шестиугольником.

Выше мы пользовались проекцией Фишера. Она точно отражает относительную конфигурацию ассиметрических центров, но ничего не говорит (хуже того, говорит весьма искаженно) об истинном расположении атомов в пространстве. И уж совсем неудобной становится при изображении циклических структур. Отнюдь не случайно, формулы 17 и 18 имеют такой уродливый вид. Поэтому Хеуорс, один из классиков химии углеводов (который явно много размышлял о своем предмете), предложил повсеместно применяемые и по сей день так называемые перспективные формулы сахаров.

Если вы хотите подробно рассмотреть кольцо с камнем, вы вряд ли станете смотреть на него сбоку – исчезнет ощущение объемности и формы кольца. И не будете смотреть вдоль его оси – плохо виден камень. Скорее всего, вы посмотрите на него под некоторым углом – тогда и форма не ускользнет, и камень хорошо виден. Точно так же поступают (мысленно, разумеется) с циклической молекулой сахара при ее изображении по Хеуорсу.

Правило простое: обращенную к наблюдателю часть цикла на рисунке помещают снизу, а от наблюдателя – наверху. При этом заместители автоматически расположатся над или под линиями, очерчивающими цикл. Обычно (хотя и не всегда) атом кислорода, входящий в цикл, помещают в правом верхнем углу (для пираноз) или наверху (для фураноз). Так, например, b- D-глюкопираноза описывается формулой 19, а b- D-глюкофураноза – формулой 20. Все ясно и наглядно. Нужно только помнить, что связи заместителей при каждом из углеродных атомов цикла, например H-C и C-OH, не лежат на самом деле на одной прямой, как изображается на рисунке, а составляют часть тетраэдрической системы связей центрального углеродноо атома, т.е. угол H-C-OH не равен 180 ° , а близок к 109,5 °

Формулы Хеуорса ясны и удобны, но еще достаточно сложны и мало годятся для скорописи. Поэтому их обычно упрощают и схематизируют. Прежде всего отказываются от символов углеродных атомов цикла. Так получаются формулы 21 и 22. Затем убирают жирные линии, выделяющие приближенную к наблюдателю часть цикла. И, наконец, не изображают атомы водорода и их связи. Так приходят к формулам 23 и 24 – уже не «популярным», а тем самым, которые встречаются в любой вполне профессиональной статье или книге по химии сахаров.

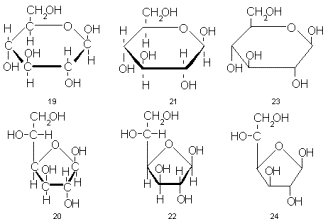
Надо ли доходить до такой степени схематизации, где углерод кажется трехвалентным, а части атомов вообще нет на рисунке? Заглянем на несколько десятков страниц вперед и подумаем, сколькопонадобится места и времени для изображения приведенных там структур формулами типа 19 и 20. Ответ станет ясен. В дальнейшем нам иногда придется прибегать к еще более схематичным изображениям, концентрируя внимание читателей на наиболее существенных особенностях обсуждаемых структур. К слову сказать, усложнение объекта неизбежно ведет к схематизации символики и языка (это общая тенденция всей науки). Важно только не скатиться к вульгаризации. Сравним для примера две структурные формулы октанола-1, одна из которых написана по всем школьным правилам структурных формул (25), а другая так, как становится обычным в современных работах по органической химии (26). Последняя формула при всей ее схематичности даже богаче информацией, чем первая, так как отражает наиболее характерное расположение атомов этого соединения в пространстве: плоский зигзаг.

Насыщенные шестичленные циклы (в нашем случае пиранозы) на самом деле не плоские. Чтобы валентные углы атомов, входящих в цикл мало отклонялись от наиболее энергетически выгодных – тетраэдрических – углов (109 ° 28’), молекула вынуждена принимать форму зигзага, замкнутого в цикл. Есть два типа таких зигзагов, обеспечивающих строго тетраэдрическиеуглы между связями атомов в шестичленном цикле. Один из них, отвечающий обычно минимуму энергии (и, следовательно, реализующийся предпочтительно), называется креслом. Для глюкозы такое кресло, выполненное в духе проекции Хеуорса, представлено формулой 27.

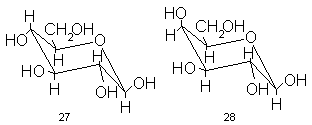
Эта формула очень близка к реальному расположению атомов глюкозы в реальном пространстве, и потому весьма богата информацией. Что же можно в ней усмотреть в первую очередь? Три атома цикла расположены над, а три других – под средней плоскостью, проходящей через центры всех шести связей, образующих цикл. Эта плоскость – основа геометрии кресла. Все пять CH-связей в цисле ориентированы перпендикулярно этой плоскости: параллельно оси цикла и друг другу.

Такие заместители называют аксиальными (от слова axis- ось). Все же гидроксильные группы глюкозы и CH ₂ OH-группа расположены вблизи плоскости цикла (точнее, их связи с циклом образуют с этой плоскостью углы около 30 ° ). Такие заместители называют экваториальными. Теперь видно, что пиранозный цикл в глюкозе охвачен, именно по экватору, почти равномерным кольцом из гидроксильных групп. А в галактозе, например, эта равномерность уже нарушена: гидроксил при С-4 занимает аксиальное положение и его химические свойства существенно отличны от свойств гидроксила при С-4 в глюкозе и всех остальных гидроксилов в галактозе (см. формулу 28).

Обратите внимание, какой контраст составляют эти заключения с теми, которые можно было бы вывести на проекции Фишера (ср. формулы 9 и 10). Так, может показаться, что в глюкозе гидроксил при С-3 стоит особняком, а остальные «скучены» по одну сторону молекулы, тогда как в галактозе, кажется, что гидроксилы при С-3 и С-4 (слева от оси формулы 10) сходны между собой и отличны от остальных. На основании формул типа 27 и 28, так называемых конформационных формул, можно, не прибегая к эксперименту, достаточно обоснованно предсказать множество химических и физических особенностей вещества. Сравнение формул 27 и 28 позволяет, например, оценить относительные скорости окисления глюкозы и галактозы периодатом (IO ₄ ^- ) и даже в общих чертах ход кинетической кривой этой реакции для галактозы, оценить относительное поведение этих сахаров при хроматографии на бумаге, предсказать характерные особенности спектров ядерного магнитного резонанса и даже высказать достаточно обоснованные предположения о том, почему именно глюкоза, а не какой-либо иной моносахарид занимает доминирующее положение в углеводном обмене любой живой системы.

Таким образом, конформационные формулы максимально информативны и приближены к реальности. Казалось бы, ими и нужно пользоваться. Однако именно в их детальности и заключается некоторая слабость.Дело в том, что они отражают не только структуру молекулы, т.е. ту единственную последовательность ковалентных связей атомов, которую молекула сохраняет, пока соединение остается самим собой. Конформационные формулы, помимо этого, отражают одну из тех форм, которые молекула принимает в пространстве, изгибаясь и деформируясь без разрыва ковалентных связей. Для данной молекулы таких форм (так называемых конформаций) в некоторых пределах может быть бесчисленное множество, и мы далеко не всегда знаем, какую же из этих конформаций принимает обсуждаемая молекула в действительности. В случае глюкозы и галактозы мы уверенно (и вполне обоснованно) приписали им конформации 27 и 28. Однако это далеко не всегда можно сделать с такой же уверенностью. Поэтому, когда предпочтительная конформация молекулы известна, или когда хотят подчеркнуть те или иные пространственные особенности молекулы, пользуются конформационными формулами. Если же нет оснований приписать соединению определенную конформацию или если нет необходимости акцентировать внимание на конформации, обычно пользуются формулами Хеуорса типа 23 или 24.

Предыдущая страница | Следующая страница

СОДЕРЖАНИЕ