11.2. Основные законы теплового излучения
Закон Планка. Интенсивности излучения абсолютно черного тела Isl и любого реального тела Il зависят от температуры и длины волны.
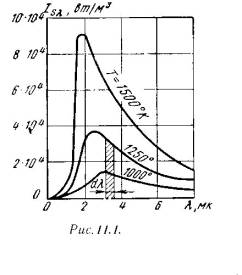
Абсолютно черное тело при данной температуре испускает лучи всех длин волн отl = 0 до l = ¥. Если каким-либо образом отделить лучи с разными длинами волн друг от друга и измерить энергию каждого луча, то окажется, что распределение энергии вдоль спектра различно.
По мере увеличения длины волны энергия лучей возрастает, при некоторой длине волны достигает максимума, затем убывает. Кроме того, для луча одной и той же длины волны энергия его увеличивается с возрастанием температуры тела, испускающего лучи (рис.11.1).
Планк установил следующий закон изменения интенсивности излучения абсолютно черного тела в зависимости от температуры и длины волны:
Isl = с1 l-5 / (ес/(lТ) – 1) , (11.5)
где е - основание натуральных логарифмов; с1 = 3,74*10-16 Вт/м2; с2 = 1,44*10-2 м*град; l - длина волны, м; Т - температура излучающего тела, К.
Из рис.11.1 видно, что для любой температуры интенсивность излучения Isl возрастает от нуля (при l=0) до своего наибольшего значения, а затем убывает до нуля (при l=¥). При повышении температуры интенсивность излучения для каждой длины волны возрастает.
lms = 2,9 / T. (11.6)
С увеличением температуры lms уменьшается, что и следует из закона.
Пользуясь законом смещения Вина, можно измерять высокие температуры тел на расстоянии, например, расплавленных металлов, космических тел и др.
Закон Стефана-Больцмана. Планк установил, что каждой длине волны соответствует определенная интенсивность излучения, которая увеличивается с возрастанием температуры. Тепловой поток, излучаемый единицей поверхности черного тела в интервале длин волн от l до l + dl, может быть определен из уравнения
dEs = Isl*dl . (11.7)
Элементарная площадка на рис.11.1, ограниченная кривой Т = const, основанием dl l ординатами l и l + dl (Isl) определяет количество лучистой энергии dEs и называется лучеиспускательной способностью абсолютно черного тела для длин волн dл. Вся же площадь между любой кривой Т = const и осью абсцисс равна интегральному излучению черного тела в пределах от l = 0 до l = ¥ при данной температуре.
Подставляя в уравнение (11.7) закон Планка и интегрируя от от l = 0 до l = ¥, найдем, что интегральное излучение (тепловой поток) абсолютно черного тела прямо пропорционально четвертой степени его абсолютной температуры (закон Стефана-Больцмана).
Es = Сs (Т/100)4 , (11.8)
где Сs = 5,67 Вт/(м2*К4) - коэффициент излучения абсолютно черного тела
Отмечая на рис.11.1 количество энергии, отвечающей световой части спектра (0,4—0,8 мк), нетрудно заметить, что оно для невысоких температур очень мало по сравнению с энергией интегрального излучения. Только при температуре солнца ~ 6000К энергия световых лучей составляет около 50% от всей энергии черного излучения.
Все реальные тела, используемые в технике, не являются абсолютно черными и при одной и той же температуре излучают меньше энергии, чем абсолютно черное тело. Излучение реальных тел также зависит от температуры и длины волны. Чтобы законы излучения черного тела можно было применить для реальных тел, вводится понятие о сером теле и сером излучении. Под серым излучением понимают такое, которое аналогично излучению черного тела имеет сплошной спектр, но интенсивность лучей для каждой длины волны Il при любой температуре составляет неизменную долю от интенсивности излучения черного тела Isl, т.е. существует отношение:
Il/ Isl = e = const. (11.9)
Величину e называют степенью черноты. Она зависит от физических свойств тела. Степень черноты серых тел всегда меньше единицы.
Большинство реальных твердых тел с определенной степенью точности можно считать серыми телами, а их излучение — серым излучением. Энергия интегрального излучения серого тела равна:
Е = e*Es = С* (Т/100)4 . (11.10)
Лучеиспускательная способность серого тела составляет долю, равную е от лучеиспускательной способности черного тела.
Величину С = e*Es называют коэффициентом излучения серого тела. Величина С реальных тел в общем случае зависит не только от физических свойств тела, но и от состояния поверхности или от ее шероховатости, а также от температуры и длины волны. Значения коэффициентов излучения и степеней черноты тел берут из таблиц.
Таблица 11.1
Степень черноты полного нормального излучения
для различных материалов
| Наименование материала | t ,°С | e |
| Алюминий полированный | 50—500 | 0,04—0,06 |
| 50 | 0,1 | |
| Железо листовое оцинкованное, блестящее | 30 | 0,23 |
| Жесть белая, старая | 20 | 0,28 |
| Золото полированное | 200 - 600 | 0,02—0,03 |
| Латунь матовая | 20-350 | 0,22 |
| Медь полированная | 50—100 | 0,02 |
| Никель полированный | 200—400 | 0,07—0,09 |
| Олово блестящее | 20—50 | 0,04—0,06 |
| Серебро полированное | 200—600 | 0,02—0,03 |
| Стальной листовой прокат | 50 | 0,56 |
| Сталь окисленная | 200—600 | 0,8 |
| Сталь сильно окисленная | 500 | 0,98 |
| Чугунное литье | 50 | 0,81 |
| Асбестовый картон | 20 | 0,96 |
| Дерево строганое | 20 | 0,8—0,9 |
| Кирпич огнеупорный | 500—1000 | 0,8—0,9 |
| Кирпич шамотный | 1000 | 0,75 |
| Кирпич красный, шероховатый | 20 | 0,88—0,93 |
| Лак черный, матовый | 40—100 | 0,96—0,98 |
| Лак белый | 40—100 | 0:8—0,95 |
| Масляные краски различных цветов . . . | 100 | 0,92—0,96 |
| Сажа ламповая | 20—400 | 0,95 |
| Стекло | 20—100 | 0,91—0,94 |
| Эмаль белая | 20 | 0,9 |
Закон Кирхгофа. Для всякого тела излучательная и поглощательная способности зависят от температуры и длины волны. Различные тела имеют различные значения Е и А. Зависимость между ними устанавливается законом Кирхгофа:
Е = Еs*А или Е /А = Еs = Еs/Аs = Сs*(Т/100)4 . (11.11)
Отношение лучеиспускательной способности тела (Е) к его погло-щательной способности (А) одинаково для всех серых тел, находящихся при одинаковых температурах и равно лучеиспускательной способности абсолютно черного тела при той же температуре.
Из закона Кирхгофа следует, что если тело обладает малой поглощательной способностью, то оно одновременно обладает и малой лучеиспускательной способностью (полированные металлы). Абсолютно черное тело, обладающее максимальной поглощательной способностью, имеет и наибольшую излучательную способность.
Закон Кирхгофа остается справедливым и для монохроматического излучения. Отношение интенсивности излучения тела при определенной длине волны к его поглощательной способности при той же длине волны для всех тел одно и то же, если они находятся при одинаковых температурах, и численно равно интенсивности излучения абсолютно черного тела при той же длине волны и температуре, т.е. является функцией только длины волны и температуры:
Еl / Аl = Il / Аl = Еsl = Isl = f (l ,T). (11.12)
Поэтому тело, которое излучает энергию при какой-нибудь длине волны, способно поглощать ее при этой же длине волны. Если тело не поглощает энергию в какой-то части спектра, то оно в этой части спектра и не излучает.
Из закона Кирхгофа также следует, что степень черноты серого тела е при одной и той же температуре численно равно коэффициенту поглощения А:
e = Il / Isl = Е/ Еsl = C / Csl = А . (11.13)
Закон Ламберта. Излучаемая телом лучистая энергия распространяется в пространстве по различным направлениям с различной интенсивностью. Закон, устанавливающий зависимость интенсивности излучения от направления, называется законом Ламберта.
Закон Ламберта устанавливает, что количество лучистой энергии, излучаемое элементом поверхности dF1 в направлении элемента dF2, пропорционально произведению количества энергии, излучаемой по нормали dQn, на величину пространственного угла dщ и cosц, составленного направлением излучения с нормалью (рис.11.2):
d2Qn = dQn*dw*cosj. (11.14)
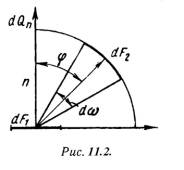
Следовательно, наибольшее количество лучистой энергии излучается в перпендикулярном направлении к поверхности излучения, т. е. при (j = 0). С увеличением j количество лучистой энергии уменьшается и при j = 90° равно нулю. Закон Ламберта полностью справедлив для абсолютно черного тела и для тел, обладающих диффузным излучением при j = 0 - 60°.
Для полированных поверхностей закон Ламберта неприменим. Для них лучеиспускание при угле j будет большим, чем в направлении, нормальном к поверхности.


