Кинетика ферментативных реакций

Кинетика ферментативной реакции (т. е. зависимость скорости реакции от ее условий) определяется в первую очередь свойствами катализатора, вследствие чего она значительно сложнее, чем кинетика некаталитических реакций (см. с. 28).

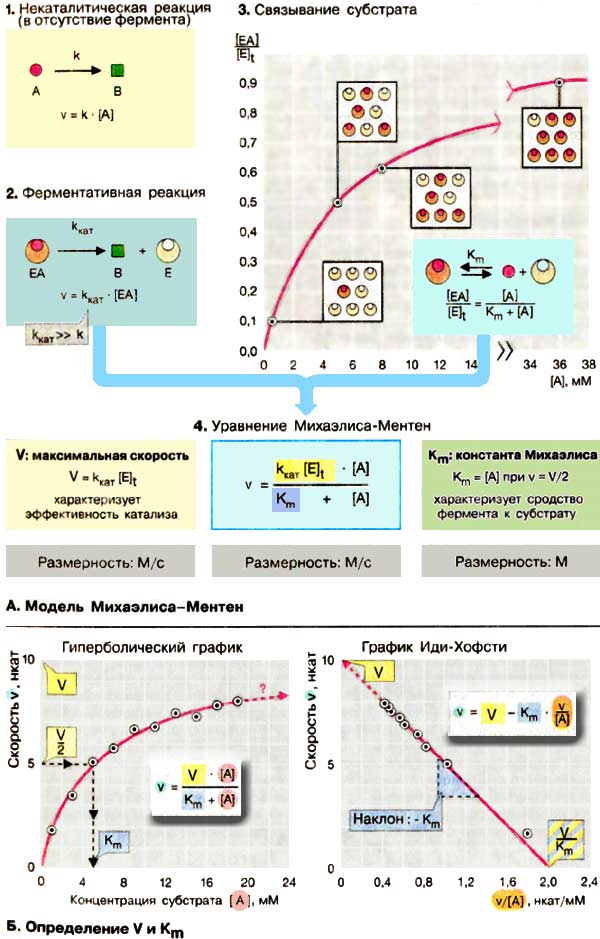
А. Модель Михаэлиса-Ментен

Полный математический анализ ферментативной реакции приводит к сложным уравнениям, не пригодным для практического применения. Наиболее удобной оказалась простая модель, разработанная в 1913 г. Она объясняет характерную гиперболическую зависимость активности фермента от концентрации субстрата (1) и позволяет получать константы, которые количественно характеризуют эффективность фермента.

Модель Михаэлиса-Ментен исходит из того, что вначале субстрат А образует с ферментом E (З) комплекс, который превращается в продукт В намного быстрее, чем в отсутствие фермента. Константа скорости k_кат (2) намного выше, чем константа некаталитической реакции k. Константу k_кат называют еще «числом оборотов» поскольку она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 с. Согласно этой модели, активность фермента определяется долей комплекса EA от общей концентрации фермента [E] _t , т. е., отношением [EA] / [E] _t (З). С целью упрощения модель предполагает, что E, А и ЕА находятся в химическом равновесии согласно закону действующих масс (см. с. 24), что дает в итоге для диссоциации комплекса EA уравнение:

[E][A]/[EA] = K_m Поскольку [E] _t = [E] + [EA],

[EА] = [E] _t [А]/(К_m + [А])

Из v = k_кат[EA] (2) и предыдущего выражения получают уравнение Михаэлиса-Ментен (4).

Уравнение содержит две величины (два параметра), которые не зависят от концентрации субстрата [A], но характеризуют свойства фермента: это произведение k_кат[E] _t , соответствующее максимальной скорости реакции V при высокий концентрации субстрата, и константа Михаэлиса К_m , характеризующая сродство фермента к субстрату. Константа Михаэлиса численно равна той концентрации субстрата [A]. при которой ν достигает половины максимальной величины V (если v = V/2, то [A] / (К_m + [A]) = 1/2, т. е. K_m = [А]). Высокое сродство фермента к субстрату характеризуется низкой величиной К_m и наоборот,

Модель Михаэлиса-Ментен основывается на нескольких не совсем реальных допущениях, таких, как необратимое превращение EA в E + В, достижение равновесия между E, A и EA, отсутствие в растворе других форм фермента, кроме E и EA. Только при соблюдении этих гипотетических условий K_m соответствует константе диссоциации комплекса, а k_кат — константе скорости peакции EA → E + В.

Б. Определение V и К_m

В принципе V и К_m можно определить по графику зависимости v от [A] (рис. слева). Так как v асимптотически достигает V с возрастанием концентрации субстрата [A], то затруднительно получить надежную величину V и К_m (рис. слева) путем экстраполяции.

Для удобства расчетов уравнение Михаэлиса-Ментен можно преобразовать так, чтобы экспериментальные точки лежали на прямой. При одном из таких графических преобразований в так называемом графике Иди-Хофсти (pиc. справа) строят график зависимости v от v/[A]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует V, а тангенс угла наклона равен -K_m. Такой графический подход дня определения V и К_m также не оптимален. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью вычислительной техники.

• ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ КИНЕТИКА - химическая энциклопедия
• Кинетика ферментативных реакций - Биологическая химия